WYKŁAD 4

WYZNACZNIK MACIERZY

Każdej macierzy kwadratowej A można w sposób jednoznaczny przyporządkować liczbę, zwaną jej wyznacznikiem. Będziemy go oznaczali symbolami det [a_ij], det A lub A

Definicję wyznacznikiem podajemy na dwa sposoby rekurencyjne.

DEFINICJA (WYZNACZNIKA MACIERZY)

• det [a₁₁] = a₁₁ dla n = 1

• det A = a₁₁(-1)¹⁺¹ detA₁₁ + a₁₂(-1)¹⁺²detA₁₂ + … + a_1n(-1)¹⁺ⁿ detA_1n dla n≥2 ,

gdzie A_ij oznacza macierz powstałą przez skreślenie wiersza o numerze i oraz kolumny o numerze j.

METODY OBLICZANIA WYZNACZNIKA

Macierz drugiego stopnia

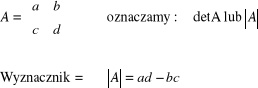
Macierz trzeciego stopnia

Jeżeli mamy macierz trzeciego stopnia:

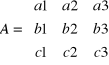
to wyznacznik takiej macierzy możemy wyznaczyć na trzy sposoby:

Pierwszy sposób (metoda Sarrusa):

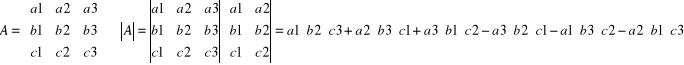
Drugi sposób:

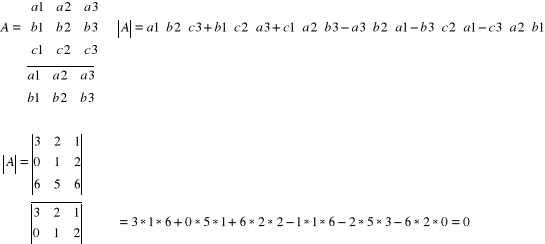
Macierz której wyznacznik jest równy 0 („zero”) nazywa się macierzą osobliwą.

Trzeci sposób:

.

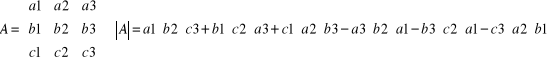
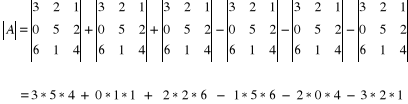
Bardzo użytecznym narzędziem w liczeniu wyznaczników stopnia większego niż 3 jest reguła Laplace'a, której podanie poprzedzone zostanie definicją dopełnienia algebraicznego macierzy.

DEFINICJA

Dopełnieniem algebraicznym A*_ij elementu aij nazywamy iloczyn wyrażenia (-1) ^i+j oraz wyznacznika macierzy powstałej przez skreślenie wiersza o numerze i oraz kolumny o numerze j.

TWIERDZENIE (Reguła Laplace'a). Niech A = [a_ij] będzie macierzą kwadratową stopnia n≥2 oraz k≥1, l≤n. Wyznacznik macierzy A jest równy sumie iloczynów elementów k -tego wiersza (l-tej kolumny) i ich dopełnień, co zapisujemy:

det A = a_k1A*_k1 + a_k2A*_k2 + …+ a_knA*_kn (rozwinięcie wyznacznika wg elementów k-tego wiersza)

det A = a_1lA*_1l + a_2lA*_2l + …+ a_nlA*_nl (rozwinięcie wyznacznika wg l-tej kolumny)

Ponieważ obliczanie wyznaczników stopnia większego niż 3 jest z reguły procesem długotrwałym, praco- i czasochłonnym, dlatego aby uprościć ten proces należy zapoznać się z następującymi twierdzeniami:

TWIERDZENIE 1

Jeżeli dowolny wiersz (kolumna) wyznacznika składa się z samych zer, to wyznacznik ten jest równy 0.

TWIERDZENIE 2

Jeżeli w wyznaczniku dwa wiersze (kolumny) są proporcjonalne, to ten wyznacznik jest równy 0.

TWIERDZENIE 3

Jeżeli do dowolnego wiersza (kolumny) dodamy inny wiersz(kolumnę) to wartość wyznacznika nie ulegnie zmianie.

TWIERDZENIE 4

Jeżeli w wyznaczniku przestawimy dwa dowolne wiersze (kolumny) to znak wyznacznika zmieni się na przeciwny.

TWIERDZENIE 5

Wyznacznik macierzy kwadratowej A jest równy wyznacznikowi macierzy do niej transponowanej A^T.

DEFINICJA (MACIERZY TRANSPONOWANEJ)

Niech będzie dana macierz A = [a_ij] _mxn. Macierz A^T mająca postać A^T = [a_ji]_nxm nazywamy macierzą transponowaną do macierzy A.

PRZYKŁAD

Znaleźć macierz transponowaną do macierzy A.

1 0

A = -1 0

2 2

Rozwiązanie. Zamieniając wiersze na kolumny oraz kolumny na wiersze otrzymujemy

A^T = 1 -1 2

0 3 2

dopisujemy dwie kolumny

dopisujemy dwa rzędy

---