Rozkład dwumianowy - Bernoulliego
Rozkład dwumianowy polega na przeprowadzeniu n jednakowych, niezależnych doświadczeń, z których każde może zakończyć się „sukcesem” z prawdopodobieństwem p lub „porażką” z prawdopodobieństwem q=1-p. Prawdopodobieństwo pojawienia się sukcesu jest jednakowe w każdym z kolejnych doświadczeń. Zmienną losową w tym eksperymencie jest zdarzenie polegające na pojawieniu się k liczby sukcesów w próbach, przy czym k<0, n>.
![]()
gdzie:
k = 1, 2, 3, ..., n - liczba wystąpienia „sukcesów”
n - liczba doświadczeń
p - prawdopodobieństwo wystąpienia sukcesów
Dystrybuanta zmiennej losowej o rozkładzie dwumianowym ma postać:
![]()
Wartość oczekiwana w rozkładzie dwumianowym:
![]()
Wariancja w rozkładzie dwumianowym:
![]()
Przykład
Pewna firma posiada pięć jednakowych komputerów pracujących niezależnie od siebie. Prawdopodobieństwo tego, że w ciągu dnia roboczego komputer ulegnie awarii wynosi 0,1. Zakładamy, że awarię usuwa się dopiero następnego dnia. Jaki jest rozkład liczby komputerów ulegających awarii w ciągu dnia roboczego i jakie jest prawdopodobieństwo tego, że w ciągu dnia awarii ulegną więcej niż dwa komputery?
![]()
Prawdopodobieństwa odpowiadające poszczególnym wartościom (realizacjom zmiennej losowej X) są następujące:
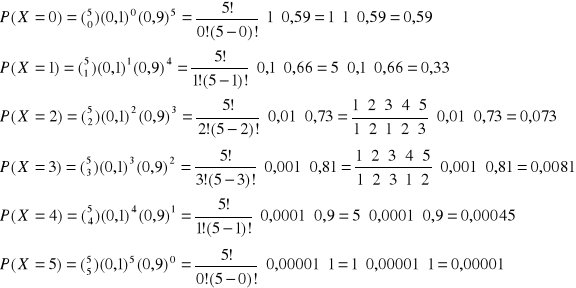
Rozkład zmiennej losowej X można przedstawić w następującej postaci:

Dystrybuanta zmiennej losowej X przyjmuje więc postać:

Korzystając z wyznaczonej funkcji prawdopodobieństwa i dystrybuanty obliczymy prawdopodobieństwo tego, że w ciągu dnia roboczego ulegną awarii więcej niż dwa komputery. Można to zrobić na dwa sposoby:
P(X > 2) = 1 - P(X ≤ 2) = 1 - F(2) = 1 - 0,99144 = 0,00856
P(X>2) = P(X=3) + P(X=4) + P(X=5) = 0,0081 + 0,00045 + 0,00001 = 0,00856
Oczekiwana (średnia) liczba komputerów ulegających awarii w ciągu dnia roboczego wynosi:
E(X) = 5 * 0,1 = 0,5
Wariancja jest równa:
D2(X) = 5 * 0,1 * 0,9 = 0,45
Odchylenie standardowe wynosi:
D(X) = √0,45 = 0,67
Zadania
Z akt firmy ubezpieczeniowej wynika, że 30 % posiadaczy polis, którzy przekroczyli 50 lat, zgłasza roszczenia w ciągu jednego roku. Wybrano losowo pięciu posiadaczy polis mających powyżej 50 lat. Jakie jest prawdopodobieństwo, że: 1) roszczenia zgłosi dokładnie dwóch posiadaczy, 2) nie więcej niż trzech posiadaczy zgłosi roszczenia, 3) co najmniej trzech z nich zgłosi roszczenia w ciągu nadchodzącego, 4) mniej niż trzech posiadaczy zgłosi roszczenia. Wyznacz średnią oraz odchylenie standardowe w odpowiednim rozkładzie.
Na osiedlu znajdują się 4 sklepy spożywcze. Prawdopodobieństwo zamknięcia każdego z nich z powodu choroby pracowników wynosi 0,4. Oblicz prawdopodobieństwo, że: 1. Będzie otwarty tylko jeden sklep, 2. Otwartych będzie co najwyżej dwa sklepy, 3. Otwartych będzie co najmniej 2 sklepy.
Prawdopodobieństwo wylosowania orła w rzucie monetą wynosi 0.5. Wyznacz i przedstaw na wykresie rozkład prawdopodobieństwa p(k) i dystrybuantę F(k), gdzie k=0,1,...,10 jest liczbą wystąpienia orła w dziesięciu próbach. Jakie jest prawdopodobieństwo, że w 10 próbach: (1) 6 razy wypadnie orzeł, (2) co najmniej 6 razy wypadnie orzeł, (3) co najwyżej 6 razy wypadnie orzeł.
Stwierdzono, że 40% Polaków korzysta z ROR. Jakie jest prawdopodobieństwo, że spośród 10 klientów robiących zakupy: (1) 5 klientów zapłaci czekiem, (2) nie mniej niż 2 zapłaci czekiem, (3) żaden nie zapłaci czekiem, (4) wszyscy zapłacą czekiem. (5) Oblicz średnią liczbę klientów płacących czekiem. Sporządź wykresy rozkładu prawdopodobieństwa i dystrybuanty.
W kontroli jakości partia wyrobów zostaje zaakceptowana jako dobra tylko wtedy, gdy liczba sztuk wadliwych nie przekracza ustalonej z góry wartości w stosunku do liczebności całej partii. Zakładamy, że w dużej partii występuje 20 % sztuk wadliwych. Pobrano próbę liczącą 20 sztuk. Procedura kontrolna przewiduje zaakceptowanie partii wyrobów, gdy nie więcej niż 2 sztuki okażą się wadliwe. Jakie jest prawdopodobieństwo, że partia wyrobów nie zostanie zaakceptowana?
![]()
Wyszukiwarka