Uniwersytet Medyczny w Łodzi

Wydział fizjoterapii

Laboratorium z Biofizyki

Statystyka

Magdalena Tobiasz

Grupa 6

Zespół 2

6 III 2006

Średnia arytmetyczna z serii pomiarów - liczba równa sumie wartości wszystkich pomiarów podzielonej przez ilość tych pomiarów. Można to zapisać wzorem:

n - liczba dokonanych pomiarów
<A> średnia arytmetyczna ze wszystkich pomiarów
A_i - wartość zmierzona pomiaru o numerze i

Zapis w formie rozpisanej:

Odchylenie standardowe - klasyczna miara zmienności, obok średniej arytmetycznej najczęściej stosowane pojęcie statystyczne.Dla skończonych populacji obliczamy je ze wzoru:

gdzie x_i to kolejne wartości cechy w populacji, μ to wartość oczekiwana, N to liczba elementów w populacji.

Odchylenie standardowe w populacji można estymować odchyleniem standardowym z próby losowej, oznaczanym przez s. Odpowiedni wzór ma postać:

gdzie x_i to kolejne wartości cechy elementów próby losowej,
to średnia arytmetyczna z próby, zaś n to liczba elementów w próbie.

Odchylenie standardowe ma szereg własności, które powodują, że jest to miara bardzo przydatna w statystyce opisowej. Przede wszystkim jest ono wyrażone w tych samych jednostkach co wartości cechy.

Przedział ufności jest to obszar:

,

w którym z zadanym prawdopodobieństwem 1-a, zawiera się estymowany parametr rozkładu m. Prawdopodobieństwo 1-a nazywamy poziomem ufności, najczęściej wykorzystujemy wartości a = 10%, 5% lub 1%.

Błędy pomiarowe -ograniczona dokładność narzędzia pomiarowego powoduje, że wskazanie narzędzia różni się od wartości prawdziwej wielkości mierzonej. Różnicę między tymi wartościami nazywa się błędem pomiaru.

Błędy dzielimy na:

Błędy systematyczne są to błędy, które przy wielu pomiarach tej samej wartości określonej wielkości, wykonywanych w tych samych warunkach, są stałe lub zmieniają się wg określonego prawa wraz ze zmianą warunków. Błędy systematyczne stałe mają tą sama wartość i znak przy każdym pomiarze. Powstają np. przy użyciu narzędzi pomiarowych w warunkach różnych od warunków odniesienia , przy użyciu miernika z przesuniętym położeniem zerowym lub błędnie wykonaną podziałką. Błędy systematyczne zmienne maja różne wartości w funkcji czasu lub w funkcji innej wielkości (np. mierzonej). Na przykład mierzony prąd nagrzewa sprężyny wytwarzające moment zwrotny miernika, a to powoduje wzrost wychylenia wskazówki tego miernika. Wykrycie błędów systematycznych jest bardzo trudne. Wielokrotne powtarzanie pomiarów nie umożliwia ich wykrycia ani wyeliminowania. Istnienie błędów systematycznych można stwierdzić w wyniku zastosowania innej metody pomiarowej lub zastosowanie innego narzędzia pomiarowego.

Błędy przypadkowe są to błędy zmieniające się w sposób nieprzewidywalny (losowy), zarówno co do znaku, jak i wartości bezwzględnej , przy powtarzaniu pomiarów tej samej wielkości mierzonej w warunkach praktycznie niezmiennych. Błędów przypadkowych nie można usunąć z wyników pomiarów przez dodanie poprawek , ponieważ wartości tych poprawek są niezmienne. Na podstawie serii pomiarów i rachunku prawdopodobieństwa ustala się granice w których znajdują się błędy przypadkowe ( przedział niepewności końcowego wyniku pomiaru).

Błędy grube są to błędy wynikające z nieprawidłowego wykonania pomiarów np. z użycia uszkodzonego przyrządu, omyłkowo włączonego zakresu pomiarowego, omyłkowego odczytania wyniku. Wyniki pomiarowe obarczone błędami grubymi na ogół nie są uwzględniane przy obliczaniu końcowego wyniku pomiaru.

Błąd bezwzględny D jest różnicą miedzy wynikiem pomiaru x a wartością prawdziwą
wielkości mierzonej v, czyli
D= x-v
Błąd bezwzględny D, zawsze wyrażany w jednostkach wielkości mierzonej, ma konkretny znak: plus (+) lub minus (-).
Wartość prawdziwa v jest w praktyce nieznana. W pomiarach można ją zastąpić względnie dokładnym przybliżeniem, tzn. wartością poprawną xp, otrzymaną za pomocą wzorcowego narzędzia pomiarowego.
Błąd bezwzględny D, lecz ze znakiem przeciwnym , nazywa się poprawką
p = - D
Dodając algebraicznie poprawkę p do wartości x uzyskanej z pomiarów, otrzymuje
się wynik poprawiony, równy wartości poprawnej
xp = x + p

Błąd względny d jest to stosunek błędu bezwzględny D do wielkości mierzonej v, czyli
lub wyrażonego w procentach
Ponieważ D << x, v » xp » x, wiec przy obliczeniu stosuje się przybliżenie
Błąd względny umożliwia porównanie dokładności przyrządów pomiarowych różnych typów o różnych zakresach.

Rozkład normalny:

Mamy do czynienia z rozkładem normalnym wtedy, gdy pomiar pewnej wielkości, mającej wartość μ zakłócany jest bardzo dużą liczbą niezależnych czynników, z których każdy z prawdopodobieństwem ½ powoduje odchylenie o niewielką wartość ±ε.

μ

μ-ε μ+ε

μ-2ε μ μ+2ε

Gęstość prawdopodobieństwa rozkładu normalnego standaryzowanego

Rozkład ten oznaczany jest także jako N(0, 1). Wartość oczekiwana i wariancja rozkładu normalnego standaryzowanego

Rozkład Studenta: Zmienną losową t Studenta definiujemy wzorem

gdzie Z jest zmienną losową standaryzowaną N(0, 1), a U zmienną losową o rozkładzie chi kwadrat i k stopniach swobody.

Gęstość prawdopodobieństwa rozkładu Studenta

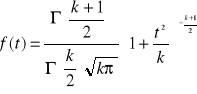
gdzie Γ jest funkcją gamma Eulera, a parametr k nazywa się liczbą stopni swobody.

Rozkład Studenta jest identyczny z rozkładem Gaussa N(0, 1) dla k=∞ i staje się coraz bardziej spłaszczony dla malejących k. Wartość oczekiwana rozkładu Studenta jest równa zero, wariancja jest równa k/(k-2).

Tablice Studenta zawierają zazwyczaj tak zwane wartości krytyczne t_n,α zmiennej losowej Studenta, zdefiniowane wyrażeniem

---