Transformacja Lorentza

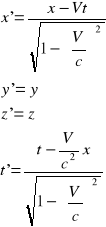
z S' do S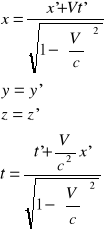

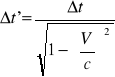
wydłużenie czasu

transformacja długości:

w układzie gdzie sztaba się porusza

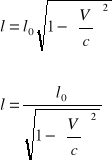
skrócenie długości

Transformacja prędkości

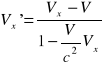
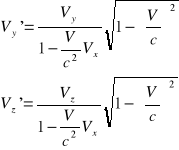
Dynamika relatywistyczna

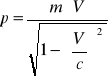
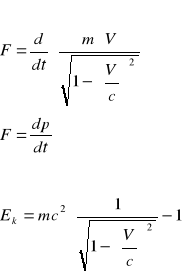
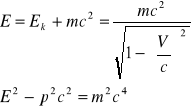
Czterowektor, czteropęd

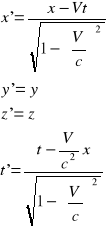
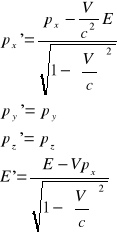
Równania Maxwella

Do opisu zjawisk elektromagnetcznych zachodzących w przyrodzie, zgodnie z teorią Maxwella, stosujemy wektorowe pola, elektryczne e(t,r) i pole indukcji magnetycznej, które spełniają poniższy układ równań różniczkowych:

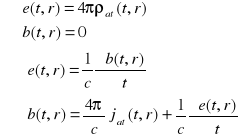
Równania w formie (1)-(4) odnoszą się do pól w skali atomowej, o których możemy myśleć że są średnimi odpowiednich pól kwantowych, wiążąc między sobą pole elektryczne e(t,r) z polem indukcji magnetycznej b(t,r) , a także ze żródłami tych pól które zadane są zadane gęstościami ładunku elektrycznego
i strumienia prądu elektrycznego
. Pomimo licznych eksperymentów nie udało się odkryć monopli magnetycznych, dlatego łamiemy symetrię między polami e(t,r) i b(t,r) i pole magnetyczne jako spełniające równanie (2), staje się polem bezżródłowym; dalsze tego konsekwencje obserwujemy w równaniu (3) w którym nie występują prądy magnetyczne rozumiane jako strumienie monopoli magnetycznych. Prostym rachunkiem, można z równań Maxwella (1)-(4) wyprowadzić równanie ciągłości

Aby się o tym przekonać, należy skorzystać z pierwszego równania Maxwella (1) a następnie z równania (4), co nam daje

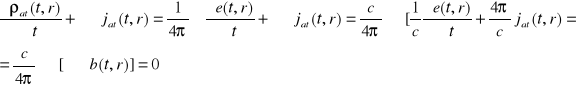
Jeśli scałkujemy równanie (5) po objętości
otoczonej powierzchnią
, a następnie skorzystamy z twierdzenia Gaussa, otrzymamy

Ten ostatni wynik (6) pokazuje, że w istocie rzeczy, równanie ciągłości (5) jest konsekwencją zasady zachowania ładunku.

6. Elektrodynamika

prawo Coulomba

wektor natężenia pola elektrycznego

F₀ - siła elektrostatyczna działająca na ładunek próbny ze strony N ładunków qi

równanie ruchu cząstki

prawo Gaussa

(strumień wektora natężenia pola elektrycznego)

strumień kuli

wektor indukcji magnetycznej

Φ = q

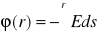
potencjał elektryczny

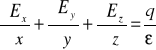
równanie Poissona

diwergencja:

divD = q