ESTYMACJA
Przedział ufności dla średniej
Zadanie 1
W grupie 900 losowo wybranych pracowników przedsiębiorstwa średnia liczba dni nieobecności w pracy wynosiła 30, a odchylenie standardowe 3 dni.
Przyjmując współczynnik ufności na poziomie 0,9 oszacować średnią absencję w pracy wśród ogółu pracowników.
Jak zmieni się przedział ufności, jeżeli przyjmiemy współczynnik ufności na poziomie 0,95.
Zadanie 2
Na podstawie wielokrotnych obserwacji ustalono, że rozkład czasu dojazdu do pracy osób zatrudnionych w sklepach stołecznych jest rozkładem normalnym. W celu oszacowania nieznanej średniej w tym rozkładzie wylosowano niezależnie 17 - elementową próbę pracowników. Średni czas dojazdu w tej próbie wynosił 40 minut a odchylenie standardowe stanowiło połowę czasu średniego. Przyjmując współczynnik ufności 0,95, oszacować metodą przedziałową średni czas dojazdu do pracy ogółu pracowników.
Przedział ufności dla wskaźnika struktury (procentu)
Zadanie 3
Oszacować przedziałowo jaka część młodzieży szkół licealnych pali papierosy, jeżeli w próbie wybranej w losowaniu niezależnym, liczącej 1000 uczniów, 220 osób paliło papierosy. Przyjąć współczynnik ufności 0,9.
Przedział ufności dla wariancji i odchylenia standardowego
Zadanie 4
Wymiary 6 losowo wybranych detali, wyrażone w mm, kształtowały się następująco: 6,3; 5,9; 6,2; 5,8; 5,7; 6,1. Przyjmując założenie, że rozkład wymiarów ogółu produkowanych detali jest normalny, przy współczynniku ufności równym 0,9 oszacować nieznane odchylenie standardowe wymiarów ogółu produkowanych detali.
Zadanie 5
Przy badaniu wysokości wynagrodzeń w przemyśle odzieżowym w 1993 r. wylosowano 200 pracowników. Na podstawie wyników próby otrzymano średnią płacę na poziomie 77,8 oraz odchylenie standardowe równe 15,5. Przyjmując współczynnik ufności na poziomie 0,95 oszacować nieznane odchylenie standardowe w rozkładzie wynagrodzeń ogółu pracowników przemysłu odzieżowego.
Wyznaczanie niezbędnej liczby pomiarów do próby
Zadanie 6
Jak liczną próbę należy wylosować z partii liczącej 2000 sztuk rur stalowych, aby oszacować przeciętną średnicę rur z błędem maksymalnym nie przekraczającym 1,2 mm, jeżeli z poprzednich ustaleń wynika, że wariancja średnicy rur wynosiła 2,8 ![]()
? Przyjąć współczynnik ufności na poziomie 0,9.
Zadanie 7
W losowo wybranej próbie 100 studentów UMK 40 osób mieszkało na stałe w Toruniu. Przyjmując współczynnik ufności na poziomie 0,95:
Oszacować przedziałowo udział studentów mieszkających na stałe poza Toruniem wśród ogółu studentów.
Określić, o ile osób należy zwiększyć powyższą próbę, aby dwukrotnie wzrosła precyzja oszacowania.
Estymacja punktowa
Zadanie 8
Wylosowano 500 turystów polskich powracających do kraju z pobytów krótkookresowych i zbadano ich ze względu na wartość przewożonych legalnie towarów spożywczych (bez alkoholi). Okazało się, że średnia arytmetyczna wartość towarów wynosi 36,74 zł na jednego turystę, przy odchyleniu standardowym równym 5,26 zł. Oszacować metodą punktową wartość oczekiwaną.
WERYFIKACJA HIPOTEZ STATYSTYCZNYCH
PARAMETRYCZNE TESTY ISTOTNOŚCI
Test dla wartości średniej populacji
Zadanie 1
Zbadano w 81 wylosowanych zakładach pewnej gałęzi przemysłowej koszty materiałowe przy produkcji pewnego wyrobu i otrzymano średnią 540 zł oraz odchylenie standardowe 150 zł. Na poziomie istotności równym 0,05 zweryfikować hipotezę, że średnie koszty materiałowe przy produkcji tego wyrobu wynoszą 600 zł.
Zadanie 2
Na losowo dobranej próbie 10 samochodów marki „Skoda” przeprowadzono badanie zużycia benzyny po przejechaniu trasy 100 km. Okazało się, że średnie zużycie benzyny dla tej próby samochodów wynosiło 7,1l przy odchyleniu standardowym 0,9l. Jednocześnie wiadomo, że norma fabryczna zużycia benzyny po przebyciu trasy 100 km wynosi 7,7l. Czy można twierdzić, że rzeczywiste zużycie benzyny jest mniejsze niż wynosi norma fabryczna. Weryfikację przeprowadzić dla poziomu istotności ![]()
oraz ![]()
.
Zadanie 3
Czas montowania elementu w automatycznej pralce bębnowej jest zmienną losową o rozkładzie normalnym. Norma techniczna przewiduje na tę czynność 6 min, natomiast wśród jej wykonawców istnieje pogląd, że ten normatywny czas jest zbyt krótki. Należy sprawdzić to przypuszczenie przy założeniu, że odchylenie standardowe czasu montowania wynosi 1min 30s. Obliczono, że w grupie 25 robotników średni czas montowania wynosi 6 min 20s. Przyjąć poziom istotności 0,05.
Test dla dwóch średnich
Zadanie 4
Wylosowana do badań budżetów rodzinnych próba 120 rodzin zamieszkałych w Toruniu dała średnią 450zł miesięcznych wydatków na mieszkanie oraz odchylenie standardowe 120zł. Natomiast losowa próba 100 rodzin zamieszkałych w Bydgoszczy dała średnią 420zł miesięcznych wydatków na mieszkanie oraz odchylenie standardowe 150zł. Przyjmując poziom istotności 0,05 zweryfikować hipotezę o jednakowych średnich wydatkach na mieszkanie w Toruniu i Bydgoszczy.
Zadanie 5
W wyniku ewidencji dziennej sprzedaży dwóch rodzajów zegarków na rękę szwajcarskiej firmy w wybranych 20 dniach roboczych ustalono:
zegarki tradycyjne ![]()
![]()
zegarki z dodatkowymi funkcjami ![]()
![]()
Czy na poziomie istotności 0,1 można przyjąć, że średnia dzienna sprzedaż zegarków tradycyjnych jest większa niż zegarków z dodatkowymi funkcjami.
Test dla wskaźnika struktury (procentu)
Zadanie 6
Sondaż opinii publicznej na temat frekwencji oczekiwanej na wyborach wykazał, że w losowo wybranej grupie 2500 osób 1600 zamierza uczestniczyć w głosowaniu. Czy na poziomie istotności równym 0,05 można przyjąć, że 60% ogółu osób zamierza wziąć udział w wyborach?
Test dla dwóch wskaźników struktury
Zadanie 7
Do produkcji wprowadzono tańszy surowiec. Pobrano próbę losową 200szt. wyrobów produkowanych z droższego surowca, wśród których było 180 szt. pierwszego gatunku. W wylosowanej próbie 300 szt. produkowanych z tańszego surowca wyrobów takich było 230 szt. Czy zmiana surowca wpłynęła na obniżenie się jakości produkcji? Przyjąć poziom istotności 0,05.
Test dla wariancji populacji generalnej
Zadanie 8
Średnie odchylenie od normy pracochłonności przy produkcji wyrobu pojedynczego robotnika powinno wynosić 7,9 min/wyrób. Wylosowano 20 robotników, których odchylenie standardowe pracochłonności wynosiło 8,4 min/wyrób. Przyjmując poziom istotności 0,01 zweryfikować hipotezę o równości faktycznego i zakładanego odchylenia standardowego.
Test dla dwóch wariancji
Zadanie 9
W celu porównania regularności uzyskiwanych wyników sportowych dwu oszczepników, wylosowano 20 wyników rzutu oszczepem zawodnika A i 16 wyników zawodnika B. Otrzymano dla zawodnika A odchylenie standardowe wynoszące 2,65m, a dla zawodnika B wynoszące 4,80m. Na poziomie istotności 0,05 sprawdzić hipotezę o większej regularności wyników zawodnika A.
NIEPARAMETRYCZNE TESTY ISTOTNOŚCI
Test zgodności
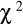
Zadanie 1
W pewnym mieście wylosowano niezależnie 500 rodzin i zbadano miesięczne zużycie energii elektrycznej u każdej z nich. Otrzymano rozkład:
Zużycie energii w kWh |
35 - 45 |
45 - 55 |
55 - 65 |
65 - 75 |
75 - 85 |
Liczba rodzin |
70 |
100 |
140 |
110 |
80 |
Na poziomie istotności 0,01 zweryfikować hipotezę, że rozkład zużycia energii elektrycznej przez te rodziny jest normalny.
Zadanie 2
Ewidencja liczby awarii urządzeń technicznych w zakładzie produkcyjnym w ciągu kolejnych 160 dni roboczych dostarczyła następujących informacji:
Liczba awarii |
0 |
1 |
2 |
3 |
4 |
Liczba dni |
35 |
57 |
36 |
21 |
11 |
Czy zakładając prawdopodobieństwo popełnienia błędu pierwszego rodzaju na poziomie 0,1 można uznać powyższy rozkład za zgodny z rozkładem Poissona z ![]()
?
Test zgodności
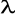
- Kołmogorowa
Zadanie 3
Poniższe zestawienie zawiera informację o łącznej liczbie punktów uzyskanych przez studentów studiów dziennych z czterech kolejnych prac kontrolnych ze statystyki:
Liczba punktów |
poniżej 65 |
65 - 70 |
71 - 75 |
76 - 80 |
81 - 85 |
85 i więcej |
Liczba studentów |
10 |
20 |
40 |
50 |
40 |
40 |
Korzystając z testu ![]()
- Kołmogorowa, należy zweryfikować hipotezę, że powyższy rozkład jest zgodny z rozkładem normalnym o wartości oczekiwanej i odchyleniu standardowym równym odpowiednio 78 oraz 9 punktów.
Test zgodności Kołmogorowa - Smirnowa
Zadanie 4
W zakładach produkujących wyrób M zostały wprowadzone zmiany w strukturze organizacyjnej. W celu stwierdzenia, czy reorganizacja spowodowała zmianę kosztów jednostkowych wytwarzania produktu M zbadano próbę 200 zakładów przed reorganizacją oraz 100 zakładów po reorganizacji i zbadano w nich koszty jednostkowe, otrzymując poniższe rozkłady empiryczne:
Koszty w zł |
2,5-3,5 |
3,5-4,5 |
4,5-5,5 |
5,5-6,5 |
6,5-7,5 |
7,5-8,5 |
8,5-9,5 |
Liczba zakł. przed reorg. |
5 |
10 |
35 |
80 |
50 |
10 |
10 |
Liczba zakł. po reorg. |
8 |
10 |
12 |
30 |
20 |
15 |
5 |
Przyjmując poziom istotności 0,01 zweryfikować hipotezę, że rozkłady kosztów jednostkowych przed i po reorganizacji są identyczne.
4
Wyszukiwarka