DOLNOŚLĄSKIE MECZE MATEMATYCZNE 2004/05

KATEGORIA: SZKOŁY PODSTAWOWE

RUNDA PÓŁFINAŁOWA

MECZ I

1. Mam tyle samo braci co sióstr, a moja siostra ma dwa razy mniej sióstr niż braci. Ile chłopców i ile dziewcząt jest w naszej rodzinie?

2. W Bajdocji nazywają dobrą każdą liczbę naturalną, która jest zapisana przy pomocy różnych cyfr, których iloczyn jest równy 360. Jaka jest największa dobra liczba naturalna?

3. Badacz roślin pustynnych, profesor Kaktus zamierza odbyć podróż przez Saharę drogą, która zabiera 11 dni. Jeden człowiek może unieść racje żywności tylko na 8 dni. Dzienna racja żywieniowa kosztuje 5 klipów. Profesor może wynająć dowolną liczbę tragarzy, którzy za każdy dzień pracy otrzymują wynagrodzenie 20 klipów. Jeśli zginą podczas wykonywania obowiązków służbowych, pracodawca musi wypłacić rodzinie 2000 klipów. Profesor dysponuje ograniczonymi funduszami na badania. Jaki jest najniższy koszt wyprawy?

4. Ile kwadratów jest na szachownicy 6×6?

5. Zuza ma urodziny w mikołajki. Napisała list do św. Mikołaja i zapytała, ile ma on lat. List schowała pod poduszkę, a następnego dnia znalazła tam odpowiedź: „Mam tyle lat, ile Ty liczysz sobie miesięcy”. Zuza pomyślała chwilę i wykrzyknęła: „To razem mamy 91 lat!”. Ile lat ma Zuza?

6. Ile jest różnych trójkątów prostokątnych o polu 2004 i przyprostokątnych naturalnej długości?

7. Rada miasta Pacanowa postanowiła ujednolicić miejskie rejestracje samochodowe. Pod głosowanie mają pójść dwa projekty: w jednym numer ma się składać z 4 liter, po których następują 3 cyfry, a w drugim z grupy 3 liter i 4 cyfr, ale grupa liter może być na początku lub na końcu numeru. W pierwszym projekcie dodatkowo w grupie liter musi na początku wystąpić P (jak Pacanów). Pacanów rozwija się bardzo dynamicznie. Jak powinni zagłosować radni, żeby numerów wystarczyło dla większej liczby mieszkańców?

8. Ile różnych łamanych (rozróżniamy kształt i położenie) może zakreślić piłka rzucana kolejno co tyle samo osób w gronie 12 dziewcząt stojących w równych odstępach na obwodzie koła?

9. Czterdzieści dwie osoby bawiły się na balu karnawałowym. Podczas zabawy zauważono, że:

- jedna pani tańczyła z siedmioma panami,

- druga pani tańczyła z ośmioma panami,

- trzecia pani tańczyła z dziewięcioma panami

itd., a ostatnia pani tańczyła ze wszystkimi panami obecnymi na balu. Ile pań było na tym balu?

10. Odkryj zaszyfrowane działanie, wiedząc, że te same cyfry oznaczają te same litery, a różnym cyfrom odpowiadają różne litery: SOK + SKO = OKS.

DOLNOŚLĄSKIE MECZE MATEMATYCZNE 2004/05

KATEGORIA: SZKOŁY PODSTAWOWE

RUNDA PÓŁFINAŁOWA

MECZ II

1. Liczbę 2005 przedstawiono jako sumę czterech liczb naturalnych, o których wiadomo, że pierwsza jest mniejsza lub równa drugiej, druga mniejsza lub równa trzeciej, a trzecia mniejsza lub równa czwartej. Ile najwyżej może wynosić pierwsza z tych liczb?

2. Zegar ratuszowy wybija godzinę ósmą w ciągu 8 sekund. W jakim czasie wybija południe?

3. W jaki sposób wlać dokładnie litr wody do butelki o nieznanej pojemności (ale trochę większej niż 1 litr) przy pomocy dwóch naczyń o pojemnościach 12 i 7 litrów? Wodę czerpiemy z kranu i w razie potrzeby wylewamy ją do zlewu.

4. Dobry piechur przechodzi 100 metrów w czasie, gdy zły przechodzi 60. Dobry piechur staje na starcie, a zły dostaje fory i wyprzedza dobrego o 100 metrów. Po ilu metrach od startu dobry piechur go dogoni?

5. Ile kwadratów można zobaczyć w prostokącie 8×6 podzielonym na jednostkowe kwadraty?

6. „Kto gwizdał? ”- zdenerwowany nauczyciel zapytał o to swoich czterech uczniów, z których tylko jeden właśnie zagwizdał. Udzielili oni następujących odpowiedzi:

Jacek: “To Marcin!”, Marcin: „To Darek!”, Wojtek: „Nie ja gwizdałem!”, Darek: „Marcin kłamie!”. Nauczyciel wie, że jego uczniowie są kłamczuchami. W tym przypadku aż trzech skłamało i tylko jeden powiedział prawdę. Kto gwizdał, a kto powiedział prawdę?

7. Jaka jest 2005. cyfra rozwinięcia dziesiętnego ułamka
   ?

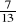
8. Bak był pełen benzyny. Przelano ją do trzech kanistrów. Do każdego z nich przelano tę samą całkowitą liczbę litrów. Okazało się, że w pierwszym kanistrze benzyna wypełniła
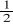
   jego objętości, w drugim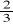
   , a w trzecim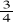
   . Przy jakiej najmniejszej objętości baku jest możliwa taka sytuacja, jeśli objętości baku i kanistrów wyrażają się całkowitymi liczbami litrów?

9. Cenę butów obniżono o 15%, a potem podwyższono o 10% i 2 złote. Obecnie cena butów to 39,40 zł. Jaka była cena butów przed obniżką, a jaka po obniżce?

10. Rada miasta Pacanowa postanowiła ujednolicić miejskie rejestracje samochodowe. Rajcy miejscy są bardzo przesądni. Uważają liczby nieparzyste za pechowe, a słowa - palindromy (które tak samo czyta się w przód i wspak) za chroniące przed złym urokiem. W głosowaniu postanowiono, że numery mają się składać z palindromu 3-literowego i następującej po nim 5-cyfrowej parzystej liczby palindromicznej. Dla ilu pojazdów wystarczy tych numerów?

DOLNOŚLĄSKIE MECZE MATEMATYCZNE 2004/05

KATEGORIA: SZKOŁY PODSTAWOWE

RUNDA PÓŁFINAŁOWA

MECZ III

1. Pies dostrzegł w odległości 60 m biegnącego kota i rozpoczął pościg. Skok psa ma długość 2 m, a skok kota 1 m. Pies oddaje dwa skoki w tym samym czasie, w jakim kot trzy. Czy pies dogoni kota? Jeśli tak, to po ilu metrach?

2. Podczas wigilijnej wieczerzy zebrała się cała rodzina. W ciszy złożyli sobie życzenia i zjedli tradycyjnie 12 potraw. Mały Antek nie mógł doczekać się rozdawania prezentów i stale spoglądał na stary ścienny zegar, bo mama mu powiedziała, że kolacja potrwa 4 godziny. Antek nie zna się jeszcze na zegarku, ale potrafi sprawnie liczyć do 20. Podczas kolacji policzył, że zegar wybił właśnie tyle razy i jeszcze dwa. O której godzinie rozpoczęła się kolacja?

3. Ile sześcianów jest w sześcianie 5×5×5 podzielonym na sześciany jednostkowe?

4. Rada miasta Pacanowa postanowiła ujednolicić numery rejestracyjne taksówek w mieście. Postanowiono, że na cześć burmistrza Marcina Raroga, który został właśnie wybrany na drugą kadencję, wszystkie numery mają zawierać 6 liter dających imię burmistrza lub jego anagram (słowo o przestawionych literach) i jedną cyfrę wstawioną w dowolne miejsca między tymi literami (na początku i na końcu też). Dla ilu taksówek wystarczy takich numerów?

5. W kryptarytmie AB თ A თ B  =  BBB zaszyfrowane są dwie jednocyfrowe liczby całkowite dodatnie, jedna liczba dwucyfrowa i jedna trzycyfrowa zapisane w układzie dziesiętnym. Różne litery zastępują różne cyfry, a różne cyfry zostały zastąpione przez różne litery. Znajdź A i B.

6. Liczby całkowite dodatnie nieprzekraczające czterdziestu czterech podzielono na dwa zbiory ze względu na parzystość. Następnie z każdego zbioru wybrano możliwie największy podzbiór, tak że sumy liczb w tych podzbiorach były równe. Ile elementów wybrano z każdego zbioru i jaka była suma wszystkich wybranych liczb?

7. 
   Wojtek skonstruował piramidę liczbową (patrz rys).

W pierwszym wierszu umieścił swoje ulubione liczby całkowite:

4, 7, 5. Następne pola wypełniał tak, że dodawał liczby

znajdujące się powyżej danej kratki i wpisywał w nią ostatnią

cyfrę otrzymanej sumy. Jeżeli powyżej kratki była tylko jedna

liczba, to przepisywał ją. Jaki będzie 2005. wiersz tej piramidy?

8. Liczba monet w kolekcji Janka jest większa od 300, a mniejsza od 350 oraz przy dzieleniu przez 15 daje resztę 9, a przy dzieleniu przez 8 - resztę 4. Ile monet jest w tej kolekcji?

9. W ciągu jednego miesiąca niedziela wypadła trzykrotnie w dniu parzystym. Jaki dzień tygodnia wypadł w 20. dzień tego miesiąca?

10. Liczba całkowita przy dzieleniu przez 10 daje k i reszty k (k≠0). Ile jest takich liczb?

.........

4 7 5

1 2

1 3 2

4 5

---