PJWSTK-MATEMATYKA DYSKRETNA 2001/02
1. Które z poniższych relacji binarnych ~ są relacjami równoważności:
Relacja ~ określona w zbiorze liczb całkowitych Z \ {0}:
Relacja ~ określona w zbiorze liczb całkowitych Z:
Rozważmy relację binarną w zbiorze liczb całkowitych Z:
x ~ y wttw x - y jest wielokrotnością 5.
Udowodnić, że ~ jest relacją równoważności. Ile klas abstrakcji ma ta relacja. Wskazać kilka elementów
Które z relacji przedstawionych w Zad 1 są relacjami częściowego porządku?
Rozważmy relację ~ w zbiorze R x R:
(a, b) ~ (c, d) wttw a3 c3 , b3 d3
Czy ~ jest relacją częściowego porządku, dlaczego?
Rozważmy zbiór liczb rzeczywistych R z relacją Znaleźć:
Zbuduj matrycę logiczną dla następującej formuły rachunku zdań:
Które z poniższych formuł są tautologiami rachunku zdań
Czy następująca reguła wnioskowania jest poprawna, dlaczego?:
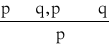
Zapisać w postaci formuły rachunku kwantyfikatorów następujące zdania:
Dla każdych liczb rzeczywistych x, y istnieje liczba rzeczywista z taka, że y < z oraz z < x
Istnieje liczba naturalna a taka, że b jest wielokrotnością a dla wszystkich liczb naturalnych b
Udowodnić indukcyjnie wzór
1 + 3 + 5 + ... + (2n+1) = (n+1)2
T. Lan Le E-mail: lan@ippt.gov.pl
![]()