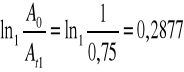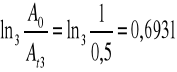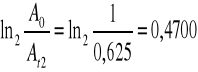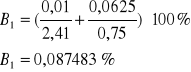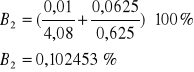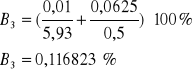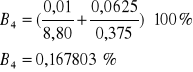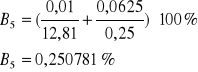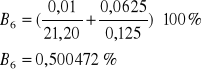Wyznaczenie współczynnika tłumienia i logarytmicznego dekrementu tłumienia.
At |
t1 [s] |
t2 [s] |
t3 [s] |
tśrednie [s] |
|
0,75 |
2,41 |
2,32 |
2,5 |
2,41 |
0,2877 |
0,625 |
3,91 |
4,07 |
4,25 |
4,08 |
0,4700 |
0,5 |
6 |
5,57 |
6,23 |
5,93 |
0,6931 |
0,375 |
8,84 |
8,59 |
8,96 |
8,80 |
0,9808 |
0,25 |
12,96 |
12,44 |
13,02 |
12,81 |
1,3863 |
0,125 |
21,03 |
20,69 |
21,87 |
21,20 |
2,0794 |
t1,t2,t3 - trzy kolejne pomiary czasu, dla dokładniejszych pomiarów
Obliczając czas średni wykorzystałem wzór ![]()
Obliczam zależność ![]()
Ao - amplituda początkowa
At - amplituda po czasie t
Przyjmuję początkowe wychylenie amplitudy oscyloskopu Ao = 1
Obliczenia zależności |
|
|
|
Obliczam względny błąd pomiarowy ze wzoru:
![]()
![]()
- niedokładność pomiaru czasu, która wynosi w moim przypadku 0,01 s gdyż stoper, którego używałem miał taką dokładność
![]()
- niedokładność pomiaru wychylenia amplitudy oscylatora, która wynosi 0,0625 gdyż z taką dokładnością byłem wstanie odczytać wartość z ekranu
Obliczenia błędów |
Wynik |
|
|
Błędy z obliczeń wyszły mi tak małe, że niemożliwością jest zaznaczyć je na wykresie.
Współczynnik tłumienia![]()
jest równy tangensowi nachylenia wykreślnej do osi poziomej. Średnia wartość współczynnika ![]()
, jest równa 0,658.
Okres drgań kamertonu T = ![]()
= 0,004 s
Logarytmiczny dekrement tłumienia:
![]()
Wnioski:
Z wyników błędów pomiarowych wynika, że przy małej wielkości amplitudy błąd pomiarowy jest większy natomiast przy dużych wychyleniach amplitudy błąd maleje, dzieje się tak, dlatego że przy małych wychyleniach dokładnie nie widać, kiedy amplituda przekracza skale odczytu. Tak, więc wraz z pomniejszeniem amplitudy dokładności wyników maleją
Wyszukiwarka
Podobne podstrony:
ruch harmoniczny1, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania), Cw
Data wykonania ćw, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania), Cw
sila termoelektryczna, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania),
LAB21, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania), Cw 21
CW6, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania), Cw 06
Badam zależność temperatury wrzenia wody od ciśnienia, Transport i Logistyka (AM) 1 (semestr I), Fiz
wyznaczanie ciepła właściego ciał stałych, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza la
Wyznaczanie ciepła skraplania i topnienia, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza la
CW 20, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania), Cw 20
Pomiary przeprowadzono dla trzech, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (r
bezwladnosc bryly sztywnej, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiąza
Cw06 1, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania), Cw 06
CW20, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania), Cw 20
obliczanie gestosci cieczy i cial stalych, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza la
sila termoelektryczna, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania),
LAB21, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania), Cw 21
Sprezyste ciala, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania), Labor
SPR F 7, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania), Laborki, Labo
więcej podobnych podstron