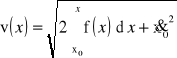Rozwiązania wybranych równań różniczkowych zwyczajnych
o stałych współczynnikach
Równanie typu:
![]()
Rozwiązanie:
![]()
gdzie:
x(t) - całka ogólna równania niejednorodnego,
x*(t) - całka ogólna równania jednorodnego,
x**(t) - całka szczególna równania niejednorodnego.
Tok rozwiązania
Rozwiązujemy równanie jednorodne
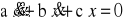
Postać całki ogólnej - x*(t) jest uzależniona od pierwiastków równania charakterystycznego:
![]()
gdzie:
r - parametr równania
Obliczamy wyróżnik równania charakterystycznego:
![]()
Jeżeli <0, to:
r1 = + i
r2 = - i
gdzie:
![]()
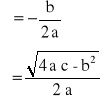
Wtedy:
![]()
gdzie:
C1, C2 - stałe. Jeżeli rozwiązujemy tylko równanie jednorodne, to wyznacza się je z warunków początkowych
Jeżeli =0, to:
![]()
wtedy:
![]()
gdzie:
C1, C2 - stałe.
Jeżeli >0, to:
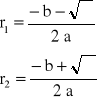
wtedy:
![]()
gdzie:
C1, C2 - stałe.
Wyznaczamy x** - całkę szczególną równania niejednorodnego
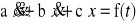
Funkcję x**(t) przewiduje się w postaci analogicznej do funkcji f(t), tzn.:
jeżeli: to:
![]()
![]()
![]()
![]()
gdzie:
A - stały parametr.
Parametr A ma taką wartość, że równanie:
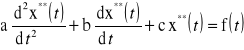
jest spełnione w każdej chwili czasu (dla każdego t).
Stałe C1 i C2, występujące w całce ogólnej równania niejednorodnego, wyznaczamy z warunków początkowych.
Równanie typu:
![]()
Równanie to rozwiązuje się poprzez dwukrotne całkowanie w przedziale (0,t). Po uwzględnieniu warunków początkowych:
![]()
otrzymuje się rozwiązanie w postaci:
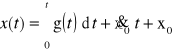
gdzie:
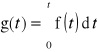
Równanie typu:
![]()
Po podstawieniu:
![]()
otrzymuje się równanie:
![]()
Rozwiązanie tego równania, po uwzględnieniu warunku początkowego:
![]()
ma postać:
![]()
Ostatecznie, po scałkowaniu powyższego równania i uwzględnieniu warunku początkowego:
![]()
otrzymuje się rozwiązanie w postaci:
![]()
Równanie typu:
![]()
(1)
Równanie to jest równaniem nieliniowym. Metodami stosowanymi w przypadku równań liniowych można je rozwiązać tylko wtedy, gdy poszukiwaną funkcją jest pochodna funkcji x(t), a więc np.: prędkość punktu materialnego:
![]()
Wtedy:
![]()
Równanie (1) ma więc postać:
![]()
czyli po rozdzieleniu zmiennych:
![]()
Po scałkowaniu i uwzględnieniu warunków początkowych:
![]()
otrzymuje się rozwiązanie w postaci: