WYZNACZANIE PRĘDKOŚCI DŹWIĘKU W METALU METODĄ KUNDTA

I. Wstęp:

Ze względu na sposób drgania cząstek fale dzielą się na podłużne i poprzeczne. W fali podłużnej kierunek drgań jest równoległy do kierunku rozchodzenia się, a w fali poprzecznej - prostopadły. Fala podłużna może rozchodzić się w każdym ośrodku, natomiast fala poprzeczna tylko w ciałach stałych. Źródłem fali jest drgające ciało wzbudzające drgania w otaczającym ośrodku.

Aparatura składa się z rury szklanej i pręta metalowego oraz tłoczka zamykającego drugi koniec rury. W czasie pomiaru musimy wytworzyć w pręcie drgania podłużne (wytworzą się tylko drgania o częstotliwości tonu podstawowego). Koniec pręta wchodzący do rury zaopatrzony jest w płytkę. Drgania pręta poprzez tą płytkę zostaną przekazane słupowi powietrza w rurze. Długość słupa powietrza w rurze można zmieniać za pomocą tłoczka, by spełnione były warunki rezonansu, wtedy również w słupie powietrza wytwarza się fala stojąca, w której rozkład węzłów i strzałkach przypomina n-tą harmoniczną. Węzły i strzałki tej fali uwidocznić można za pomocą pyłu korkowego. W obu środowiskach : pręcie i powietrzu rozchodzi się fala o tej samej częstotliwości f.

Aby powstał w rurze rezonans:

• częstotliwość tonu powstającego w pręcie:

• częstotliwość tonu powstającego w rurze:

• częstotliwość tonu pierwszego harmonicznego w rurze:

• drugiego:

• n-tego:

Zgodnie z warunkiem powstawania rezonansu:

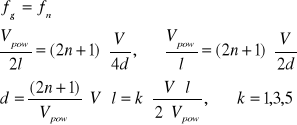
Przy przejściu fali akustycznej z ośrodka do ośrodka nie zmienia się częstotliwości fali

czyli:

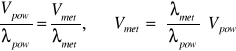
Ze wzoru Laplace'a na prędkość podłużnej fali sprężystej

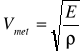
Moduł Younga mosiądzu

2. Obliczenia

Obliczamy prędkość dźwięku w mosiądzu ze wzoru:

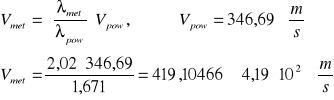
Moduł Younga dla mosiądzu wynosi:

mosiądzu

Obliczamy średnią długość fali akustycznej w powietrzu metodą regresji liniowej z

zależności:

przyjmujemy że x = n , y = 2a

x	1	2	3	4	5	6	7	8	9
y	18	37	55	74	92	111	129	148	166

Obliczamy długość fali w pręcie ze wzoru:

3. Analiza błędu

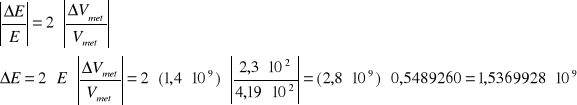
4. Zestawienie wyników

Prędkość dźwięku w mosiądzu wynosi

Moduł Younga wynosi:

---