Statystyka dla menedżerów

Cztery główne powody:

1. właściwie prezentować i opisać informacje (statystyka opisowa i informatyka)

2. wyciągnąć wnioski o licznych populacjach otrzymanych z próby (wnioskowanie statystyczne, statystyka matematyczna)

3. uzyskać wiarygodne prognozy i projekcje (analiza korelacji, tendencje rozwojowe, szeregi czasowe)

4. ulepszyć procesy, którymi się zajmują zawodowo (ciągłe doskonalenie zarządzania - total quality menagement)

Te cztery powody tworzą podstawę struktury i zawartości statystyki dla menedżerów, gdyby tym zagadnieniom poświęcić specjalne studia podyplomowe dla menedżerów.

Porównanie myślenia statystycznego i metod statystycznych

Wyszczególnienie	Myślenie statystyczne	Metody statystyczne
Ogólne podejście	Konceptualne	Techniczne
Zastosowanie	Uniwersalne	Ukierunkowane
Podstawowe wymagania	Wiedza	Dane
Logiczna kolejność	Naprowadzanie	Wzmocnienie

Wykorzystanie myślenia statystycznego:

• strategiczne → kierownictwo przedsiębiorstwa (dokąd zmierzamy)

• zarządzające → menedżerowie (zarządzanie procesami)

• operacyjne → pracownicy niższego szczebla (wykonywanie zleceń, monitorowanie)

Cztery elementy myślenia strategicznego:

1. Pojęcie procesu

2. Zrozumienie i radzenie sobie ze zmiennością

3. Zrozumienie i odpowiednie wykorzystanie narzędzi statystycznych

4. Systematyczne podejście do procesu ulepszania

Standaryzacja rozkładu normalnego o parametrach  i δ , tj. N (, δ)

A. Szukanie prawdopodobieństwa dla x<a

Korzystamy ze wzoru:

gdzie jest to kwantyl standaryzowanego rozkładu normalnego, tj. N (0,1), a  ( )

- prawdopodobieństwem z tablic rozkładu normalnego.

Przykład:

Dla przeciętnej  = 250 i odchylenia standardowego δ =20, wtedy prawdopodobieństwo dla wielkości mniejszej od 260, tj. x<260 dla kwantyla standaryzowanego rozkładu normalnego

= = 0,5

a z tablic rozkładu normalnego uzyskamy:  (0,5) = 0,6915

B. Prawdopodobieństwo dla zmiennej losowej w przedziale a<x<b

Przy standaryzacji korzystamy z podanych niżej przekształceń:

Przykład:

Dla przykładu podanego powyżej prawdopodobieństwo, że zmienna losowa znajdzie się w przedziale od 240 do 270, tj. 240<x<270 wyniesie:

P(240<x<270) = ( ) - ( ) =  (1,0) -  (-0,5) = 0,8413 - 0-385 = 0,5328

C. Prawdopodobieństwo dla zmiennej losowej większej od np. c, tj. x>c

korzystamy z drugiego aksjomatu Kołmogorowa, że P (x>x) + P (x<x) = 1, stąd otrzymamy:

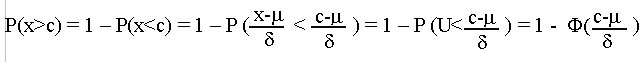
Przykład:

Dla przykładu [odanego powyżej prawdopodobieństwo, że zmienna losowa będzie większa od np. 255, tj. x> 255, obliczcamy ze wzoru:

P(x>255) = 1-P (x,255) = 1-P (U< )= 1 -  ( ) = 1 -  (-0,25) =

= 1 - 0,4013 = 0,5987

a-

δ

a-

δ

260 - 250

20

10

20

270 - 250

20

240 - 250

20

255 - 260

20

255 - 260

20

---