3. Kinematyka odwrotna

1. Dane na symbolach ogólnych:

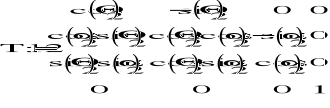
Macierze przekształceń z notacji D-H:

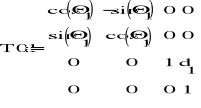
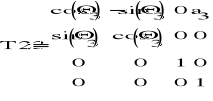
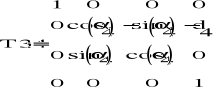
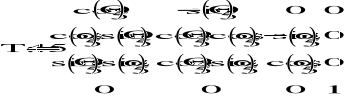
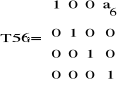
Do kinematyki odwrotnej potrzebna jest również macierz T16:

2. Obliczenia na wartościach liczbowych

• Równanie kinematyki odwrotnej:

T01^-1 * T06 = T16

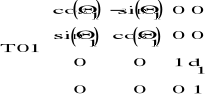
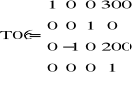
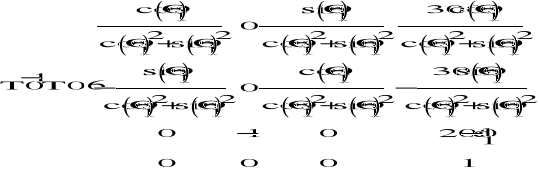
Po podstawieniu znanych wartości d₁=200 i uproszczeniach, macierz K przyjmuje następującą postać:

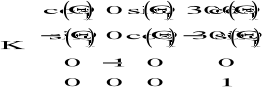
• Obliczenia Θ₁:

Porównanie współczynników z pozycji [2,3] macierzy K i macierzy T16

czyli arccos(1)= Θ₁

Otrzymujemy nieskończoną liczbę rozwiązań spowodowaną okresowością funkcji:

gdzie:

Po podstawieniu tych wartości do macierzy K otrzymujemy nową macierz.

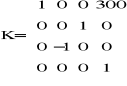
• Obliczenia Θ₂ i Θ₅:

• porównanie współczynników z pozycji [1,4] macierzy K i macierzy T16

czyli:

• porównanie współczynników z pozycji [2,4] macierzy K i macierzy T16

równanie sprowadza się do postaci :

0 = 0

• porównanie współczynników z pozycji [3,4] macierzy K i macierzy T16

czyli:

Uzyskujemy układ równań

Po podstawieniu znanych wartości a₃ = 150, a₆ = 50, d₄ = 100 przyjmuje taką postać:

Otrzymujemy nieskończony zbiór rozwiązań, spowodowany okresowością funkcji.

gdzie:

• Rozwiązaniami mieszczącymi się w przestrzeni roboczej manipulatora są:

K