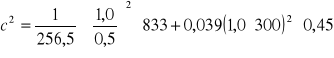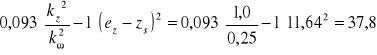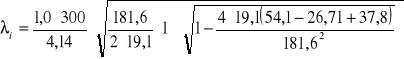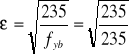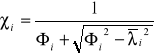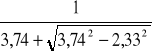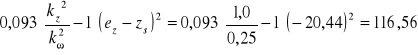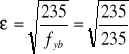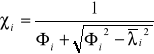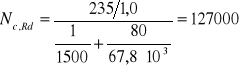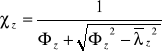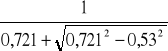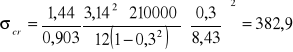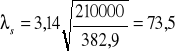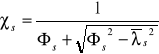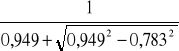Przykład 11-9. Wyznaczyć nośność wyboczeniową pręta ściskanego mimośrodowo o długości l = 3,0 m o przekroju pokazanym na rys. 11-9. Siła jest przyłożona w płaszczyźnie z-z na mimośrodach e_z = 8 cm, albo e_z = 8 cm. Maksymalny mimośród występuje na jednej z podpór, na drugiej zaś jest równy zeru przy podparciu końców pręta charakteryzującym się współczynnikiem długości wyboczeniowej
=
= 1,0,
= 0,5. Stal gatunku S235 o granicy plastyczności
MPa.

Jako wstępne przybliżenie można przyjąć, że nie występuje utrata stateczności miejscowej ścianek, gdyż przekrój jest bardzo niekorzystny ze względu na wyboczenie giętno-skrętne i wówczas siła krytyczna tej postaci wyboczenia jest mała, znacznie mniejsza niż to wynika z rozpatrzenia ściskania ze zginaniem.

Cechy charakterystyczne przekroju wynoszą: A = 15,0 cm², I_y = 563 cm⁴, I_z = 256,5 cm⁴,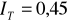
cm⁴,
= 833 cm⁶,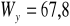
cm³, i_y = 6,08 cm, i_z = 4,14 cm_, ,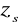
= 16,04 cm,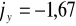
cm.

Rys. 11-9 Ceownik z usztywnieniami odgiętymi na zewnątrz

Wyboczenie giętno-skrętne:

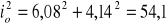
cm²,

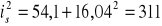
cm²,

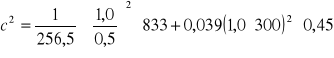
= 19,1 cm².

Obliczenie przy mimośrodzie e_y = + 8,0 cm:

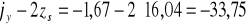
cm,

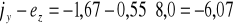
cm,

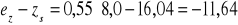
cm,

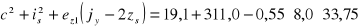
= 181,6 cm²,

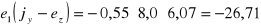
cm,

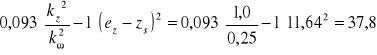
cm².

Smukłość zastępczą oblicza się ze wzoru (4-70):

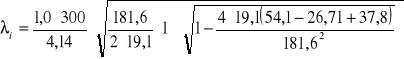
= 219,0,

Smukłość porównawcza

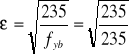
= 1,

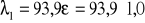
= 93,9.

Smukłość względna:

=
= 2,33, przy

Współczynnik wyboczeniowy (krzywa wyboczeniowa „c”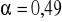
):

=
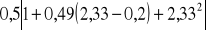
= 3,74,

=
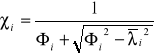
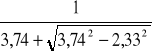
= 0,15.

Obliczenie przy mimośrodzie e_z = - 8,0 cm:

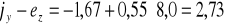
cm,

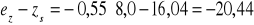
cm,

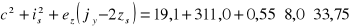
= 478,6 cm²,

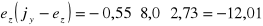
cm,

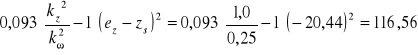
cm²,

= 360,3,

Smukłość porównawcza

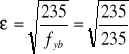
= 1,

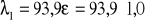
= 93,9.

Smukłość względna:

=
= 3,83 przy

Współczynnik wyboczeniowy (krzywa wyboczeniowa „c”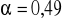
):

=
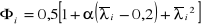
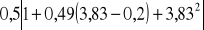
= 8,72,

=
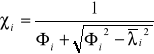
= 0,06.

Nośność pręta ze względu na wyboczenie giętno-skrętne:

• e_z = + 8,0 cm
  N = 52,9 kN,

• e_z = - 8,0 cm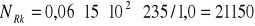
  N = 21,15 kN.

Nośność pręta ze względu na ściskanie ze zginaniem:

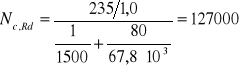
N = 127,0 kN > 52,9 kN > 21,15 kN.

Nośność pręta ze względu na ściskanie mimośrodowe z wyboczeniem giętym w płaszczyźnie z-z:

Długość wyboczeniowa wynosi:

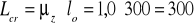
cm.

Smukłość giętna w rozpatrywanej płaszczyźnie wyboczenia

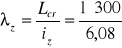
= 49,3.

Smukłość względna:

=
= 0,53 przy

Współczynnik wyboczeniowy (krzywa wyboczeniowa „c”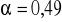
):

=
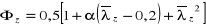
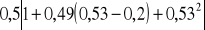
= 0,721,

=
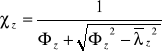
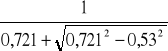
= 0,83.

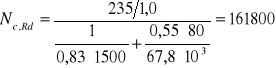
N = 161,8 kN > 52,9 kN > 21,5 kN.

Kształtownik kapeluszowy jest, jak wykazano obliczeniami niekorzystnym elementem ze względu na jego wyboczenie przestrzenne, zwłaszcza gdy siła podłużna jest przyłożona na mimośrodzie od strony stopek nieusztywnionych . Aby podwyższyć nośność pręta o takim przekroju, należy stopki nieusztywnione połączyć przewiązkami. Wówczas smukłość wyboczenia giętno-skrętnego, obliczona wzorami odnoszącymi się do profilu quasi-zamknięo-otwartego tylko nieznacznie różni się od smukłości wyboczenia giętnego w płaszczyźnie x-x, gdyż wynosi:

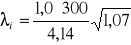
= 75.

Nośność pręta z przewiązkami wynosi:

=
= 0,80 przy

Współczynnik wyboczeniowy (krzywa wyboczeniowa „c”
):

=
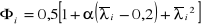
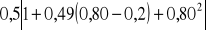
= 0,967,

=
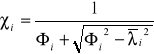
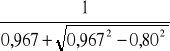
= 0,66.

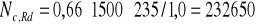
N = 232,7 kN > 52,9 kN > 21,5 kN.

Taki pręt należy jednak sprawdzić na możliwość dystorsyjnej utraty stateczności. Jako przybliżenie można zastosować rozwiązanie van der Maasa (por. [258] (4-82)).

,
.

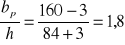
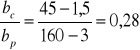
Z rys. 4-34 otrzymuje się
1,2, stąd K_s = 1,44.

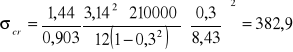
MPa,

, ,
,

=
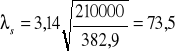
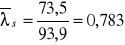
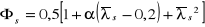
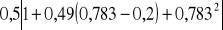
= 0,949,

=
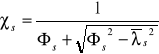
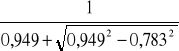
= 0,67.

Z porównań smukłości wynika, że w przypadku pręta z przewiązkami decydujący jest warunek nośności, wynikający z rozpatrzenia ściskania ze zginaniem. W takiej sytuacji należy jeszcze sprawdzić nośność według wzorów podanych w rozdz. 8, gdyż stopki nieusztywnione są wrażliwe na miejscową utratę stateczności.

285