Ćwiczenia 10 - 37 Przykład 34

Samochód o masie m porusza się po prostym odcinku drogi z prędkością V_p = 120km/h. W pewnym momencie rozpoczął hamowanie aż do zatrzymania się obliczyć czas drogi hamowania jeżeli wiadomo że współczynnik tarcia opon o drogę wynosi μ = 0.95. Opór tarcia toczenia i powietrza pominąć.

Rozwiązanie

y N

x

s mg

Rys. 34.1

Z warunku, że przyrost geometryczny pędu w pewnym przedziale czasu równa się popędowi sił działających w tym przedziale czasu

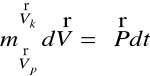
stąd

,
,
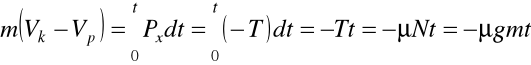
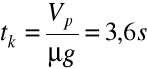
(a)

Równania różniczkowe ruchu samochodu

,
,
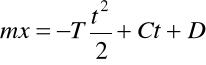
(b)

Warunki początkowe

Dla
,

Dla
,

Po podstawieniu C i D do (b) otrzymujemy

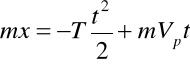
ponieważ
to równanie ruchu ma postać

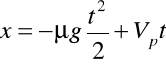
, gdy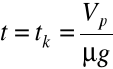
(patrz (a)) to
- 38 -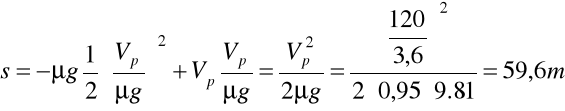
(34.1)

Przykład 35

Samochód o masie m porusza się po prostym odcinku drogi z prędkością V_p = 120km/h. W pewnym momencie rozpoczął hamowanie aż do zatrzymania się obliczyć czas drogi hamowania jeżeli wiadomo, że współczynnik tarcia opon o drogę wynosi μ = 0.95. Opór tarcia toczenia i powietrza pominąć.

Rozwiązanie

y N

x

s mg

Rys. 35.1

Przyrost energii kinetycznej punktu materialnego w skończonym przedziale czasu jest równy sumie prac, które wykonały w tym samym czasie wszystkie siły działające na ten punkt.

(35.1)

Praca
(a)

,
,
(b)

Podstawiając (b) do (a) otrzymujemy

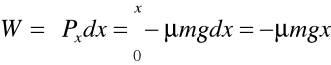
(c)

,
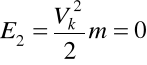
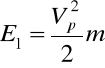
(d)

Wstawiając (c) i (d) do (35.1) i uwzględniając że x = s otrzymujemy

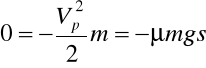
stąd

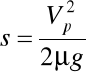
otrzymaliśmy wzór identyczny jak (34.1) - 39 -

patrz przykład 34. s = 59,6 m

Przykład 36

Obliczyć wartość liczbową krętu, względem początku układu współrzędnych xyz, punktu materialnego. Masa punktu m = 1.5 kg. Obliczenia przeprowadzić dla: x = 2 m, y = 1.5 m, z = 3.2 m,

V_x = 3 m/s, V_y = - 2 m/s, V_z = 1.5 m/s

Rozwiązanie

z

mV

m

r

k z

0 y

i x

y

x Rys. 36

Definicja wektora krętu K₀ względem początku układu 0

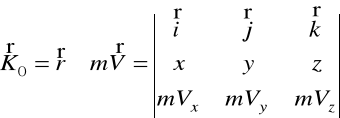
(36.1)

W naszym przypadku

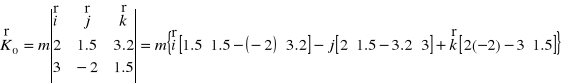
Przykład 37 - 40 -

Wyznaczyć z jaką najmniejszą prędkością V₁ należy wystrzelić pionowo w górę z powierzchni Ziemi pocisk, aby nie powrócił on z powrotem na Ziemię. Ziemię potraktować jako jednorodną kulę o promieniu R = 6370 km. Opór powietrza pominąć (rys. 37).

Ziemia

M P = mg V₁ P = mg_x V_x V x

m

R pocisk

x dx Rys. 37

x₁

Rozwiązanie

E₂ - E₁ = W (37.1)

;
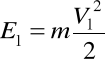
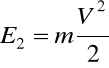
; (a)

(b)

Określenie siły P w funkcji x

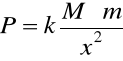
gdy x = R to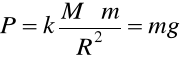
stąd

uwzględniając to otrzymujemy że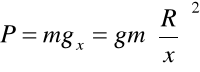

Podstawiamy P do (b)

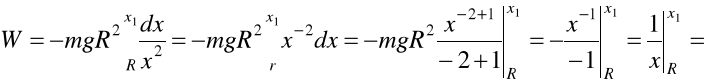
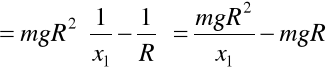
(c)

Wstawiamy (a) i (c) do (37.1)

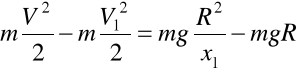
stąd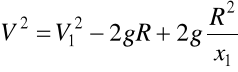
(d)

Z wzoru (d) wynika, że dla x₁ rosnącego V maleje bo 2gR²/x₁ maleje

Z wzoru (d) dla x₁ ∞,
czyli V = 0 dla

a więc dla

pocisk nie wróci na Ziemię.

Ćwiczenia 10

Przykład 38 - 41 -

Ciało o masie m ślizgające się z prędkością V₀ po idealnie gładkiej poziomej płaszczyźnie uderza w poziomą sprężynę, której drugi koniec jest unieruchomiony (rys. 38.1). Wyznaczyć prędkość ciała w funkcji ugięcia sprężyny, jeśli wiadomo, że stała sprężyny wynosi c (rys. 38.2) . Masę sprężyny pominąć. P

mg

P

V₀ x c = P/x

P

N x_sp x

x

Rys. 38.1 Rys. 38.2

Rozwiązanie

y mg

V P

x

T = 0

N

x₁ dx₁ Rys.38.3

x_k

Energia ciała o masie m w położeniach x₁ = 0 i x₁ = x

;

;
;

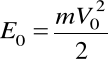
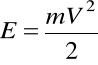
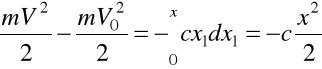
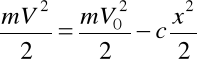
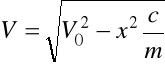
; jeśli V = 0 to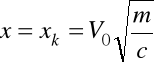

i od tego momentu ciało zaczyna poruszać się w przeciwnym kierunku.

V_k = 0

V_p = 120 km/h

V

V_p = 120 km/h

V

V_k = 0

T

T

j