SŁUP ZŁOŻONY Z ELEMENTÓW ŁĄCZONYCH NA GWOŹDZIE

Określić nośność pod obciążeniem średniotrwałym dwuteowego słupa złożonego o przekroju podanym na szkicu. Przyjąć wymiary przekroju oraz rozmieszczenie łączników wg przykładu belki złożonej. Wysokość słupa wynosi 4,725 m, podpory są przegubowe, brak stężeń pośrednich.

Dane:

Wysokość słupa L = 4,725 m

Klasa użytkowania 1

Gwoździe okrągłe, gładkie.

k_mod = 0,8 (EC5 - tabl.3.1)

1.Właściwości drewna (PN-EN 338:2009)

Klasa wytrzymałości C30

Wytrzymałość charakterystyczna na ściskanie f_c,0,k = 23 MPa = 2,3 kN/cm²

Wytrzymałość charakterystyczna na ściskanie

w poprzek włókien f_c,90,k = 2,7 MPa = 0,27kN/cm²

Średni moduł sprężystości wzdłuż włókien E_0,mean = 12 GPa = 1200 kN/cm²

5% kwantyl modułu sprężystości

wzdłuż włókien E_0,05 = 8,0 GPa = 800 kN/cm²

Gęstość charakterystyczna ρ_k = 380 kg/m³

Gęstość średnia ρ_m = 420 kg/m³

2. Dane geometryczne

Długość wyboczeniowa przy wyboczeniu względem osi y:

Długość wyboczeniowa przy wyboczeniu względem osi z:

Elementy przekroju poprzecznego słupa;

- pasy 2 x 4,5x160 (PN-75/D-96000)

- środnik 100x200 (PN-75/D-96000)

Gwoździe 4,5/100 są wbijane w dwóch szeregach co 60 mm.

3. Efektywne momenty bezwładności

3.1 Wyboczenie względem osi y.

K_ser = ρ_m^1,5d^0,81/30 = 420^1,5x4,5^0,8/30 = 822,5 N/mm = 8,225 kN/cm

Moduł podatności złączy w stanie granicznym nośności (SGN)

K_u = 2/3K_ser =2x8,225/3 = 5,483N/cm

Pole przekroju słupa:

A_tot = 2h_fb_f +h_wb_w = 2x4,5x16 + 20x10 = 144 +200 = 344 cm²

Moment statyczny pasa S_f:

z₁ = (h_f + h_w)/2 = (4,5 + 20)/2 = 12,25 cm

S_f,y = A_fxz₁ = 72x12,25 = 882,0 cm³

Współczynnik redukcyjny w stanie granicznym nośności:

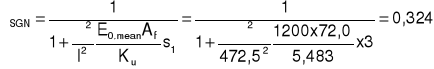
Efektywny moment bezwładności w stanie granicznym nośności:

Smukłość efektywna przy wyboczeniu względem osi y λ_ef,y:

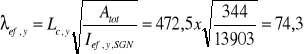
3.2 Wyboczenie względem osi z

Efektywny moment bezwładności w stanie granicznym nośności:

Smukłość efektywna przy wyboczeniu względem osi z λ_ef,z:

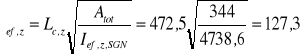
4. Nośność słupa N₁ ze względu na ściskanie

Wytrzymałość obliczeniowa na ściskanie:

Smukłość względna przy wyboczeniu względem osi z:

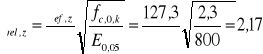
(EC5 - wz.6.22)

Współczynnik dotyczący prostoliniowości elementów dla drewna litego

β_c = 0,2 (EC5 -wz.6.29)

Współczynnik niestabilności

(EC5 - wz.6.28)

Współczynnik wyboczeniowy

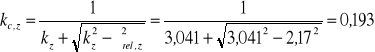
(EC5 - wz.6.26)

Nośność słupa ze względu na ściskanie:

5. Nośność słupa N₂ ze względu na łączniki

Łączniki pracują przy wyboczeniu względem osi y („podatnej”).

Przy pełnym wykorzystaniu nośności gwoździ:

, (EC5 - wz.C5)

gdzie:

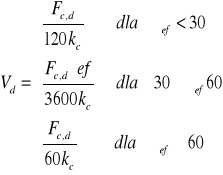
W tym przypadku:

> 60, oraz
zatem:

Należy wyznaczyć współczynnik wyboczeniowy k_c,y dla

Smukłość względna przy wyboczeniu względem osi y:

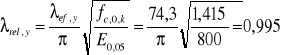
(EC5 - wz.6.22)

Współczynnik dotyczący prostoliniowości elementów dla drewna litego

β_c = 0,2 (EC5 -wz.6.29)

Współczynnik niestabilności

(EC5- wz.6.28)

Współczynnik wyboczeniowy

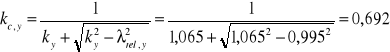
(EC5 - wz.6.26)

Z przekształcenia warunku nośności łączników:

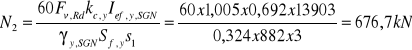
6. Nośność słupa N₃ ze względu na docisk do podwaliny

Nośność słupa N₃ należy wyznaczyć ze wzoru: (EC5-wz.6.4)

Efektywne pole docisku A_ef wynosi

• w przypadku słupów pośrednich (EC5 - 6.1.5(2))

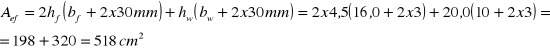
- w przypadku słupów skrajnych:

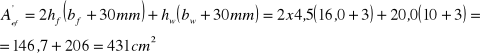
7. Nośność słupa

- pośredniego:

- skrajnego:

PRZEKRÓJ SKRZYNKOWY

Nośność słupa określić wyznaczając smukłości na podstawie efektywnych momentów bezwładności:

Współczynniki redukcyjne γ_y i γ_z wyznaczyć podstawiając do wzorów odpowiednio A_1,y i A_1,z.

z

y

b_f

16

10

b_w

h_f

h_w

4,5

4,5

20

z₁=12,25

h_f

A_1,y

A_1,z

b_w/2

b_w/2

z

y

b_f

y₁

h_f

h_w

z₁

h_f

---