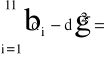Sprawozdanie z ćwiczenia nr A-27

Michał Tomaniak Marcin Kmiecik	Zespół nr 22
Wydział Elektryczny	Ocena z przygotowania:
Czwartek 1115 - 1400	Ocena ze sprawdzenia:
Data: 24 marzec, 1994	Zaliczenie:
Prowadzący:	Podpis:

Temat:Laminarny przepływ cieczy. Wyznaczanie współczynnika lepkości.

Podstawy teoretyczne.

Przy przepływach płynów tak jak przy ruchu ciał występuje siła oporu ruchu. Jeżeli do ciała będącego na powierzchni cieczy przyłożymy siłę równoległą do powierzchni cieczy, to ciało zacznie się poruszać ruchem jednostajnym. taki ruch powoduje siła lepkości F0.

Lepkością nazywamy nadanie warstwom cieczy, znajdującym się w różnej odległości od poruszającego się ciała, różnej prędkości.

Siła lepkości działająca na to ciało jest proporcjonalna do gradientu prędkości przesuwanych warstw cieczy i powierzchni ciała.

gdzie: - współczynnik lepkości

Siła lepkości powstaje na skutek przenoszenia x-owej składowej pędu przez cząstki szybsze na cząstki wolniejsze.

Ciecz idealna - jest to ciecz, w której ruch jednych warstw cieczy względem innych zachodzi bez tarcia tzn. poruszają się tylko te obszary cieczy, które zostały wprawione w ruch bezpośrednio przez siły zewnętrzne.

W cieczy idealnej obowiązuje zasada zachowania całkowitej energii mechanicznej.

Ciecz rzeczywista - jest to ciecz, w której ruch jednych warstw jest zależny od innych tzn. wprawienie w ruch pewnych obszarów cieczy pociąga za sobą ruch pozostałych obszarów.

Przepływ cieczy wokół dowolnego ciała zależy od gęstości , współczynnika lepkości , charakterystycznego wymiaru liniowego l oraz od prędkości przepływu. Dokładniej zależy on od bezwymiarowej kombinacji tych parametrów:

Powyższą wielkość nazywamy liczbą Reynoldsa. Dla różnych liczb Reynoldsa występuje inny przepływ cieczy tzn dla małych liczb Reynoldsa Re1 decydującą rolę w sile oporu odgrywa lepkość - wówczas przepływ cieczy nazywamy laminarnym - bezwirowym. Dla przepływu laminarnego formułuje się następujące prawo o podobieństwie przepływów :

Przepływy dwóch cieczy o różnych prędkościach, lepkościach i gęstościach są podobne jeżeli odpowiada im ta sama liczba Reynoldsa.

Dla przepływu laminarnego Stockes wyprowadził wzór na siłę oporu działającą na kulkę opadającą pod wpływem siły ciężkości w cieczy wypełniającej całą przestrzeń. Siłę oporu działającą na kulkę można opisać następująco:

gdzie: v - prędkość kulki, r - promień kulki, - współczynnik lepkości cieczy.

Dokładna analiza pokazuje, że kulka oprócz swojej masy posiada również masę dołączoną równą połowie masy cieczy wypartej przez kulkę. Ostatecznie prędkość kulki w danej chwili czasowej jest równa :

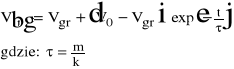
Obrazuje to poniższy wykres:

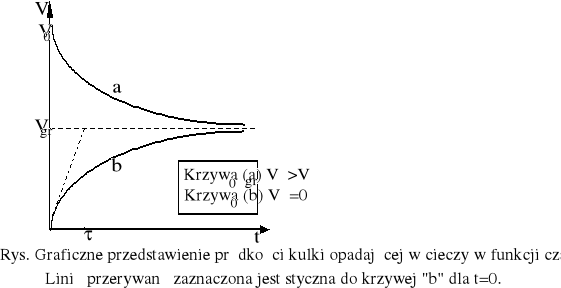
Z wykresu wynika, że po pewnym czasie ruch kulki można uznać za jednostajny i równy prędkości granicznej, określonej wzorem:

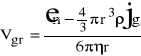
Wykonanie ćwiczenia.

1. Mierzymy na analitycznej wadze pewną liczbę kulek, a następnie wyznaczamy średnią masę jednej kulki. Z pomiarów otrzymaliśmy:

Masa 11 kulek - m=1998 mg

Średnia masa 1 kulki - m=181,2 mg

2. Za pomocą mikrometru mierzymy średnicę kulek.

3. Za pomocą suwmiarki mierzymy średnicę wewnętrzną rur:

- z gliceryną D=29,3 mm

- z olejem silnikowym D=29,9 mm

4. Do pionowo ustawionego cylindra z badaną cieczą wrzucamy kolejno 11 kulek, ustalając przy tym od którego miejsca ruch kulki można uznać za jednostajny. Następnie zaznaczamy ten odcinek i mierzymy jego długość.

5. Mierzymy stoperem czas opadania każdej z kulek ruchem jednostajnym.

6. Wyznaczamy średnią prędkość graniczną Vgr.

- dla oleju silnikowego

- dla gliceryny

7. Podstawiając otrzymane dane wyznaczamy lepkość cieczy:

Korzystamy przy tym ze wzoru:

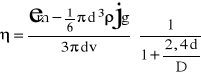
gdzie: m - masa kulki, d - średnica kulki, D - średnica cylindra z cieczą v - prędkość graniczna, g - przyśpieszenie ziemskie, - gęstość badanej cieczy

Po podstawieniu otrzymujemy:

- dla oleju silnikowego =0,24

- dla gliceryny =0,17

Rachunek błędów

1. Wyznaczamy błąd średnicy kulki. Ze względu na przewagę błędów przypadkowych nad systematycznymi błąd ten wyznaczamy za pomocą rozkładu Studenta.

Nr kulki	di	(di-d)		(di-d)2
i	[mm]	[mm]		[mm2]
1	3,39	-0,2882		0,0834
2	3,41	-0,3082		0,0949
3	3,42	-0,3182		0,1012
4	3,41	-0,3082		0,0949
5	3,28	-0,1782		0,0317
6	3,18	-0,2682		0,0061
7	3,37	-0,3882		0,0719
8	3,49	0,7419		0,1506
9	2,36	0,6618		0,5502
10	2,44	0,7319		0,4480
11	2,37	0,6512		0,5355
d= = 3,1018			2,1586

Podstawiając dane z powyższej tabeli wyliczamy

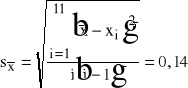
Znajdujemy wartość błędu dla poziomu ufności =0,997

Ostatecznie otrzymujemy, że :

d=0,25

czyli d=(3,100,25) 10-3 m

2. Wyznaczamy błąd prędkości v.

Korzystamy z metody różniczki zupełnej:

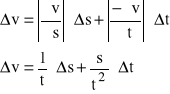
gdzie: s=10-3 m (dokładność odczytu drogi z podziałki milimetrowej)

t=0,6 s (dokładność odczytu czasu ze stopera)

Po podstawieniu otrzymujemy:

- dla oleju silnikowego v=0,03

czyli v=(18,53)10-2 m/s

- dla gliceryny v=0,06

czyli v=(26,16)10-2 m/s

3. Wyznaczamy błąd współczynnika lepkości

Korzystamy z metody różniczki zupełnej:

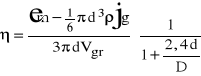
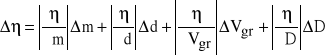
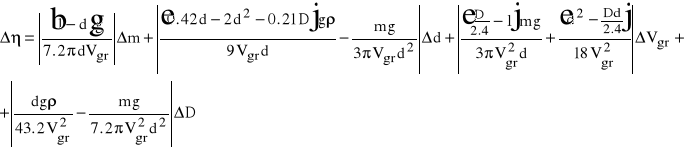
Po podstawieniu i obliczeniu otrzymujemy:

- dla oleju silnikowego

=0,114

czyli =(240114)10-3

- dla gliceryny

=0,082

czyli =(17082)0-3

3. Zestawiamy w tabeli oszacowane błędy pomiarów prostych.

Wielkość mierzona	Oznaczenie błędu	Oszacowanie błędu		Uzasadnienie
masa kulek	m	0,2 10-3 kg		Dokładność wagi analitycznej
droga przelotu	s	10-3 m		Dokładność skali (papier milimetrowy)
czas przelotu	t	0,6 s		2*czas reakcji+dokładność stopera
śred. cylindra	D	10-4 m		Dokładność suwmiarki

Laboratorium z Fizyki.

Strona nr 6

---