Badanie obwodów nieliniowych.
Celem ćwiczenia jest zapoznanie się z właściwościami elementów i obwodów nieliniowych prądu stałego.
1. Elementy nieliniowe i ich charakterystyki napięciowo-prądowe.
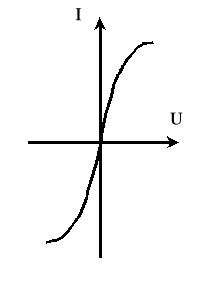
Elementami nieliniowymi nazywamy takie elementy, które nie spełniają zasady superpozycji. Obwód elektryczny, który zawiera element nieliniowy nazywamy obwodem nieliniowym. W przypadku obwodów prądu stałego mamy do czynienia z rezystancyjnymi elementami nieliniowymi. Charakterystyki napięciowo-prądowe tych elementów nie są liniami prostymi (rys. 1) i można je przedstawić w formie wykresu U=f(I) lub za pomocą wzoru matematycznego.
Rezystancyjnymi elementami nieliniowymi są np. diody, lampy neonowe, żarówki itp.
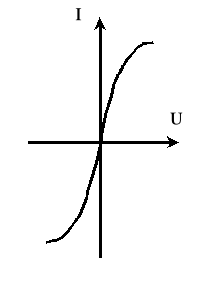
Rys..1.Przykłady charakterystyk napięciowo-prądowych elementów nieliniowych.
Wartość rezystancji elementu nieliniowego jest zmienna i zależy od punktu pracy (na charakterystyce U=f(I)). Dla zdefiniowania rezystancji elementu nieliniowego stosuje się dwa pojęcia:
rezystancja statyczna Rst,
rezystancja dynamiczna Rd.
Rezystancję statyczną elementu nieliniowego wyznacza stosunek napięcia na tym elemencie do prądu w nim płynącego:
![]()
(3.1)
Można ją również wyznaczyć graficznie (rys.2). Rezystancja statyczna jest proporcjonalna do tangensa kąta β utworzonego przez oś I oraz sieczną przeprowadzoną przez początek układu współrzędnych i dany punkt na charakterystyce.
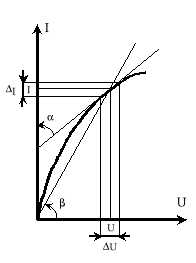
Rys.2. Metoda wyznaczania rezystancji statycznej i dynamicznej.
Rezystancję dynamiczną określa granica stosunku przyrostu napięcia, do przyrostu prądu:
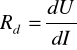
(2)
Ze wzoru tego można skorzystać wtedy, gdy dana jest zależność U=f(I), w postaci wzoru matematycznego.
Graficznie rezystancję dynamiczną można wyznaczyć korzystając ze wzoru:
![]()
Jak widać z rys. 2. rezystancja dynamiczna jest proporcjonalna do tangensa kąta α, który tworzy styczną, przeprowadzoną przez dany punkt na charakterystyce oraz oś I
2. Elementy nieliniowe połączone szeregowo, równolegle i szeregowo-równolegle.
Do wyznaczenia napięć, oraz rozpływu prądów w obwodzie nieliniowym niezbędna jest znajomość charakterystyk napięciowo-prądowych jego elementów.
W przypadku połączenia szeregowego elementów nieliniowych (rys.3), o charakterystykach napięciowo-prądowych UR1(I) oraz UR2(I) należy wykreślić charakterystykę UR2(I) elementu o R2.
Zgodnie z prawami Kirchhoffa przy połączeniu szeregowym przez rezystancję R1 i R2 płynie prąd o tej samej wartości powodując powstanie spadków napięć UR1 i UR2, czyli U=UR1+UR2. Powtarzając to sumowanie dla wielu wartości prądu, otrzymamy charakterystykę URZ(I), która pozwala na analizę rozpatrywanego obwodu. Przyłożenie napięcia U do obwodu (rys. 3b) spowoduje przepływ prądu I, a napięcia na poszczególnych elementach będą równe odpowiednio: UR1 oraz UR2.
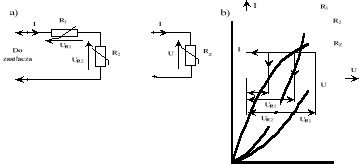
Rys. 3. Połączenie szeregowe elementów nieliniowych: a) schemat układu, b) charakterystyki.
Dla połączenia równoległego elementów nieliniowych (rys.4) charakterystykę elementu zastępczego można otrzymać przez zsumowanie prądów płynących przez poszczególne elementy, dla kilku wartości napięcia, np. przyłożenie napięcia U do obwodu spowoduje przepływ prądu o wartości I=I1+I2 (rys. 4b).
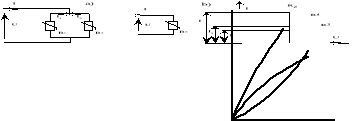
Rys 3.4. Połączenie równoległe elementów nieliniowych: a) schemat układu, b) charakterystyki.
Sposób posługiwania się charakterystykami U(I) elementów nieliniowych w obwodach złożonych wyjaśnia przykład analizy układu szeregowo-równoległego o danych charakterystykach napięciowo-prądowych poszczególnych elementów (rys. 5).
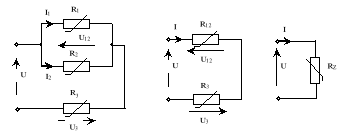
Rys.5. Schemat połączenia mieszanego elementów nieliniowych.
Dla analizy tego układu należy narysować wykresy U=f(I) wszystkich elementów w jednym układzie współrzędnych (rys.6), a następnie wyznaczyć charakterystyki elementów zastępczych.
Elementy R1 i R2 są połączone równolegle, czyli można je zastąpić elementem R12 o charakterystyce U12=f(I) otrzymanej przez zsumowanie prądów płynących przez te elementy dla danego napięcia. Otrzymano więc połączenie szeregowe elementów R12 oraz R3 o danych charakterystykach napięciowo-prądowych, które pozwalają wyznaczyć zależność U(I) nieliniowego elementu zastępczego RZ.
Jeżeli obwód pracuje przy wymuszeniu napięciowym U=U', to jak wynika z charakterystyki zastępczej (rys. 6) popłynie w nim prąd o wartości I'.
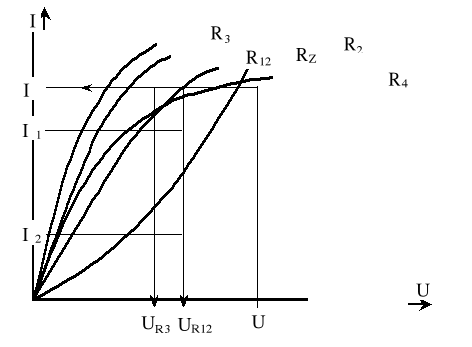
Rys. 6. Wyznaczanie charakterystyki zastępczej dla połączenia mieszanego elementów nieliniowych.
Przepływ prądu I' spowoduje powstanie spadków napięć U12 i U3 na elementach R12 oraz R3. Wartości tych napięć wyznaczają charakterystyki U12=f(I) oraz U3=f(I). Dla danego napięcia U12 z charakterystyk napięciowo-prądowych elementów R1 i R2 określić można prądy I1 i I2.
b)
a)
Wyszukiwarka