nr ćw. 108	data 20.01.1995	Jacek Zając	Wydział Elektryczny	Semestr III	grupa I1
prowadzący mgr. Ewa Mykowska					przygotowanie	wykonanie	ocena końcowa

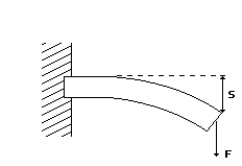
Temat: Wyznaczanie modułu Younga metodą ugięcia

Wiadomo że gdy na podłużny pręt działa siła prostopadle do jego długości, doznaje on ugięcia, a wielkość tzw. strzałki ugięcia S jest zawsze proporcjonalna do siły F, a także zależy od wymiarów geometrycznych pręta, sposobu jego mocowania i rodzaju materiału z którego jest on wykonany. Pręt na rysunku pod działaniem siły ugina się w ten sposób że górne warstwy pręta są rozciągane a dolne ściskane. W środku wysokości istnieje warstwa, której długość nie ulega zmianie. Przekroje prostopadłe pręta, przy braku obciążenia są wzajemnie równoległe, tworzą natomiast kąt
po przyłożeniu siły.

Na rysunku obok zaznaczyłem rozpatrywane przekroje przez 1 i 2 oraz kąt
między 1 i 2 (1' jest równoległym przesunięciem przekroju 1 do linii przecięcia warstwy neutralnej N z przekrojem 2).

Jeśli zacznę rozpatrywać element pręta o długości
, grubości
i szerokości b znajdujący się w odległości x od krawędzi zamocowanej i na wysokości y powyżej warstwy środkowej to na skutek ugięcia belki badana warstwa ulega ugięciu o
.

Zgodnie z prawem Hooke'a wydłużenie jest proporcjonalne do siły i długości początkowej oraz odwrotnie proporcjonalne do powierzchni przekroju

gdzie E - moduł Younga,
- siła rozciągająca badaną warstwę elementarną.

Taka sama siła, lecz przeciwnie skierowana, działa na warstwę elementarną położoną symetrycznie poniżej warstwy neutralnej N.

Moment siły
względem warstwy N wynosi

Całkowity moment M sił działających na wszystkie warstwy zawarte między przekrojami 1 i 2 obliczam całkując powyższe równanie względem y po całej grubości

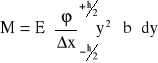
(1)

Jeśli oznaczę

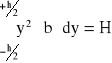
(2)

to równanie (1) mogę napisać w postaci

(3)

Równanie to otrzymałem rozpatrując odkształcenie pręta, którego bezpośrednią przyczyną jest siła F przyłożona do jego końca. Moment tej siły względem przekroju 2 wynosi
lub zaniedbując wielkość
jako małą w porównaniu z x

(4)

Kąt
jest zawarty między stycznymi do pręta w punktach, gdzie przekroje 1 i 2 przecinają górną powierzchnię. Na podstawie rysunku mogę napisać następujący związek

Wstawiając powyższe równanie do wzoru (3) i porównując wzory (3) i (4) otrzymuję elementarną strzałkę ugięcia

Całkowitą strzałkę ugięcia otrzymuję całkując powyższe równanie po całej długości pręta

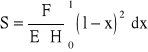
Po scałkowaniu, wyrażenie na całkowitą strzałkę ugięcia przyjmuje postać

Wartość współczynnika H zależy od kształtu i rozmiarów geometrycznych pręta. Gdy przekrój jest prostokątem o wysokości h i szerokości b, to całkowanie równania (2) prowadzi do wyniku

Całkowanie podobnego wyrażenia dla przekroju kołowego daje

Podstawiając wartości współczynników H otrzymuję odpowiednio dla obu przekrojów strzałki ugięcia

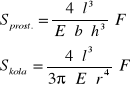
Otrzymane powyżej wzory odnoszą się do pręta jednostronnie obciążonego i jednym końcem umocowanego. Równania te mogę łatwo dostosować do sytuacji, gdy pręt jest swobodnie oparty dwoma końcami i obciążony w środku.

Zachowuje się on wtedy tak, jak gdyby był zamocowany w środku, a na jego końce działały siły
skierowane ku górze. Siła
działa wtedy na pręt o długości
.

Po uwzględnieniu tych warunków w poprzednich wzorach uzyskuję wzory na strzałki ugięcia prętów

dwustronnie podpartych

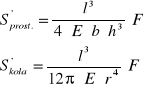
A z tych wzorów mogę już łatwo obliczyć moduł Younga. Po wykonaniu prostego przekształcenia mam moduł Younga dla przekroju prostokątnego

i dla przekroju kołowego

.

Przebieg doświadczenia

1. Zmierzyć wymiary poprzeczne pręta.

2. Zmierzyć odległości między krawędziami podpierającymi i wyznaczyć środek pręta.

3. Wypoziomować katetometr i przy jego pomocy wyznaczyć położenie górnej krawędzi pręta

nieobciążonego
.

4. Obciążając kolejno środek pręta ciężarkami (wg kolejności 1+2+3+4+5) odczytywać położenie

górnej krawędzi pręta.

5. Powtórzyć pomiary strzałki ugięcia przy zmniejszaniu obciążenia.

6. Obliczyć wartości średnie modułu Younga E i oszacować błędy
.

Pomiary zostały przeprowadzone dla czterech różnych prętów

Tabele wyników:

2.1. Masy obciążników:

Lp	m [kg]
1	0.2
2	0.2
3	0.5
4	0.5
5	0.5

2.2. Pręt o przekroju kwadratowym.

2.2.1.Wymiary: b = 8 mm,

a = 8 mm,

l = 60.5 mm,

h0 = 573.7 mm.

2.2.2. Tabela wynikw:

Lp	obciąźen. [g]	wysokość h [mm]	strzałka s [mm]	moduł Younga 1010 [N/m2]
1	200	573.34	0.36	7.3661861038
2	400	572.90	0.80	6.6295674951
3	900	572.03	1.67	7.1456416112
4	1400	571.10	2.60	7.1395342243
5	1900	571.08	2.62	9.6154032340
6	1700	570.60	3.10	7.2711385414
7	1200	571.63	2.07	7.6864550665
8	700	572.40	1.30	7.1395345543
9	200	573.34	0.36	7.3661861038
10	500	572.82	0.88	7.5335994278
11	1000	571.95	1.75	7.5766485624
Eśr.	7.4972631450 1010 N/m2
sn	0.722866846 1010
sn-1	0.758149144 1010

2.3. Pręt o przekroju kołowym.

2.3.1. Wymiary: r = 7 mm,

l = 60.5 mm,

h0 = 573.8 mm.

2.3.2. Tabela wynikw:

Lp	obciążen. [g]	wysokość h [mm]	strzałka s [mm]	moduł Younga 1010 [N/m2]
1	200	573.39	0.41	10,453798390
2	400	573.00	0.80	10,278930074
3	900	572.10	1.70	10,100094894
4	1400	571.50	2.30	9,934528958
5	1900	570.23	3.57	10,211190748
6	1700	571.15	2.65	10,435260098
7	1200	571.58	2.22	10,113566755
8	700	572.47	1.33	10,389087990
9	200	573.39	0.41	9,9786603001
10	500	572.78	1.02	10,100389770
11	1000	571.84	1.96	10,367868786
Eśr.	10,234567677 10 10 N/m2
sn	0.114733125 1010
sn-1	0.120333117 10 10

3.Rachunek błędów:

Błąd średnich modułu Younga został policzony za pomocą arkusza kalkulacyjnego excel 5.0 i umieszczony w powyższych tabelkach.

4. Wnioski.

Porwnując otrzymane wyniki oraz dane zawarte w tablicy w skrypcie Stanisława Szuby pt. ”Ćwiczenia laboratoryjne z fizyki” na stronie 201 możemy stwierdzić, że badane pręty wykonane były z miedzi (pręt o przekroju kwadratowym) i mosiądzu (pręt o przekroju kołowym). Niewielkie odchyłki od wartości nominalnych mogą być następstwem warunkw panujących w sali w czasie przebiegu ćwiczenia (np. temperatura panująca w sali znacznie odbiegała od 20C). Stosunkowo duża wartość odchylenia standardowego wynika z dużej rozbieżności wynikw, ktre są konsekwencją niedokładności odczytu i zamocowania prętw.