Parametry układu:

1Objętość właściwa-objętość zajmowana w dowolnych warunkach przez substancję o masie 1 kg, wyrażona w metrach sześciennych na kilogram. Jest odwrotnością gęstości.Objętość właściwa odnosi się zwykle do gazów i jest jedną z funkcji stanu. Znając jej wartość i wartość dowolnego innego parametru stanu, można wyznaczyć pozostałe funkcje i parametry stanu.

2Gęstość-masa jednostki objętości, dla substancji jednorodnych określana jako stosunek masy m do objętości V:
Gęstość jest cechą charakterystyczną substancji, a w określonych warunkach standardowych stanowi jedną z najważniejszych cech substancji - służy do obliczania masy i ciężaru określonej objętości substancji.

3Ciężar właściwy-γ, stosunek ciężaru ciała do jego objętości:
W odróżnieniu od gęstości, ciężar właściwy zależy też od siły ciążenia, czyli w warunkach nieważkości wynosi zero, gdy gęstość pozostaje taka sama (podobnie jak masa). γ stanowi ciężar odniesiony do jednostki objętości płynu:γ = ρ g. Jednostką ciężaru właściwego jest 1kg / (m² s² ), co wynika z poniższego zapisu:(kg/m³ )(m/s²) = (N m)(g m³ s²) = (N m s²)/(m m³ s²) = (N/m²)(1/m) = Pa/m

4Temperatura- jest miarą stanu cieplnego danego ciała. Temperaturę można ściśle zdefiniować tylko dla stanów równowagi termodynamicznej, z termodynamicznego bowiem punktu widzenia jest ona wielkością reprezentującą wspólną własność dwóch układów pozostających w równowadze ze sobą. Temperatura jest związana ze średnią energią kinetyczną ruchu i drgań wszystkich cząsteczek tworzących dany układ i jest miarą tej energii.

5Ciśnienie-to wielkość skalarna określona jako wartość siły działającej prostopadle do powierzchni podzielona przez powierzchnię na jaką ona działa, co przedstawia zależność:
W przypadku gazów w stanie ustalonym w spoczynku, ciśnienie jakie gaz wywiera na ścianki naczynia jest funkcją objętości, masy i temperatury i dlatego w termodynamice traktowane jest jako funkcja stanu.

6Strumień objętościowy-(objętościowe natężenie przepływu) - iloczyn prędkości (v) czynnika przepływającego przez przewód rurowy (rurę) i powierzchni przekroju S tego przewodu.Q = vS

7.Gaz doskonały definiować można zarówno na poziomie mikroskopowym (przez podanie właściwości elementów, z których jest zbudowany), jak i na poziomie makroskopowym (poprzez podanie jego właściwości jako całości). Równanie stanu - równanie Clapeyrona

 Pełna postać równania stanu gazu doskonałego jest następująca:p V = n R T i nazywane jest ono równaniem Clapeyrona. Przy czym p oznacza ciśnienie gazu, V - objetość, T - temperaturę, n - liczbę moli gazu a R jest tzw. stałą gazową równą R = 8, 314 J/mol·K.  Nic nie przeszkodzi, używając związku R = N_A k zapisać równania następująco:p V = N k T gdzie k = R / N_A jest stałą Boltzmanna.Na uwagę zasługuje fakt, że wymiarem prawej (i lewej) strony jest wymiar energii. 

8.Gaz pół doskonały-Gaz półdoskonały różni się tym od gazu doskonałego, że w jego drobinach występują drgania atomów. Gaz rzeczywisty zachowuje się jak gaz półdoskonały lub doskonały pod dostatecznie niskim ciśnienie.

9.Prawa do gazu doskonałego-1) Boylea Mariottea Jeżeli w =idem to p*V=idem 2)GayLussaca- Charlesa

Jeżeli p= idem to objętość właściwa to objętość właściwa V=V₀(1+T);V/T=idem V₀-obj.wł gazu w temp 0⁰C -termiczny wsp rozszerzalności objętości gazu odniesiony do obj V₀ jest ustalony eksperymentalnie  (1/273,15) *(1/K)Założymy że t=idem

p-stałe ciśnienie bezwzgl [N/m²] V- objętość właściwa [m³/kg] R-indywidualna stała gazowa [Nm/kgK]T-t emp benzyny 3)Awogadra liczba drobin zawartych w jednakowej objętości różnych gazów doskonałych w tych samych warunkach termicznych (temp i ciśnienie gazów jest takie same)

(MR) jedn indywidualnej stałej gazowej 8314 [J/kmolK]

R=(MR)/M

M₁*R₁= M₂*R₂₌ M*R

P*V=R*Tp(MV)=MR*T

P*V=m*R*Tp*V=n(MR)*T

MV;(MR)(B)nie zależy od rodzaju gazu

n,m- masy

10.Prawo Daltona-Prawo ciśnień cząstkowych zostało opublikowane przez Daltona w 1810 r. Głosi ono:"Ciśnienie wywierane przez mieszaninę gazów jest równe sumie ciśnień wywieranych przez składniki mieszaniny, gdyby każdy z nich był umieszczany osobno w tych samych warunkach objętości i temperatury, jest ono zatem sumą ciśnień cząstkowych." W formie matematycznej można je wyrazić jako:
p=p_ps+p_h ps-pow. Suchego h- porcjalne pary wodnej.

11.Ciepło właściwe- Całkowite ciepło przejęte przez ciało o masie m podczas podgrzewania od T₁ do T₂ jest równe ciepłu dostarczonemu z zewnątrz i ciepłu tarcia (ciepło wewnątrz ciał) Q_{c 1-2} =Q_1-2+Q_f przy czym
przekształcając wg.


Średnie ciepło właściwe
jest to ilość ciepła jaką należy dostarczyć jednej jednostce ilości substancji, aby zmienić temperaturę o 1K w całym rozpatrywanym okresie temp. Zależy od:rodzaju ciała ,temperatury t₁ t₂,warunków ogrzewania ciał. Stosunek C_p/C_v=χ Jeżeli mam ciało masie m i podgrzewam od t do Δt+t to nastąpi przyrost ciepła ΔQ_c

-rośnie wraz ze wzrostem t i jest wysokością prostokąta o szerokości (t₂-t₁). F pole figury nieregularnej równe polu prostokąta o wysokości. Wielkości ciepła właściwego C i szerokości t₂-t₁. Pole figury F=(t₂-t₁)*c

12..I zasada termodynamiki- W układzie odosobnionym tzn. osłoniętym osłoną adiabatyczną, ilość energii wewnętrznej układ jest stała E_d=ΔE_u+E_w [J] ⇒ równ bilansu energetycznego można traktować jako I zasadę termodynamiki dot. Układu zamkniętego. Energia doprowadzona do układu wyodrębnionego osłoną adiabatyczną pozostaje częściowo w układzie a część jest wyprowadzona z układu. Interpretacja graficzna - wykr. Sankeya

Jeżeli układ działa w sposób ustalony (jego energi nie zmienia się w czasie lub zmienia się w sposób periodyczny i po skończonej liczbie cykli wraca do wart. Początkowych) to bilans energetyczny przyjmuje postać
ponieważ
to do czynnego silnika
że jest rzeczą niemożliwą skonstruowanie perpetum mobile pierwszego rodzaju (silnika pracującego bez zasilania energią z zewnątrz).

Zmiana energii wewnętrznej układu zamkniętego jest równa energii, która przepływa przez jego granice na sposób ciepła lub pracy. ^[1]

dQ=dV+pdV dQ=dV+dL - 2 postacie

13.Pojęcie pracy bezwzględnej- Jest to praca wykonana przez czynnik termodynamiczny wtedy gdy ciśnienie otoczenia jest równe zero. Pracę tę można obliczyć rozpatrując układ cylinder - tłok

Przy ∞ małym dx czynnik wykonuje pracę dl=kdx, gdzie k - siła, dx droga. Przy pracy bez tarcia siłę k równoważy ciśnienie działające na tłok. Stąd: k=pA, gdzie p - ciśnienie, A- przekrój, dl=p A dx ⇒ dl=p dv, p - bezwzględne ciśnienie statyczne wewn. Cylindra, dv - przyrost objętości w cylindrze

14.Praca bezwzględna
; interpr. graficzna (założenie - znam zależność p od v)

L_1-2 - zależy od drogi przemiany a nie tylko od stanu początkowego i końcowego

L_1-2 - dotyczy przemian zachodzących bez strat na rzecz tarcia (wtedy dl <pdv)

Zastosowanie: w układach otwartych i zamkniętych, pseudoodwr. dl = p dv - dl_t = p dv - dQ_f stąd dl < p dv

dl_t - praca na rzecz tarcia, dQ_f - ciepło na rzecz tarcia

15.Praca techniczna-

Pracę fizyczną rozpatrujemy wg idealnej maszyny przepływowej tzn.

• nie występuje tarcie poruszających się względem siebie powierzchni

• zawory nie stawiają oporu

• w wewnętrznym zwrotnym położeniu tłok dotyka cylindra

Praca techniczna element. dL_t = -Vdp, L_t>0 gdy dp<0

Praca skończona L_{t 1-2} =

dL_t>0 gdy dp<0; dL_t<0 gdy dp>0

16.Przemiany termodynamiczne gazów doskonałych: Przemiany termodynamiczne

izobaryczna (p=const)

,

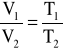
, L_t1,2 = 0, ,

izochoryczna (V=const)

,
,
,
,

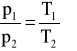
c) izotermiczna (T=const)

,
,
,

d) adiabatyczna (Q=const)

,

,

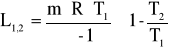
politropowa

,
,

,
,


,

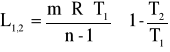
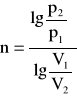
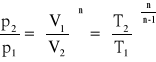
17.II zasada termodynamiki

Clausjusa ciepło nie może przejść samorzutnie od ciała o temp niższej do ciała o temp wyższej. Aby spowodować taki przepływ ciepła musimy zastosować lewo bieżną maszynę cieplną i wkładać do niej energię z zewnątrz, tzn. wywoływać zmiany w innych ciałach

Cornota-niemożliwy jest proces którego jedynym efektem jest zamiana ciepła pobranego ze żródła na równoważną mu prace.

ENTROPIA `S' Jest to funkcja stanu termodynamicznego, której zmiana równa się ilorazowi dostarczonego ciepłą i temperatury
; S - entropia całkowita

; s - entropia właściwa w odniesieniu do 1kg czynnika; dla źródła ΔS = -
źródło oddaje energię więc przyrost entropii jest ujemny. Entropia mówi nam o kierunku przemian zachodzących w przyrodzie.

Jeżeli układ jest jak na rys. i założenie: do tłok + cylinder możemy doprowadzić ciepło Q ze źródła ciepłą, przy czym Q = idem. Do cylindra mogę doprowadzić substancję o ilości dm i entropii właściwej s.

Wyróżniamy dwa przypadki:

I przemiana odwracalna

1. T_cz = T_źr ; b) brak tarcia dQ_t = 0

przyrost entropii układu odosobnionego Δs = π, natomiast elementarny przyrost ozn. dπ = ds._u+ds_ot

- przyrost entropii układu

- przyrost entropii otoczenia

Wniosek: W układzie odosobnionym sumą przyrostów entropii wszystkich ciał uczestniczących w zjawisku odwracalnym jest = 0. Warunek ten jest spełniony nawet w najmniejszej części zjawiska.

II przemiana nieodwracalna tzn. t_źr≠t_cz

18.Obieg termodynamiczny

Obieg prawobiezny- praca jest dodatnia czyli urządzenie wytwarza energię. Q_z=L_ob+Q_otocz. W cylindrze którego zawory są zamknięte trzyatomowy gaz doskonały podlega trzem przemianom. 1-2 adiabata, 2-3 izobara, 3-1 izochora.

Obieg lewobrzeżny-do urządzenie doprowadzana jest energia. Q_d+|L_ob|=Q_w E-wydajność urządzenia chłodniczego. E_ch=Q_d/|L_ob|

Obieg sprężarki chłodniczej gazowej `'parowej'', pompy ciepła

Obieg Carnota:

1-2 izotermiczna ekspansja następuje pobór ciepła

2-3 izentropowa ekspansja

3-4 kompresja izotermiczna następuje oddanie ciepła

4-1 kompresja izentropowa

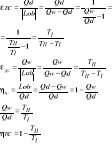
19.Zmiana stanu skupienia

Stopień suchości- jest to stosunek masy nasyconej suchej do pary mokrej.

Objętość właściwa pary mokrej- suma objętości cieczy w punkcie pęcherzyków i pary suchej nasyconej.

Entalpia właściwa-Dla entalpii właściwej można zapisać wzór definicyjny w następującej postaci:
gdzie:
— energia wewnętrzna właściwa
— objętość właściwa.

20.Powietrze wilgotne

Wilgotność bezwzględna-(gęstość wilgotności)- ro= m_w/V

Wilgotność względna- fi=m_w/m_wn w-pary wodnej wn-pary w. nasyconej

Wilgotność właściwa- x=m_pw/m_ps

Entalpia pary wilgotnej- jest równa sumie entalpi pow. Suchego i pary wodnej. i=(c_p+xc_pw)t+xr (c_p+xc_pw)=c

21.Elementy techniki cieplnej-

przewodzenie ciepła - przenoszenie ciepła w obrębie danego ciała od jednych drobin do drugich lub przez dyfuzję

konwekcja - (unoszenie ciepła) ciepło płynie z cząsteczkami płynu od ściany przegrody do rdzenia strumienia lub odwrotnie

promieniowanie - ciepło przenosi się od jednego ciała do drugiego w postaci energii promienistej (za pośrednictwem fal elektromagnet)

22.Prawo FOUTIERA-gęstość przewodzonego strumienia ciepła jest wprost proporcjonalna do gradientu temperatury
lub w postaci skalarnej

23.Prawo NEWTONA- Q =A-α(t_f - t_w)τ, gdzie t_w - temp pow ciała stałego, t_f - temp opływającego płynu, α - współczynnik, τ - czas, A - powierzchnia

α - ozn. ilość wymienionego podczas przejmowania przez jednostkę powierzchni w ciągu jednostki czasu.Przewodzenie - polega na przenoszeniu ciepła w obrębie danego ciała od jednych drobin do drugich, odbywa się tylko gdy drobiny ciała nie podlegają przesunięciom makroskopowym. Warunek spełniony podczas przepływu ciepła przez ciała stałe

24.Prawo PLANCA- prawo opisujące emisję światła przez ciało doskonale czarne znajdujące się w danej temperaturze.Zgodnie z nim emisja (i absorpcja) światła odbywa się w porcjach (kwantach) o energii hν, gdzie h - stała Plancka, ν - częstotliwość fali światła, a zależność zdolności emisyjnej ε od częstotliwości fali ν i temperatury T wyrażona jest wzorem (tzw. wzór Plancka):
gdzie c - prędkość światła, k - stała Boltzmanna.

E=(C₁lambda_t^-s)/(e^c_2/lambdatT-1)

25.Prawo STEFANO-BALTZMANA- opisuje całkowitą moc wypromieniowywaną przez ciało doskonale czarne w danej temperaturze. Zostało opracowane w 1879 przez Jožefa Stefana i Ludwiga Boltzmanna.
gdzie, Φ - strumień energii wypromieniowywany w kierunku prostopadłym do powierzchni ciała [W / m²] , σ - stała Stefana-Boltzmanna , T - temperatura w skali Kelvina E=C_o(T/100)

26.Prawo LAMBERTA- opisuje pochłaniane promieniowania elektromagnetycznego przy przechodzeniu przez częściowo absorbujący i rozpraszający ośrodek.Prawo może być matematycznie sformułowane na kilka sposobów: Absorpcja promienia światła przechodzącego przez kuwetę o na odcinku o długości l. E_fi=E_ocos(fi)

MECHANIKA PŁYNÓW

27.TEMPERATURA - jest miarą średniej energii kinetycznej atomów lub molekuł płynu. Do pomiaru temperatury można użyć przyrządu opartego na zależności temperatury od określonej właściwości płynu ( objętość , ciśnienie , przewodność cieplna i inne ).Podstawową jednostką temperatury bezwzględnej jest KELWIN [ K ].Dopuszcza się stopnie CELCJUSZA [⁰C ] przy czym: 0 ⁰C = 273,16 K (zero stopni Kelwina w skali Celsjusza wynosi -273,16 ⁰C).

28.CIŚNIENIE - stanowi sumaryczny efekt zderzeń molekuł z powierzchnią ściany lub powierzchnią zanurzonego ciała w płynie. W ujęciu fenomenologicznym, tzn. bazującym na molekularnej strukturze płynów, ciśnienie p, mierzone w [Pa ] wynosi p = F / A , F - parcie, [N], A - powierzchnia działania parcia, [m²]

Jednostką ciśnienia w układzie jednostek SI jest PASKAL [Pa]

29.GĘSTOŚĆ - przez gęstość ρ rozumiemy masę płynu odniesioną do jednostki objętości stąd:ρ = lim (Δm/ΔV) = dm/dV. Dla płynu w równowadze termodynamicznej gęstość wyraża zależność:ρ = m / VJednostką gęstości w układzie SI jest 1 kg/m³.

30.LEPKOŚĆ - czyli TARCIE WEWNĘTRZNE jest to zdolność płynu do przenoszenia naprężeń stycznych między sąsiednimi warstwami płynu, poruszającymi się z różnymi prędkościami względem siebie. Naprężenia styczne w płynie powstają także między płynem a ciałem stałym, np. ścianką zbiornika lub przewodu. Naprężenia stycznie nie występują w stanie spoczynku płynu. Miarą lepkości jest - DYNAMICZNY WSPÓŁCZYNNIK LEPKOŚCI - μ (mi)

31.RÓWANIE RÓWNOWAGI STATYCZNEJ:

Równowaga dotyczy równoważenia się sił masowych i sił powierzchniowych, co zapisuje się w postaci:

Fxdx+Fydy+Fzdz=dp/ro

,gdzie

i, j, k - wektory jednostkowe osi współrzędnych (wersory),

∂p/∂x, ∂p/∂y, ∂p/∂z - pochodne cząstkowe.

ρF_m = gradp = 0

Jest to wektorowy zapis równania równowagi płynu w postaci różniczkowej.

W układzie współrzędnych kartezjańskich równanie (6) można zapisać w postaci trzech równań

skalarnych, a mianowicie

w których X, Y, Z stanowią składowe jednostkowej siły masowej F_m w kierunkach trzech osi współrzędnych x, y, z. Mnożąc stronami równania (7) odpowiednio przez dx, dy, dz otrzymuje się:

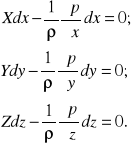
Z kolei, sumując te równania stronami, dostaje się; ρ( Xdx + Ydy + Zdz ) = (∂p/∂x)dx + (∂p/∂y)dy + ∂p/∂z)dz .Prawa strona zależności (9) jest różniczką zupełną dp, co można zapisać to krócej:

32.Napór na powierzchnie płaskie siła nacisku jaką płyn wywiera na daną powierzchnię. Siła ta jest normalna do danej powierzchni.Parcie jest związane z ciśnieniem wzorem
gdzie:
- wektor powierzchni nieskończenie małego fragmentu ds powierzchni S, p - ciśnienie hydrostatyczne panujące na poziomie, na którym znajduje się powierzchnia ds. Dla powierzchni płaskich i stałego ciśnienia w każdym punkcie powierzchni, wzór na parcie upraszcza się do postaci
Płyn w stanie spoczynku wywiera napór hydrostatyczny zarówno na dno jak i ścianę naczynia.Parcie na ścianę poziomą można zapisać

33.Wypór hydrostatyczny- siła stanowiąca wypadkową naporów hydrostatycznych działających na ciało częściowo lub całkowicie zanurzone w cieczy. Wypór skierowany jest przeciwnie do siły ciężkości, a jego wartość określa prawo Archimedesa. Zaczepiony jest umownie w tzw. środku wyporu, który pokrywa się ze środkiem masy wypartej cieczy. W przypadku statku lub jachtu wypór w warunkach statycznych równa się wyporności.

34.Równowaga wzgledna cieczy Równowaga względna. Jeżeli punkt materialny jest w równowadze (czyli spoczynku) względem układu ruchomego, to przyśpieszenie względne jest pw=0, a prędkość względna t>(O=0.Wynika stąd, że również przyśpieszenie Coriolisa jest pc=0, a zatem i siła Coriolisa Pc=0. Z równania (II), str. 137, otrzymamy więc (I) Pb + Pu=0. A więc: gdy punkt jest w równowadze względnej, silą bezwzględna równoważy się z silą unoszenia. Równowaga względna cieczy jest w przypadku, gdy ciecz jest spoczynku względem własnych cząstek.

35.Pochodna substancjonalna Ta pochodna dH/dt nosi nazwę pochodnej substancjonalnej dowolnej wielkości fizycznej. Pochodna ta jest sumą pochodnej lokalnej ∂H/∂t i pochodnej konwekcyjnej (v⋅∇)H. Pochodna ∂H/∂t oznacza zmianę wielkości H w czasie POCHODNA SUBSTANCJALNA Niech będzie rozważana wielkość fizyczna H, tzn. taka że: H = f ( x, y, z, t ). V=(V_x, V_y, V_z) Różniczkując cząstkowo tę zależność, otrzymuje się: dH = (∂H/∂t)dt + (∂H/∂x)dx + (∂H/∂y)dy + (∂H/∂z)dz Dzieląc stronami przez dt, dostaje się:

dH/dt = ∂H/∂t + (∂H/∂x)(dx/dt) + (∂H/∂y)(dy/dt) + (∂H/∂z)(dz/dt)

Zauważmy, że dx/dt = v_x; dy/dt = v_y; dz/dt = v_z, tj. są to odpowiednie składowe prędkości v w kierunku osi współrzędnych x, y, z.

Wobec tego zapis wyrażenia (5) upraszcza się do postaci: dH/dt = ∂H/∂t + (∂H/∂x)v_x + (∂H/∂y)v_y + (∂H/∂z)v_z

∂H/∂t - pochodna lokalna

(∂H/∂x)v_x + (∂H/∂y)v_y + (∂H/∂z)v_z - pochodna konwekcyjna

Pochodna ∂H/∂t oznacza zmianę wielkości H w czasie.

-przyśpieszenia lokalne

- przyspieszenia unoszenia

36.POLEM FIZYCZNYM nazywamy obszar, w którym każdemu punktowi w każdej chwili czasu jest jednoznacznie przyporządkowana określona wartość wielkości fizycznej (parametru) płynu. Mogą być różne pola fizyczne, jak pole ciśnienia, temperatury, prędkości i inne. Zespół pól określa przepływ płynu, stąd wynika klasyfikacja przepływów:

• pole ustalone, jeśli wielkość fizyczna nie zależy od czasu: ∂H/∂t = 0

H = f (x, y, z );

• pole nieustalone, jeśli wielkość fizyczna zależy od czasu: ∂H/∂t ≠ 0 i wobec tego H = f ( x, y, z, t );

• pole jednorodne i niejednorodne, gdy wielkość fizyczna jest stała lub niestała;

• pole ciągłe i nieciągłe;

• pole źródłowe i nieźródłowe;

• pole wirowe i bezwirowe (potencjalne ): wirowe - u ≠ 0; ω ≠ 0;

bezwirowe - u ≠ 0; ω = 0 (ω - prędkość kątowa);

• pole skalarne, wektorowe, tensorowe; jeśli wielkość fizyczna jest skalarem lub wektorem, lub tensorem;

• pole jedno-, dwu- i trójwymiarowe (liniowe, płaskie, płaskie osiowo-symetryczne i przestrzenne).

37.Równanie ciągłości:

Dla osi x:

Dla osi y:

Dla osi z:

R+A=0

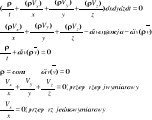
38. Równanie Eulera, równanie ruchu Eulera, siły działające w płyn

Siły powierzchniowe i siły masowe

39.Równanie bernulliego

Założenia

-ciecz jest nieściśliwa

- ciecz nie jest lepka

- przepływ jest stacjonarny i bezwymiarowy

Wyprowadzenie wzoru bernulliego

- przepływ jednowymiarowy, przepływ bezwirowy

równanie Eulera dla przepływu jednowymiarowego

1. przepływ ustalony

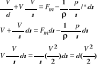
2. siły masowe są potencjalne
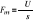
   U-potencjał

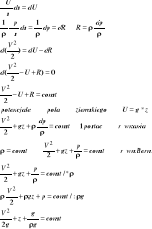
Dynamika płynów rzeczywistych

40.równanie mogera - poiseulle'a - przepływ laminarny w przewodzie kołowym

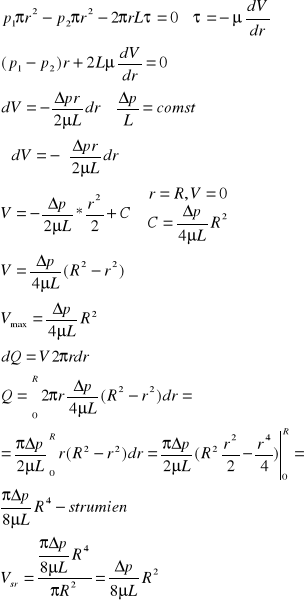
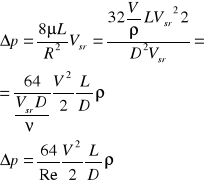
Prawo Hagena-Poiseuille'a

gdzie poszczególne symbole oznaczają:

Φ_V - strumień objętości przepływu,

V, dV/dt - objętość, pochodna objętości względem czasu,

z - współrzędna walcowa, długość liczona wzdłuż osi przewodu,

v_s - średnia prędkość płynu w kierunku z,

r - promień wewnętrzny przewodu,

η - współczynnik lepkości dynamicznej płynu,

p - ciśnienie uśrednione w przekroju przewodu,

-dp/dz - gradient ciśnienia wzdłuż osi z,

Δp - różnica ciśnień na końcach przewodu,

l - długość przewodu.

41.Ruch laminarny i turbulentny

Ruch laminarny (warstwy się nie nakładają) tory cząstek mało różnią się od siebie. Pozostające w ruchu medium można traktować jako zbiór oddzielnych warstw, poruszających się względem siebie z różną prędkością i nie mieszających się ze sobą. Ruch taki występuje w mediach o dużej lepkości (μ), np. lawa wulkaniczna. Re<2300

Ruch turbulentny ( warstwy mieszają się ze sobą) ruch cząstek płynu powoduje mieszanie się ze sobą rożnych warstw, Ruch ten występuje w mediach o względnie malej lepkości (μ), np. woda, powietrze. Re>50000

42.Równanie Darcyego-Weisbacha-równanie opisujące spadek ciśnienia płynu na skutek oporów jego przepływu w przewodzie.

λ - współczynnik oporu - f(Re)

l- długość przewodu^[1]

D - średnica (ew. zastępcza) przewodu

v - prędkość płynu

ρ - gęstość płynu

43.opory przepływu, opór tarcia i miejscowy (od czego zależą od Re i chropowatości - współczynnik oporu λ(Re, ε)

- poszukujemy funkcję zależną od zjawisk fizycznych

n=6, i=3 => n-i=3 poszukujemy funkcji o 3 wielkościach f(π₁, π₂, π₃)=0

-poszukujemy funkcji o wielkościach (ρ, V, D)

ρ^a1 V^a2 D^a3=1

- parametry bezwymiarowe z pozostałych wielkości

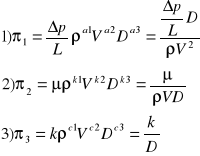
- poszukujemy funkcji

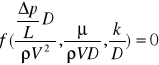
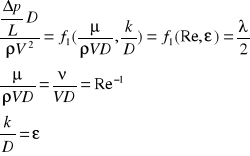
44 uogólnione prawo Bernoulliego + ze stratami

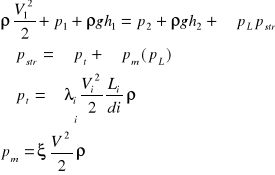
- współczynnik ξ możemy obliczyć dla nagłego rozszerzenia przewodu

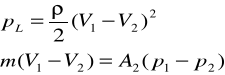
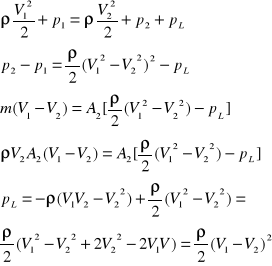
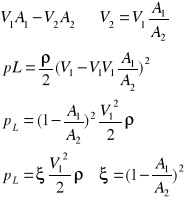
45. przepływy w kanałach otwartych, równanie jednostronne, prędkość, przekrój optymalny, wzór chezy'ego

- wzór chezy'ego

- przekrój optymalny- max strumień objętości przepływający kanałem o stałym nachyleniu i stałym przekroju poprzecznym- kształt okrągły będzie najbardziej optymalny

46.Porowatość ośrodka w ogólności

Porowatość powierzchniowa

Przepływ w ośrodku porowatym (prawo Darcyego)

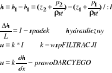
Dopływ do rowu

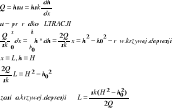
Dopływ do studni

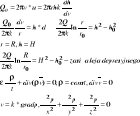
47.Opadanie swobodne cząstek

Siła oporu profilowanego - występuje zawsze gdy V>0

Rotametr - przyrząd do pomiaru strumienia objętości

1.Objętość właściwa

2.Gęstość

3.Ciężar właściwy

4.Temperatura

5.Ciśnienie

6.Strumień objętościowy

7.Gaz doskonały

8.Gaz pół doskonały

9.Prawa do gazu doskonałego

10.Prawo Daltona

11.Ciepło właściwe

12. I zasada termodynamiki

13.Praca bezwzględna

15.Praca techniczna

16.Przemiany termodynamiczne

17.II zasada termodynamiki

18.Obiegi termodynamiczne

19.Zmiany stanu skupienia

20.Powietrze wilgotne

21.Elementy techniki cieplnej

22.Prawo Fouriera

23.Prawo Newtona

24.Prawo Planca

25.Prawo Stefano-Baltzmana

26.Prawo Lamberta

27.Temperatura

28.Ciśnienie

29.Gęstość

30.Lepkość

31.Równanie równowagi statycznej

32.Napór na powierzchnie płaskie

33.Wypór hydrauliczny

34.Równowaga względna cieczy.

35.Pochodna substancjonalna

36.POLEM FIZYCZNYM

37.Równanie ciągłości:

38. Równanie Eulera

39.Równanie bernulliego

40.równanie mogera - poiseulle'a

41.Ruch laminarny i turbulentny

42.Równanie Darcyego-Weisbacha

43.opory przepływu, opór tarcia i miejscowy

44 uogólnione prawo Bernoulliego + ze stratami

45. przepływy w kanałach otwartych

46.Porowatość

47.Opadanie swobodne cząstek

dx - odległość przesunięcia tłoka

Jeżeli:

dv>0 to dl>0

dv<0 to dl<0

L_t=L_n+L_1-2+L_w+L_1-2+p₁v₁-p₂v₂

L_n - praca napełniania

L_1-2 - praca przemiany zamknietej

L_w - praca wytłaczania

zał. p₁>p₂

1. w.z.p. - przemiana napełniania

2. z.z.p. - ilość czynnika = const

ρ( Xdx + Ydy + Zdz) = dp

---