DEFINICJA SZEREGU CZASOWEGO

Definicja:

Szeregiem czasowym nazywamy zbiór wartości cechy w uporządkowanych chronologicznie różnych momentach (przedziałach) czasu.

Oznaczając przez
momenty (przedziały) czasu, w których obserwowano wartości pewnej zmiennej, a przez
wyniki obserwacji, szereg czasowy zapisujemy jako zbiór
1}

Produkcja energii elektrycznej w Polsce w latach 1991-1994

(dane miesięczne w mld kWh)

Miesiące	I	II	III	IV	V	VI	VII	VIII	IX	X	XI	XII
Lata
1991	14,0	12,9	12,8	11,3	10,6	9,2	9,0	9,0	9,3	11,2	12,1	13,3
1992	13,4	12,2	12,5	11,0	9,6	9,0	9,0	9,0	9,7	12,0	12,3	13,2
1993	13,4	12,2	12,8	10,7	9,3	8,9	8,7	9,1	9,8	11,5	13,0	13,5
1994	12,9	12,3	12,7	10,9	9,9	9,4	9,3	9,5	9,8	12,3	12,3	13,6

t	0	1	2	3	4	5	...	44	45	46	47
yt	14,0	12,9	12,8	11,3	10,6	9,2	...	9,8	12,3	12,3	13,6

PREZENTACJA GRAFICZNA SZEREGU CZASOWEGO

Elementy szeregu czasowego są reprezentowane przez punkty płaszczyzny o współrzędnych
, które łączy się z reguły odcinkami linii prostej.

Szereg czasowy produkcji energii elektrycznej

SKŁADNIKI SZEREGU CZASOWEGO

tendencja rozwojowa (trend) - ogólny kierunek zmian zjawiska w czasie będący wynikiem systematycznych, jednokierunkowych zmian (spadek lub wzrost) poziomu badanego zjawiska

wahania okresowe - rytmiczne wahania poziomu badanego zjawiska o określonym cyklu (okresie przebiegu)

wahania koniunkturalne - systemowe wahania poziomu badanego zjawiska obserwowane w dłuższych od roku okresach

wahania przypadkowe - nieregularne, nieprzewidywalne zarówno co do kierunku jak i siły zmiany poziomu badanego zjawiska

WYODRĘBNIANIE SKŁADNIKÓW SZEREGU CZASOWEGO

A. TREND

A.1. METODY WYRÓWNYWANIA MECHANICZNEGO - ŚREDNIE RUCHOME

średnie ruchome zwykłe - oblicza się z nieparzystej liczby sąsiadujących ze sobą wyrazów szeregu, tak aby uzyskany wynik móc przyporządkować całkowitej wartości t znajdującej się w środku uwzględnionego w obliczeniach przedziału czasowego:

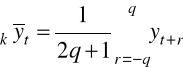
gdzie:

- liczba wyrazów szeregu uwzględnianych przy obliczaniu średniej ruchomej, przy czym q jest ustalony liczbą naturalną

Przykład:

(średnia trzyokresowa)

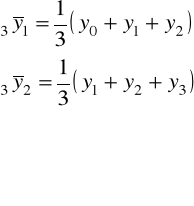
średnie ruchome scentrowane - oblicza się z parzystej liczby sąsiadujących ze sobą wyrazów szeregu, uwzględniając połowę wartości pierwszego wyrazu z danego cyklu wahań, następnie wszystkie pozostałe wyrazy składające się na pełny cykl wahań oraz połowy wartości pierwszego wyrazu z następnego cyklu wahań:

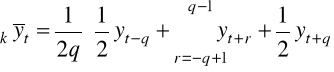
gdzie:

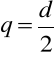
, przy czym d jest liczbą podokresów w cyklu wahań

Przykład:

(średnia przy czterookresowym cyklu wahań)

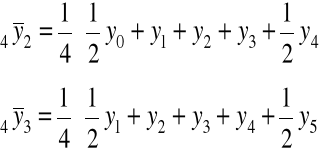
A.2. METODY ANALITYCZNE - MNK

Zakładając, że do opisu tendencji rozwojowej (trendu) stosujemy funkcję liniową
dobieramy tak wartości współczynników równania linii prostej, aby jej wykres możliwie dobrze "pasował" do punktów reprezentujących na wykresie poszczególne obserwacje z próby:

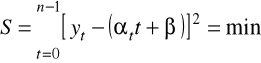
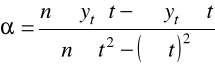
Lata i pory roku
1993 zima wiosna lato jesień	0 1 2 3	53 41 24 57	45,80 50,38	0,524 1,131	44,5 39,8 35,8 51,4
1994 zima wiosna lato jesień	4 5 6 7	70 60 41 77	54,88 59,50 63,38 66,00	1,276 1,008 0,647 1,167	58,8 58,3 61,2 69,4
1995 zima wiosna lato jesień	8 9 10 11	81 70 50 87	68,38 70,75 73,63 77,25	1,185 0,989 0,679 1,126	68,1 68,0 74,6 79,1
1996 zima wiosna lato jesień	12 13 14 15	94 86 64 99	81,00 84,25 87,63 91,38	1,160 1,021 0,730 1,083	79,0 83,5 95,5 90,0
1997 zima wiosna lato jesień	16 17 18 19	109 101 77 110	94,88 97,88 101,00 105,13	1,149 1,032 0,762 1,046	91,6 98,1 114,9 100,0
1998 zima wiosna lato jesień	20 21 22 23	123 120 95 126	109,75 114,00	1,121 1,053	103,4 116,4 141,8 113,5
	276	1915

Lata i pory roku
1993 zima wiosna lato jesień	0 1 2 3	53 41 24 57	0 41 48 171	0 1 4 9	45,80 50,38	41,097 44,461 47,826 51,191
1994 zima wiosna lato jesień	4 5 6 7	70 60 41 77	280 300 246 539	16 25 36 49	54,88 59,50 63,38 66,00	54,556 57,920 61,285 64,650
1995 zima wiosna lato jesień	8 9 10 11	81 70 50 87	648 630 500 957	64 81 100 121	68,38 70,75 73,63 77,25	68,015 71,380 74,744 78,109
1996 zima wiosna lato jesień	12 13 14 15	94 86 64 99	1128 1118 896 1485	144 169 196 225	81,00 84,25 87,63 91,38	81,474 84,839 88,204 91,568
1997 zima wiosna lato jesień	16 17 18 19	109 101 77 110	1744 1717 1386 2090	256 289 324 361	94,88 97,88 101,00 105,13	94,933 98,298 101,663 105,027
1998 zima wiosna lato jesień	20 21 22 23	123 120 95 126	2460 2520 2090 2898	400 441 484 529	109,75 114,00	108,392 111,757 115,122 118,487
	276	1915	25892	4324		1915,006

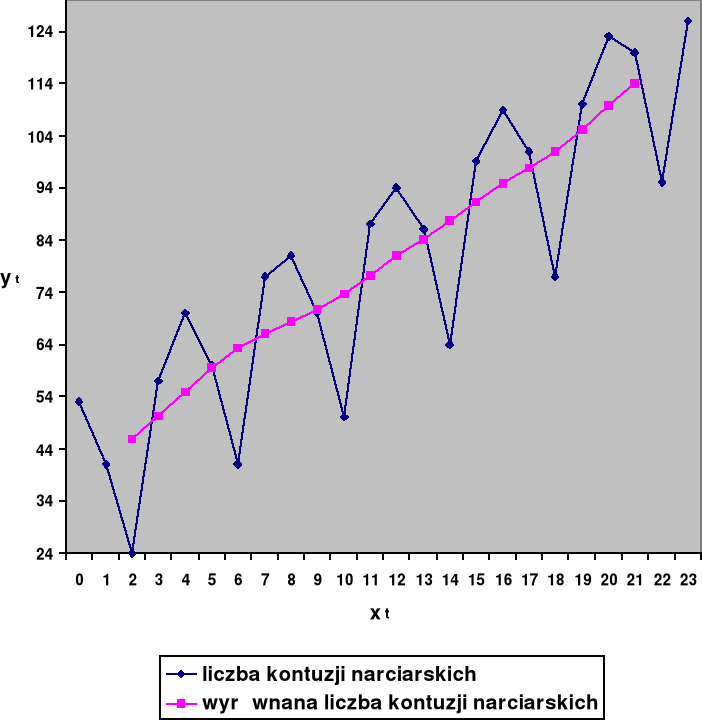
Przykład:

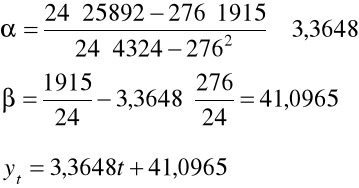
ANALIZA WAHAŃ OKRESOWYCH

1. WSKAŹNIKI WAHAŃ OKRESOWYCH DLA SZEREGU CZASOWEGO BEZ TRENDU

1⁰ Wprowadzamy oznaczenia:

• oznaczamy n-elementowy szereg czasowy z wahaniami okresowymi przez
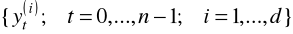
  , gdzie:

t - bieżący numer obserwacji,

i - numer podokresu w cyklu.

• oznaczamy zbiór numerów obserwacji, które dotyczą i-tego podokresu cyklu, przez:

• oznaczamy przez n_i liczebność zbioru N_i

2⁰ obliczamy średnią wartość badanej zmiennej w i-tym podokresie cyklu:

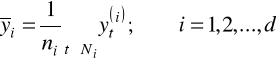
30 Obliczamy średnią z całego szeregu czasowego:

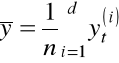
40 Obliczamy wartość wskaźnika wahań okresowych:

Wartość wyrażenia
mówi, o ile procent wartości zjawiska obserwowane w i-tym podokresie cyklu są, na skutek wahań okresowych, przeciętnie wyższe (znak +) lub niższe (znak -) od średniego zjawiska określonego przez trend.

5⁰ Wartość wskaźnika wahań okresowych nakładających się na trend w sposób addytywny:

2. WSKAŹNIKI WAHAŃ OKRESOWYCH DLA SZEREGU CZASOWEGO Z TRENDEM

B.1. WAHANIA OKRESOWE MULTIPLIKATYWNE

gdzie:

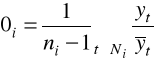
- surowy wskaźnik wahań okresowych,

przy czym:

- średnie ruchome (scentrowane)

N_i - zbiór numerów obserwacji, które dotyczą i-tego podokresu cyklu

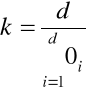
- wskaźnik korygujący

i jednocześnie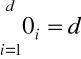

B.2. WAHANIA OKRESOWE ADDYTYWNE

1⁰ Wahania okresowe w jednostkach absolutnych

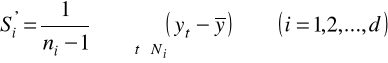
2⁰ Skorygowane wahania okresowe (suma odchyleń okresowych w obrębie cyklu wahań równa zeru)

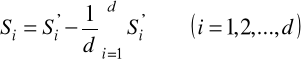
A.B. ELIMINACJA WAHAŃ SEZONOWYCH Z SZEREGU CZASOWEGO

1⁰ Wahania okresowe multiplikatywne

2⁰ Wahania okresowe addytywne

Przykład:

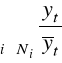
zima 5,891

wiosna 5,103

lato 3,342

jesień 5,553

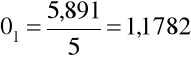
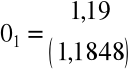
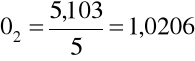
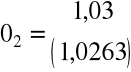
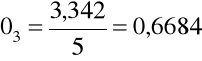
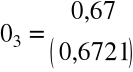
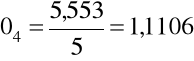
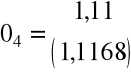
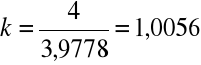
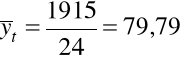
C. FUNKCJE OKRESOWOŚCI

przy czym:

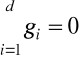
Wartość funkcji okresowości
mówi, o ile jednostek wartości zjawiska obserwowane w i-tym podokresie cyklu są na skutek wahań okresowych, przeciętnie wyższe (znak +) lub niższe (znak -) od średniego poziomu zjawiska określonego przez trend.

PROGNOZOWANIE ZJAWISK

Zjawiska z multiplikatywnymi wahaniami sezonowymi:

,

gdzie
jest wartością oszacowanej funkcji trendu dla t=T.

Zjawiska z addytywnymi wahaniami sezonowymi:

.

---