Politechnika Łódzka
Filia w Bielsku-Białej
Wydział Budowy Maszyn
Informatyka
Rok 1, Semestr 2
Grupa nr2.
ĆWICZENIE 13
Temat: Wyznaczanie przyspieszenia ziemskiego przy pomocy wahadła rewersyjnego.
Wykonali:
Korpiela Krzysztof
Krzepis Patryk
Luber Damian
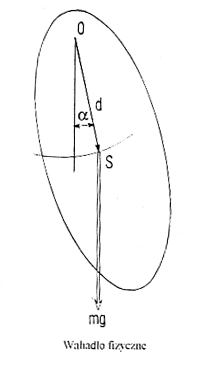
Wahadło Fizyczne - dowolne ciało sztywne, które pod wpływem własnego ciężaru wykonuje drgania wokół osi poziomej nie przechodzącej przez środek ciężkości ciała. Wychylenie wahadła o kąt ϕ powoduje, że pojawia się moment siły
![]()
![]()
![]()
usiłujący przywrócić wahadłu położenie równowagi. Wartość liczbowa tego momentu
M = -mgd sinα
gdzie m jest masą wahadła, d -odległością od punktu zawieszenia do środka masy. Stosując druga zasadę dynamiki dla ruchu obrotowego, można zapisać
I = -mgd sinα ,
gdzie I - moment bezwładności względem osi obrotu, =d2ϕdt przyspieszenie kątowe. Widać, że w ogólnym przypadku ruch wahadła fizycznego nie jest ruchem harmonicznym. Jeżeli jednak ograniczymy się do małych kątów wychylenia, to sin --> [Author:L] α ≅ α i wówczas
I*d2α/dt2 = -mgdα,
lub
d2α/dt2 = -(mgd/I)α.
Przy takim założeniu ruch wahadła fizycznego jest ruchem harmonicznym, gdyż występuje liniowa zależność między kątem wychylenia i przyspieszeniem kątowym.
Po przekształceniach otrzymujemy:
ω2 = mgd/I,
stąd okres drgań wahadła fizycznego przy niewielkich wychyleniach wyraża się wzorem:
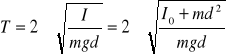
gdzie I0 jest momentem bezwładności względem przechodzącej przez środek ciężkości i równoległej do osi wahań. Okres drgań zależy od odległości między punktem zawieszenia a środkiem ciężkości. Dla bardzo małych wartości d okres jest bardzo duży. Ze wzrostem d okres drgań maleje, osiągając minimum dla d = pierwiastek(I0/m), następnie znów rośnie.
Ruch harmoniczny - ruch w którym zmieniają się: położenie, prędkość i przyspieszenie. Gdy podczas tego ruchu nie mamy strat energii i nie ma sił oporu to wówczas mamy do czynienia z drganiami swobodnymi.
Aby wywołać ruch drgający musi być spełniony warunek konieczny:
- musi działać siła harmoniczna, która jest wprost proporcjonalna do wychylenia:
F = -kx
Rys.
F = -k(x -x0) k - współczynnik proporcjonalności [N/m]
sprężystości (siła kierująca).
x
F = -kx
ma = -kx
a = dv/dt = d2x/dt2
F m(d2x/dt2) = -kx
d2x/dt2 + (k/m)x = 0
k/m = ω
0 d2x/dt2 + ω2x = 0 - równanie różniczkowe II stopnia
F
Podczas drgań torsyjnych bryły sztywnej we wzorze F = -kx siłę F trzeba zastąpić momentem siły, który można wyrazić wzorem:
M = - Dϕ.
Współczynnik proporcjonalności D o wymiarze Nm/rad nazywamy momentem kierującym. Korzystając z równania ruchu obrotowego bryły sztywnej moment siły można wyrazić wzorem:
M = Iα,
gdzie I - moment bezwładności, α - przyspieszenie kątowe, które definiuje się jako drugą pochodną kąta względem czasu:
α = ∂2ϕ/∂t2
Podstawiając ostatnie dwa wyrażenia do wzoru na moment siły otrzymujemy:
(I∂2ϕ)/∂t2 = -Dϕ
i analogicznie równanie dla drgającego punktu o masie m,
m∂2x/∂t2 = -kx.
Jeśli wprowadzimy oznaczenie ω20 = D/I lub ω20 = k/m, otrzymamy:
∂2ϕ/∂t2+ω20ϕ = 0
∂2x/∂t2+ω20x = 0
Powyższe równanie nazywamy równaniem ruchu harmonicznego prostego.
Wahadło matematyczne - punkt materialny o masie m zawieszony na nierozciągliwej i nieważkiej nici o długości l. W rzeczywistości każde wahadło musi być zbudowane w ten sposób, że nić jest nieco rozciągliwa i posiada pewną masę, a kulka metalowa zawieszona na tej nici jest większa od punktu matematycznego. Siła kierująca k jest stosunkiem siły F = mgsinα do wychylenia, które w przybliżeniu wynosi x, wtedy związek k = mgsinα/x, a dla małych wychyleń (sinα ≈ α) zachodzi k = mg/l. Podstawiając do równania:
![]()
otrzymujemy
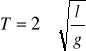
Wprowadzając do równania T = 2Π√(I0/md2)/mgd wyrazimy okres wahadła fizycznego wzorem:
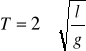
Jeśli wahadło zamocujemy w ten sposób, że będzie mogło wahać się wokół osi przechodzącej przez środek wahań, to okres wyrazi się wzorem:
T' = 2Π√(I0/md'2)/md.
Długość zredukowana będzie wyrażona wzorem:
I' = d'+I0/md,
Okres natomiast wzorem:
T' = 2Π√(l'/g).
Okresy T i T' są sobie równe, co udowodnimy poniżej. W tym celu zauważmy, że zachodzi związek l - d = d'. Różnicę l - d z tego równania można porównać z różnicą obliczoną ze wzoru l = d+(I0/md), gdzie l-d = (I0/md). Stąd otrzymujemy I0/md' = d. Podstawiając tę wielkość do równania l' = d'+I0/md,otrzymamy l' = d'+d, stąd po podstawieniu pod d' wartości z równania l-d = d' wynika związek l = l'. Równość długości zredukowanych oznacza również równość okresów T =T'.
Zatem okres oscylacji wahadła fizycznego wokół osi przechodzącej przez punkt O jest taki sam jak okres oscylacji wokół osi równoległej przechodzącej przez środek wahań O'. Za pomocą tego zjawiska można wyznaczyć wykorzystując wahadło rewersyjne przyspieszenie ziemskie.
Krótka charakterystyka pola grawitacyjnego.
Dla ciał, których rozmiary są bardzo małe w stosunku do ich wzajemnej odległości, siła oddziałująca na nie jest odwrotnie proporcjonalna do iloczynu tych mas. Można to zapisać:
F ~ m1'm2'/r2 .
Masa grawitacyjna charakteryzuje zdolność do oddziaływania grawitacyjnego z innymi ciałem. Ponieważ masa ta jest zawsze proporcjonalna do masy bezwładnej, to mówimy masa ciała i siłę grawitacyjną możemy zapisać w postaci:
F = G(m1m2/r2) ,
gdzie G jest współczynnikiem proporcjonalności zwanym stałą grawitacji. Stała G jest równa sile, z jaką przyciągają się dwa punkty materialne o masie 1 kg każdy z odległości 1 m, a jej wartość wynosi:
G = 6,67 *10-17 Nm2kg-2 .
Natężenie pola grawitacyjnego - jest to stosunek siły grawitacyjnej F przez ciało (źródło pola) o masie M i działającej na inne ciało o masie m umieszczone w polu:
γ = F/m
Natężenie pola grawitacyjnego jest liczbowo równe sile działającej w danym punkcie pola na umieszczone w nim ciało o masie jednostkowej. Natężenie pola grawitacyjnego jest wektorem, który ma kierunek, zwrot wektora siły grawitacji wywieranej przez źródło pola. Jednostką natężenia pola w układzie SI jest 1 N/kg.
γ = F/m = (GMm/R2)/m = GM/R2
Zatem natężenie w danym punkcie pola nie zależy od masy ciała w nim umieszczonego, lecz tylko od masy ciała wytwarzającego pole i od odległości tego punktu, od źródła pola. Tak więc natężenie pola charakteryzuje samo pole, a nie ciała w nim umieszczone. Stosując druga zasadę dynamiki do siły ciężkości, otrzymamy:
F = mg
gdzie F - ciężar ciała tj. siła ciążenia ciała ku Ziemi, g - przyspieszenie ziemskie.
Z wzoru γ = F/m wynika, że natężenie pola grawitacyjnego jest równoznaczne z przyspieszeniem, z jakim poruszałaby się masa, gdyby znalazła się w danym punkcie pola. Natężenie pola grawitacyjnego jest wielkością wektorową.
Potencjał grawitacyjny - to stosunek energii potencjalnej ciała umieszczonego w danym punkcie pola grawitacyjnego do masy tego ciała.
V = Ep/m
Jednostką potencjału grawitacyjnego w układzie SI jest 1 J/kg, a jego wymiarem
[V] = J/kg = (kgm2/s2)kg = m2/s2.
Wiedząc, że wartość wykonanej pracy jest równa zmianie energii potencjalnej, można zapisać:
W = Ep ⇒ W = Ep2 -Ep1,
gdzie Ep2 i Ep1 to wartości energii potencjalnych posiadanych przez ciało o masie m w punktach początkowym i końcowym. Posługując się równaniem V = Ep/m wartości tych energii można zapisać:
Ep = mV ⇒ Ep1 = mV1 i Ep2 = mV2,
gdzie V1, V2 to odpowiednio potencjały pola grawitacyjnego w punktach początkowym i końcowym. Tak więc praca związana z przeniesieniem ciał w polu grawitacyjnym między dwoma punktami dowolnie wybranymi może być wyrażona równaniem:
W = Ep2-Ep1 ⇒ W = mV2-mV1 ⇒ W = m(V2-V1).
Energia potencjalna w danym punkcie pola grawitacyjnego jest równa pracy jaką siły zewnętrzne muszą wykonać równoważąc siłę grawitacji przy przeniesieniu ciała z odległości nieskończenie dużych na odległość r. Porównując i przekształcając wymienione równania możemy ustalić od czego on zależy
W = GMm(1/R1-1/R2), W = m(GM/R1 -GM/R2)
V1-V2 = -(GM/R2-GM/R1),
Tak więc potencjał pola można wyrazić równaniem:
V =-GM/R.
Z powyższego równania wynika, iż potencjał w danym punkcie pola grawitacyjnego zależy od masy źródła pola i odległości rozważanego punktu od tego źródła.
Przebieg ćwiczenia
Celem ćwiczenia było wyznaczenie wartości przyspieszenia ziemskiego.
Schemat wahadła przedstawia rysunek.
Litery O1, O2 oznaczają osie wahadła, zaś litera M krążek.
O1
M
O2
1. Zostaje zmierzona odległość pomiędzy osiami wahadła (l=O1O2) i oszacowany błąd ![]()
l.
2. Wahadło zostaje zawieszone na ostrzu O1, a środek masy zostaje umieszczony na środku pręta.
3. Wykonano serię 10-ciu pomiarów czasu t dziesięciu drgań (n=10) bez zmiany punktu położenia masy. Wyniki zanotowano w tabeli 1 i obliczono z nich wartość średnią t, średni błąd kwadratowy pojedynczego pomiaru St' oraz błąd skorygowany przez współczynnik Studenta Fishera St.
Tab. I.
t1 [s] |
t2 [s] |
t3 [s] |
t4 [s] |
t5 [s] |
t6 [s] |
t7 [s] |
t8 [s] |
t9 [s] |
t10 [s] |
t [s] |
St' [s] |
tα,m |
St [s] |
18,78 |
18,84 |
18,82 |
18,76 |
18,87 |
18,77 |
18,82 |
18,84 |
18,80 |
18,69 |
18,80 |
0,016 |
0,95 |
0,037 |
4. Następuje seria pomiarów czasu t' 10-ciu wahnień, przy czym masa przesuwana jest od osi O1 w kierunku osi O2 o 5 cm. Wyniki zostają zanotowane w tabeli 2
5. Wahadło zostaje powieszone na drugiej osi, po czym następuje seria pomiarów czasu t" 10-ciu wahnień również przy przesuwanej masie. Wyniki zostają zanotowane w tabeli 2.
Tab. II.
kn |
[cm] |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
t' |
[s] |
20 |
19,64 |
19,23 |
19,03 |
18,84 |
18,72 |
18,64 |
18,57 |
18,61 |
18,72 |
18,90 |
18,96 |
18,98 |
19,17 |
19,39 |
19,55 |
19,83 |
19,97 |
20,29 |
t'' |
[s] |
20,15 |
19,09 |
18,28 |
17,88 |
17,65 |
17,46 |
17,30 |
17,40 |
17,57 |
17,64 |
17,93 |
18,08 |
18,41 |
18,57 |
18,83 |
19,18 |
19,61 |
19,85 |
20,31 |
6. Sporządzono wykresy t'=f(kn) i t''=f(kn) w tym samym układzie współrzędnych
7. Z wykresu tego odczytano współrzędne t'0 i t"0
8. Na podstawie uzyskanych wyników obliczono średni czas 10-ciu drgań oraz dokładność ![]()
t0, obliczono również okres drgań wahadła T0 i ![]()
t'0. Wyniki zanotowano w tabeli 3.
9. Obliczono przyspieszenie ziemskie g i błąd bezwzględny ![]()
g. Wyniki zanotowano w tabeli 3.
Tab. III.
t0' = 19,96 [s] |
t0'' = 20,26 [s] |
t0 = 20,11 [s] |
Δt0' = 0,15 [s] |
Δt0 = 0,15 [s] |
T0 = 2,01 [s] |
l = 1 [m] |
Δl = 0,005 [m] |
g = 9,76 [m/s2] |
Δg = 0,15 [m/s2] |
Obliczeń dokonano korzystając ze wzorów:
Δt'0 = |t'0-t''0|/2 = |19,96[s] - 20,26[s]| = 0,15 [s]
Δt0 = [St2+(Δt'0)2]1/2 = [(0,037[s])2 + (0,15[s])2]1/2 = 0,15 [s]
t0 = (t'0+t''0)/2 = (19,96[s] + 20,26[s])/2 = 20,11 [s]
T0 = t0/n = 20,11[s]/10 = 2,01 [s]
gobl =4Π2n2l/t02 [m/s2] = 4Π21021[m]/(20,11[s])2 = 9,76 [m/s2]
Δg = gobl{|Δl/l|+2|Δt0/t0|} = 9,76[m/s2]{|0,005[m]/1[m]|+2|0,15[s]/20,11[s]|} =
0,19 [m/s2]
St = 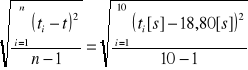
![]()
= 0,037 [s]
Wniosek:
Według obliczeń opartych na naszym badaniu, wartość przyspieszenia ziemskiego wynosi: g = 9,58 [m/s2]. Ta dość niewielka różnica pomiędzy przyspieszeniem ziemskim g ≈ 9,81 [m/s2], a wartością przez nas obliczoną może być podyktowane między innymi niedokładnością naszych pomiarów (zbyt wczesne lub zbyt późne uruchamianie, zatrzymywanie stopera).
Korekta błędów, którą trzeba dokonać dotyczy:
zastąpienia st na st'
zapisania st=tα;n -st'
skorygowania wartości w tabeli, obl.Δg
11
ĆWICZENIE NR 13
WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO PRZY POMOCY WAHADŁA REWERSOWEGO
![]()
![]()
![]()
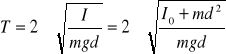
![]()
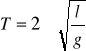
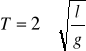
Wyszukiwarka