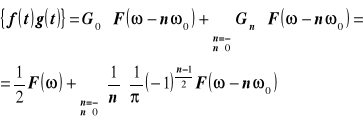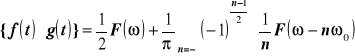
WPROWADZENIE DO SYSTEMÓW TELEKOMUNIKACYJNYCH

SEMINARIUM

Piotr Zaniewski

Prowadzący :

Dr inż. W. Krzysztofik

Zadanie Z1/16

Korzystając z twierdzenia o splocie w dziedzinie częstotliwości wyprowadzić wzór na transformatę Fouriera iloczynu dowolnej funkcji f(t) i funkcji okresowej g(t). Opierając się na wyprowadzonej zależności udowodnić, że

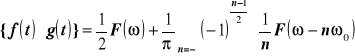
Rozwiązanie :

Splot w dziedzinie częstotliwości określony jest wzorem :

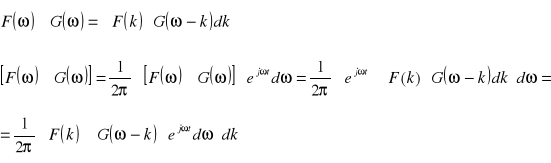
Dokonuję zamiany zmiennych w całce wewnętrznej podstawiając ω-k = u

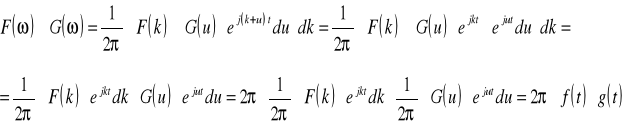
Szukam G(ω)

Ponieważ g(t) jest okresową funkcją czasu , stąd

gdzie (*)

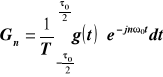
czyli otrzymuję :

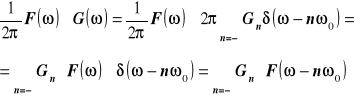
Na podstawie własności :

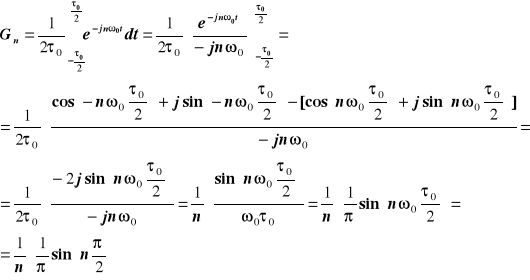
Wyznaczam G_n na podstawie wzoru (*) .

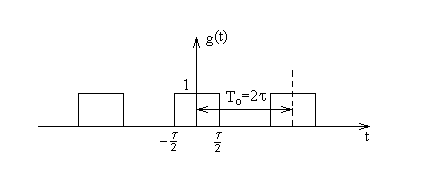
Zgodnie z wykresem funkcji g(t) mam, że :

T = 2τ₀ i ponieważ Tω₀ = 2π

otrzymuję zależność :

ω₀ τ₀ = π

Obliczam wartość G_n dla n = 0

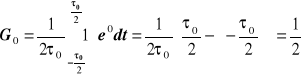
Obliczam wartość G_n dla n = 0

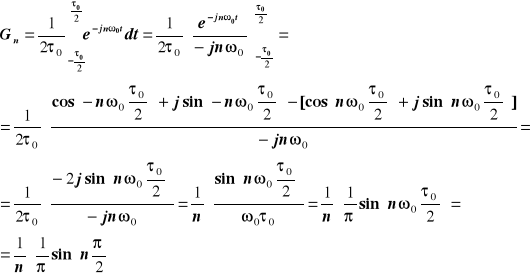
Dla n = ... ,-5 ,-1 ,3 ,7 ,11 ,... sin(nπ/2) = -1

n = ... ,-3 ,1 ,5 ,9 , ... sin(nπ/2) = 1

dlatego

czyli ostatecznie otrzymuję :

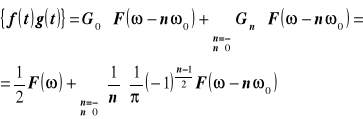
co było do udowodnienia .
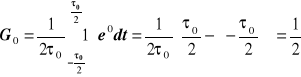
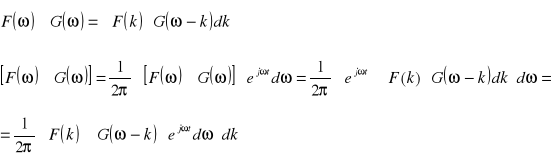
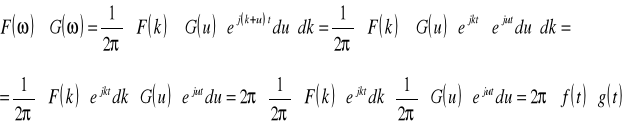
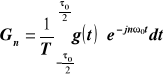
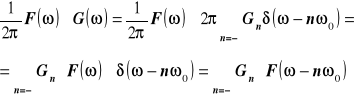
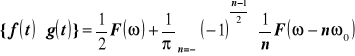