Matematyka dyskretna. Zadania domowe 2.

1. Dla dwóch permutacji

1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9

f = g =

7 8 5 2 9 3 4 1 6 9 8 7 6 5 4 3 2 1

1. wyznacz ich złożenie fg

2. wyznacz permutacje odwrotne

3. rozłóż je na cykle i określ ich typ

4. wyznacz znak permutacji f, g, poprzez wyznaczenie liczby inwersji

5. sprawdź prawdziwość wzoru sgn(fg) = sgn(f) · sgn(g)

2. Wyznacz znak permutacji przy pomocy wzoru, wykorzystującego liczbę cyklów o długości parzystej:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

f =

14 7 10 6 5 8 15 13 2 1 12 3 4 11 9

Rozłóż permutację f na transpozycję.

3. Rozłóż permutacje na transpozycje i sprawdź poprawność rozkładu:

1 2 3 4 5 6

f = = [4 5] [2 3] [1 6]

6 3 2 5 4 1

4 Na ile sposobów może 8 osób wysiąść na trzech piętrach z windy, jeżeli uwzględniamy kolejność wysiadania ?

5. Do zdania egzaminu potrzeba więcej niż 50% punktów. Tworzymy dwie listy - tych osób, które zdały egzamin i tych które nie zdały, w kolejności otrzymanych punktów. Wiedząc, że w grupie 10 studentów żaden wynik nie powtórzył się, oblicz ile jest możliwych rozmieszczeń tych 10 osób na dwóch listach.

6. a) Jaka jest najmniejsza moc relacji równoważności w zbiorze 6-elementowym?

b) czy istnieje relacja rownowaznosci o mocy równej 7 w tym zbiorze?

3. Jaka jest największa moc relacji częściowego porządku w zbiorze 3-elementowym?

7. Oblicz ilość różnych harmonogramów wykonywania pięciu programów na trzech procesorach oraz ilość różnych harmonogramów wykonywania trzech programów na pięciu procesorach. Jeden program przyporządkowujemy tylko jednemu procesorowi. Za różne uważamy harmonogramy, w których inny jest przydział programów do procesorów lub inna jest kolejność ich wykonywania. Która z obliczonych liczb jest większa i ile razy?

8. Ile jest permutacji 10-elementowych, w ktorych rozkładzie na cykle rozłączne wystąpi

cykl 9-elementowy?

9. Oblicz ile wynosi współczynnik liczbowy przy wyrazie x² y⁵ w rozwinięciu dwumianu (x - 2y)⁷ .

10. Na ile sposobów można wybrać z 20 osób 3 rozłączne zespoły liczące odpowiednio 3, 5 i 7 członków?

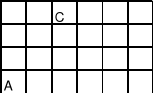
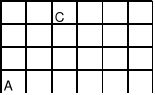
11. Ile jest najkrótszych dróg na podanym planie miasta:

które prowadzą z punktu A do B i nie przechodzą przez punkt C?

12. Ile różnych liczb 7 cyfrowych można utworzyć, zapisując w dowolnej kolejności 7 cyfr 8, 8, 8, 8, 5, 5, 2 ?

13. Wykazać tożsamość:

Σ (-1)r = 0 n ∈ N, n > 0

14. Ile jest rosnących ciągów czterowyrazowych o możliwych wartościach 1, 2, 3, 4, 5, 6, 7?

• B

•

•

r =0

n

---