Def.Superpozycją (złożeniem) odwz. f:X→Y i g:Y→Z nazywamy takie odwz. g°f:X→Z , które spełmia warunek ∀x∈X (g°f)(x)=g[f(x)]
Def.Jeżeli spełniony jest warunek ∃e∈A ∀a∈A e#a=a#e=a to element e nazywamy elementem neutralnym, a półgrupę - unitarną.
Def.Półgrupę unitarną komutatywną, w której każdy element ma element symetr., tzn. ∀A ∃a'∈A a#a'=a'#a=e nazyw. grupą abelową.
Def.Trójką (A,#,°)[gdzie #,°-dwa działania wewnętrzne w niepustym zbiorze A] spełniającą warunki:1.para (A,#)- jest grupą abelową
2.para (A,°)- jest półgrupą 3. działanie „°” jest dystrybutywne ( rozdzielne ) względem działania „#” tzn. ∀a,b,c∈A (a#b)°c=(a°c)#(b°c) c°(a#b)=(c°a)#(c°b) nazywamy pierścieniem.
Def. ciałaPierścień całkowity, w którym każdy element niezerowy ma element symetryczny (względem drugiego działania) nazywamy ciałem. Elementy ciała nazywamy liczbami albo skalarami.
Def. przestrzeni liniowej (wektorowej)Niech V=(A,+) [będzie grupą abelową], K dowolnym ciałem zaś S:K×V→V odwzorowaniem, które parze elementów (α,V)∈ K×V będziemy oznaczać S(α,V)=αV. Trójkę (V,K,S), która spełnia warunki:1.∀α∈K ∀a,b,c∈V α(a+b)=αa+αb 2.∀α,β∈K ∀a∈V (α+β)a=αa+βa
3.∀α,β∈K ∀a∈V (αβ)a=α(βa) 4.∀a∈V 1a=a - nazywamy przestrzenią liniową, przestrzenią wektorową nad ciałem K i oznaczamy symbolem V(K). Elementy grupy V nazywamy wektorami, a odwzorowanie S, mnożeniem skalarów przez wektory.
Tw. d'Alamberta Każdy wielomian w dziedzinie zespolonej stopnia n≥1 ma co najmniej jedno miejsce zerowe.
Wielomiany w liczbie zespolonej
Jeżeli liczba zespolona z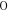
jest pierwiastkiem wielomianu p o wspólczynnikach rzeczywistych, to również pierwiastkiem tego wielomianu jest liczba sprężona 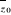
.
![]()
![]()
![]()
![]()