Egzamin PP rok 1 Transport dzienne i zaoczne: kwestie zdane na egzaminie pisemnym w poniedziałek 1-ego i wtorek 2-ego oraz w sobotę 6-ego lutego 2010 roku

zestaw A

A1. Naszkicuj krzywe określone równaniem

  y = 4⋅sinc(x) w układzie ortokartezjańskim Oxy,

  r = 4⋅sinc(θ), gdzie r i θ są współrzędnymi w układzie biegunowym Orθ, 0 ≤ θ ≤ 3π.

A2. Podaj definicję brachistochrony i przedstaw jej związek z cykloidą.

A3. (s) Sprawdź, że zbiór V wektorów rzeczywistych trzywymiarowych ze standardowymi dodawaniem (+) i skalowaniem (∗) liczbami rzeczywistymi jest przestrzenią liniową.

A4. Płaską płytkę kwadratową o pomijalnej grubości wykonano z jednorodnego materiału, o ciężarze właściwym ρ Oblicz jej moment bezwładności względem jej środka, gdy bok płytki ma długość 2a. Wyraź ten moment wzorem, w którym występuje masa m tej płytki.

A5. (s) Oblicz kąt α, jaki tworzą ze sobą proste U i V, gdzie U : x = t, y = 2t, z = t;

V : x = 0, y = t, z = t.

A6. (s) Oblicz wyznacznik macierzy Dürera.

-----------------------------------------------------------------------------------------------------------------

zestaw B

B1. Uzyskaj równanie funkcji odwrotnej do funkcji, której wykres nazywamy standardową krzywą łańcuchową.

B2. Podaj definicję mechaniczną kardioidy. Naszkicuj wykres kardioidy.

Przedstaw, jak kardioida pojawia się w optyce

B3. (s) Napisz, jakim wzorem określił Steinitz równość (~) w zbiorze S := { (p, q) : p ∈ Z; p ∈ N }. Sprawdź, że ta równość jest relacją równoważności.

B4. Oblicz pole P obszaru, jaki ograniczają krzywe o równaniach y = 1/( 1 + x² ) i y = x²/2.

B5. (s) Wyznacz punkt Q, w którym płaszczyznę Oxy przebija prosta przechodząca przez punkt P = (4, 5, 6) i prostopadła do płaszczyzny x - y + z - 1 = 0.

B6. (s) Oblicz wartości własne macierzy B = 
.

-----------------------------------------------------------------------------------------------------------------

zestaw C

C1. Naszkicuj krzywe określone równaniem

  y = cos²(x), gdzie x, y są współrzędnymi w układzie ortokartezjńskim Oxy,

  r = cos²(θ), gdzie r i θ są współrzędnymi w układzie biegunowym Orθ, 0 ≤ θ ≤ 3π.

C2. Podaj definicję mechaniczną asteroidy. Naszkicuj wykres tej krzywej.

Przedstaw sytuację inną niż mechaniczna, w której powstaje asteroida.

C3. (s) Niech M :=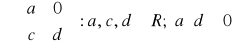 
.

Sprawdź, że zbiór M stanowi grupę ze względu na mnożenie w sensie Cauchy'ego.

C4. Oblicz objętość V bryły, która powstaje w wyniku obrotu wokół osi poziomej Ox krzywej o równaniu y = 
.

C5. (s) Wyznacz wektor w prostopadły do wektorów u = [ 1, 2, 6 ]^T i v =  [ 0, 1, 2 ]^T taki, że w ma długość równą 1 i że trójka (w, u, v) jest zorientowana ujemnie.

C6. (s) Napisz o zagadnieniu transportowym:

  a) jakie są w nim dane,

  b) co jest szukane,

  c) jaki pojawia się w nim ural.

Utwórz ten ural, gdy liczba nadawców S = 4, liczba odbiorców D = 3.

Z1. Opisz przejście z układu współrzędnych biegunowych Orθ do układu współrzędnych kartezjańskich Oxy i na odwrót. Rzecz zilustruj rysunkiem.

Z2. Napisz, co to jest brachistochrona, i podaj jej związek z cykloidą.

Z3. Wyznacz przedziały, w których funkcja f, gdzie f(x) := x³ - x² - x - 1 jest wypukła.

Z4. Z materiału o ciężarze właściwym ρ wykonano płaską płytkę o pomijalnej grubości, szero-kości 7 cm i długości 30 cm. Oblicz jej moment bezwładności względem dłuższego boku.

Z5. Rozwiąż ural A⋅x = b, gdy A := 
, b := 
. Odp. x =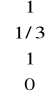 
.

Z6. (C6) Napisz o zagadnieniu transportowym: a) jakie są w nim dane (i w jakiej formie się je zapisuje), b) co jest szukane, c) jaki pojawia się w nim ural ze względu na poszukiwane wielkości.

-----------------------------------------------------------------------------------------------------------

U1. Wymień klasyczne ciała liczbowe i wskaż równania, które w jednym z nich mają rozwiązanie, a w innym nie mają.

U2. Naszkicuj linię łańcuchową, podaj jej równanie i uzyskaj pochodną funkcji wyznaczającej krzywą łańcuchową.

U3. Wyznacz wielomian w Maclaurina stopnia 3 dla funkcji y = f(x), gdzie f(x) = ln(1 + x), i sporządź, na jednym rysunku, wykresy tej funkcji i tego wielomianu.

U4. Naszkicuj wykres krzywej Gaussa (zwanej też krzywą rozkładu normalnego), zapisz jej równanie y = f(x) i uzyskaj pochodną f `(x).

U5. Oblicz moduł i argument liczby z = 
.

U6. Wyznacz rozwiązanie y = y(x) równania y''- y = 0 takie, że y(0) = 1.

                       

Każdy, kto nie potrafi udzielić poprawnych odpowiedzi na wszystkie ww. pytania,

najprawdopodobniej na egzaminie poprawkowym

(15.lutego 2010 - studia dzienne,

20.lutego 2010- studia zaoczne)

uzyska ocenę ndst.

Na egzaminie poprawkowym student(ka) może zrezygnować, nie uzyskując oceny ndst, z odpowiedzi w ciągu pierwszych 10 minut trwania tego egzaminu (przy tym musi pisemnie zadeklarować, iż rezygnuje z egzaminu w tym terminie).

Egzamin 2010-02-15

D1. (B1) Uzyskaj równanie funkcji odwrotnej do funkcji, której wykres nazywamy standardową krzywą łańcuchową.

D2. (U3) Wyznacz szereg T i wielomian w Maclaurina stopnia 3 dla funkcji y = f(x), gdzie f(x) = ln(1 + x), i sporządź, na jednym rysunku, wykresy tej funkcji i tego wielomianu.

D3. Oblicz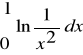
. .

D4. (s) Sprawdź, czy są do siebie podobne macierze A :=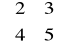 
i B :=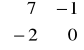 
.

D5. Uzyskaj rozwiązanie y = y(x) równania y'' + y = 0 takie, że y(0) = 1.

--------------------------------------------------------------------------------------------------------------

E1. (Z4) Z materiału o ciężarze właściwym ρ wykonana została płaska płytka o pomijalnej grubości, szerokości 7 cm i długości 30 cm. Oblicz jej moment bezwładności względem dłuższego boku.

E2. (s) Wyznacz równanie płaszczyzny prostopadłej do wektora u = [ 3, 4, 5 ]^T i przechodzą-cej przez punkt P =  (-3, 2, 1). Odp. 3x + 4y + 5z = D, D = 3⋅(-3) + 4⋅2 + 5⋅1 = 4. 

E3. Podaj dwa różne określenia hiperboli i jej równania.

E4. (≈A5,s) Oblicz kąt α, jaki tworzą ze sobą proste U i V, gdzie U : x = t, y =   2t, z = t; V : x = 3, y = 3+t, z = t.

E5. (s) Napisz tabelkę Cayleya na mnożenie pierwiastków 4-tego stopnia z 1 i pokaż,że zbiór tych pierwiastków wraz z mnożeniem stanowi grupę.

------------------------------------------------------------------------------------------------

F1. (U6) Wyznacz rozwiązanie y = y(x) równania y''- y = 0 takie, że y(0) = 1.

F2. (B5,s) Wyznacz punkt Q, w którym płaszczyznę Oxy przebija prosta przechodząca przez punkt P = (4, 5, 6) i prostopadła do płaszczyzny x - y + z - 1 = 0.

F3. (s) Rozwiąż ural A⋅x = b, gdy A := 
, b := 
.

F4. Oblicz powierzchnię, jaką ograniczają półprosta θ = π i łuk o równaniu θ² - r² = 1, gdy r, θ są współrzędnymi biegunowymi ( r ≥ 0, -π < θ ≤ π).

F5.   (s) Wyznacz wartości i wektory własne macierzy obrotu płaskiego o 30°. Otrzymany wynik zinterpretuj w terminach kierunków własnych/głównych obrotu.

-----------------------------------------------------------------------------------------------

2010-02-01 kwestie zadane na egzaminie 3/3

---