25. Szereg trygonometryczny Fouriera. y=f (x) w <a,b>

sz. Fouriera wzór Fouriera

{1,cosx,sinx,cos2x,sin2x,...,cosnx,sinnx,...}

Tw. Układ funkcji trygon. będzie ortogonalny

{1,cosx,sinx,...} jest ortogonalny w <-π,π>

całka tych funkcji będzie zero:

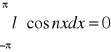
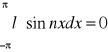
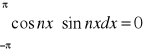
szereg trygon. Fouriera y=f(x) <-π,π> wzór ogólny:

wzory Eulera-Fouriera

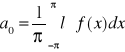
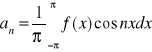
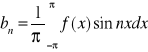
C₀=2a₀ C_2n-1=a_n C_2n=b_n

Tw. Jeżeli szereg trygon. jednostajnie zbieżny w <-π,π> do f(x)=>