Drgania tłumione układu o jednym stopniu swobody wymuszone siłą harmonicznie zmienną

Siła wymuszająca drgania

Równanie ruchu

stąd równanie różniczkowe drgań wymuszonych nietłumionych

Częstość kołowa drgań własnych masy
,
,

Rozwiązanie równania jest równe sumie rozwiązania ogólnego równania jednorodnego oraz rozwiązania szczególnego

gdzie
rozwiązanie szczególne

Po podstawieniu wyrażenia x₂ do równania ruchu otrzymamy amplitudy drgań wymuszonych A

grupując wyrazy wg
i
otrzymamy
równanie to będzie spełnione tożsamościowo gdy współczynniki przy sinΩt i cosΩt będą równe zeru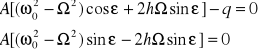

stąd
(ε -kąt opóźnienia w fazie względem siły wymuszenia P(t) ) oraz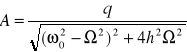

Zatem poszukiwanym rozwiązaniem ruchu będzie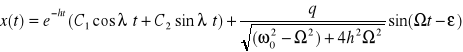

Wzór na amplitudę drgań można przekształcić do postaci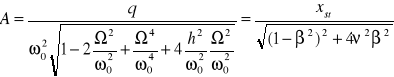

Gdzie
,
,

Do analizy drgań wprowadzono współczynnik uwielokrotnienia amplitudy (współczynnik amplifikacji)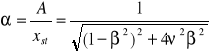

Tłumienie ma bardzo istotny wpływ na wartość kata przesunięcia fazowego miedzy amplituda a siłą wymuszająca

Na rysunku pokazano przebiegi charakterystyki amplitudowo-częstotliwościowej i fazowo-częstotliwościowej

ϕ

β

α

c

m

k

P(t)

β

1

0

90°

180°

1

0

1