* Drgania oscylacyjne prądu w ukł. szer. R, L i C zasilonym napięciem w postaci skoku jednostkowego ε(t) wystąpią przy:

a) R=1Ω; L=1H; C=1F; c) R=1Ω; L=4H; C=1F;

*Sygnał u(t)=ε(t)-ε(t-T) ma transformatę Lapalce'a:

d) U(s)=(1/s)[1-exp(-sT)]

* Charakterystyka częstotliwościowa sygnału napięciowego u(t)=ε(t)-ε(t-T) dana jest zależnością:

d) U(jω)=1/jω*(1-exp(-jωT));

* Nap. na kondensat. w ukł szer. RC, zasilanym nap. w post. impulsu Diraca, ma post.:

?) Uc(t)=1/RC*exp(-1/RC)

* W obwodzie: źródło napięcia stałego E, opornik R i cewka L zostaje w chwili t=0s zamknięty łączniik. Przebieg napięcia na oporniku dany jest : c) u_R(t)=E(1-exp(-R/L*l);

* W obw. Szereg. E=1v, R=1Ω, L=1H, C=1F macierz ukł. : A=[-R/L; -1/L]

[ 1/C; 0 ]

* Transmitancja ukł. cyfrowego H(z)=1/(1+3z^-1+2z^-2) odpow. równ.: d) y[n]=x[n]-3y[n-1]-2y[n-2]

* Pojemność jednostkowa przewodu symetrycznego o prom. a=1mm i odległ. między dr. d=5mm w powietrzu (μ₀=1,256μH; ε₀=8.85 pF/m) wynosi:

d)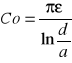
e) C₀=17,3 pF/m ;

* Pojemność jednostkowe przewodu o prom. a=1mm w odległ. h=5mm od płyty uziemionej w powietrzu (μ₀=1.256μH/m; ε₀=8.85pF/m) wynosi:

B) C₀=24,15pF/m; D)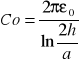

* Pojemność jednostkowa przewodu symetrycznego o promieniu drutu a=1mm, odległości między drutamid=5mm w powietrzu (μ₀=1.256μH/m; ε₀=8.85pF/m) wynosi:

D)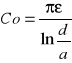
E) Co=17,3pF/m

* Indukcyjność jednostkowa przewodu. o prom. a=1mm w odleg. h=5mm od płyty uziem. w pow. (μ₀=1.256μH/m; ε₀=8.85pF/m) :

B)
C) L₀=0,461uH/m;

* Impedancja Fal. przewodu o prom. a=1mm

w odleg. h=5mm od płyty uziem. w powietrzu (μ₀=1,256μH; ε₀=8.85 pF/m) wynosi:

b)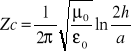
c) Zc=138Ω;

* Impedancja Fal. przewodu symetrycznego o prom. a=1mm w odległ. między drutami d=5mm w pow. (μ₀=1.256μH/m; ε₀=8.85pF/m) wynosi: A)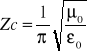
C) Zc=193Ω;

* Imped. falowa stratnej linii transmis. dana jest zależnością: A) Zc= √{[Ro + jωLo ]/[Go + jωCo ]};

E) Zc=⁴√{[Ro²+(ωLo)²]/[Go²+(ωCo)²]};

* Impedancja Wej. linii bezstr. zwartej na końcu :

a) Z₂=-jZ_cctg(βl)

* Impedancja Wej. lini bezstr. zwartej na końcu :

B) Z₂=jZ_ctg(ω/v*l); E) Z₂=jZ_ctg(2π*l/λ);

* Impedancja Wej. linii bezstr. w stanie jałowym :

B) Zo=-jZ_Cctg[(ω/v)l]; E) Zo=-jZ_Cctg[2π(l/λ)];

* Górnoprzepustowy pasywny filtr RC ma transmitancję częstotliwościową:

E) H(jω)=(jωRC)/(1+jωRC)

**RC* H(ω)={(ωRC)/√[1²+(jωRC)²]}

ϕ(ω)=-arctg(ωRC)

L(ω)=-10logH(ω)

**CR* H(ω)={(1)/√[1²+(ωRC)²]}

ϕ(ω)=(π/2)-arctg(ωRC)

L(ω)=20logH(ω)

Układ szeregowy RC:

Załączenie źródła napięcia stałego:

E=u_R(t)+u_C(t);

u _R(t)=Ri(t); i(t)=C(du_C(t)/dt);

(du_C(t)/dt)+(1/RC) u_C(t)=E/(RC);

u_C(t)=U(1-e^{-t/(τ)}; τ=RC;

u _R(t)=E-u_C(t)=Ee^{-t/τ}; i(t)=( u _R(t)/R)= (E/R)e^{-t/τ};

Załączenie źródła napięcia sinusoidalnego:

Z=√(R²+(1/(ωC))²); ϕ=arctg(1/(ωRC));

u(t)=( E_m/(ωCZ)){-cos(ωt+ψ+ϕ)+cos(ψ+ϕ)e^{-t/(RC)}};

Układ szeregowy RLC:

Załączenie źródła napięcia stałego:

E=u _R(t)+u_L(t)+u_C(t); i(t)=C(du_C(t)/dt);

u _R(t)=Ri(t); u_L(t)=L(di_L(t)/dt);

(d²u_C(t)/dt²)+(R/L)(du_C(t)/dt)+(1/LC)u_C(t)=E/(LC)

Metody częstotliwościowe :

Podstawowe własności przekształcenia Laplace'a:

F(s)=₀∫^∞ f(t)exp(-st)dt; s=σ+jω;

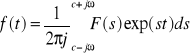
Charakterystyki częstotliwościowe sygnałów:

F(jω)=f(ω)exp[jϕ(ω)]

Transmitancja częstotliwościowa: Y(jω)= H(jω)X(jω)

Charakterystyki amplitudowa i fazowa: H(jω)=H(ω)exp[jϕ(ω)]; Ch. Amplitudowo-fazowa: H(jω)=P(ω)+jQ(ω)];

Ch. Naturalna logarytmiczna amplitudowa: L(ω)=lnH(ω), [Np]

Logarytmiczna ch. Amplitudowa: L(ω)=20lgH(ω), [dB]

Dla filtra dolnoprzepustowego RC:

Y(jω)=(1/(1+jωRC))X(jω); H(jω)=(1/(1+jωRC))

Ch.A.: H(ω)={1/[√(1+(ωRC)²)]};

Ch.F.: ϕ(ω)=-arctg(ωRC)

Ch.L.A.: L(ω)=-10lg{1+[ω/(ω_gr­)]²} ω_gr=1/(RC)

Dla filtra górnoprzepustowego RC:

Y(jω)=(1ωRC/(1+jωRC))X(jω); H(jω)=(1+jωRC/(1+jωRC))

Ch.A.: H(ω)={ωRC /[√(1+(ωRC)²)]};

Ch.F.: ϕ(ω)=(π/2)-arctg(ωRC)

Ch.L.A.: L(ω)=20lg{(ω/ω_gr)/√[1+(ω/ω_{gr ­})²]}

Przekształcenie Z :

Sygnał dyskretny	Transformata Z	Promień zbieżności
F[n]=δ[n]={1 dla n=0 {0 dla n>0	F(z)=1	R0=0
F[n]=δ[n-k] , n≥0	F(z)=z^-k	R0=1
F[n]=ε[n]=1, n≥0	F(z)=z/(z-1)	R0=1
F[n]=a^n, n≥0	F(z)=z/(z-a)	R0=a

Transmitancja układu cyfrowego:

dla: y[n]+a₁[n-1]=b₀x[n]+b₁x[n-1];

to po: Y(z)(1+a₁z^-1)+a₁y[-1]=X(z)(b₀+b₀z^-1);

jest zależność: Y(z)=( b₀+b₀z^-1)/(1+a₁z^-1)X(z)+(-a₁y[-1])/( 1+a₁z^-1)

i funkcja: H(z)= ( b₀+b₀z^-1)/(1+a₁z^-1)

1) Transformaty Laplace`a [f(t) ; F(t)]

a) (t) ; 1/s	b (t  s
c) (t -T) ; (1/s)*e^-sT	d) e^-^^t(t  (s+)
e) sin(t) ; /(s^2 + ^2)	f) cos(t) ; s/(s^2+ ^2)
g) e^-^^t sin(t) ; /[(s + )^2+ ^2]

2) Górnoprzepust. Pas. filtr RC ma transmit. Częstotl.

K(j)=jRC/(1 + jRC) ; |K(jRC/√1+(RC)²

a dolnoprzepustowy : K(j) = 1/(1 + jRC);

|K(j√(RC)²; pulsacja gran: =1/RC

Dolnoprzepustowy LR : K(j)=R/(R + jL)

8) Przewód symetryczny :

d- odl.między drutami, a- promień drutu

Indukcyjność jednostkowa Lo= ( / )* ln (d/a)

Pojemność jednostkowa Co=  / ln(d/a)

Impedancja falowa Zc =(1/)*√( / )ln(d/a)

Przewód nad ziemią:

h- odl.od ziemi , a- promień drutu

Lo= (/2)ln(2h/a) Co=(2a)/ln(2h/a)

Zc= (1/2)*√( / )ln(2h/a)

Kabel koncentryczny(współosiowy):

Lo= (/2)ln(d/a) Co= (2)ln(d/a)

Zc= (1/2)*√( / )ln(d/a)

9) Linia stratna:

Impedancja falowa Zc =√(Ro+jLo)/(Go+jCo)

Współczynnik przenoszenia

γ =√(Ro+jLo)(Go+jCo)= j

10) Linia bezstratna (z_C bez j)

Ro=0 i Go=0 γ =j√LoCo ;

0 ; =√LoCo = /v = 2/

Zc=√(Lo/Co) =v/f ;=0

cosh γ L=cosL sinh γ L= j*sinL

Z_we=Z_c*{[(Z_obc*ch[γ(s)*l)+Z_c(s)sh[γ(s)*l]}

/{[(Z_obc*sh[γ(s)*l)+ch[γ(s)*l]}

U₁=U₂*cosL+jZcI₂*sinL

_ jU₂Zc*sinC+I₂*cosL

W stanie jałowym:

Impedancja wejściowa: Zz= -jZc*ctgL ;

U₁=E/s U₂= U₁/(ch(s*l/v))

W stanie zwarcia:

Impedancja wejściowa: Zz= jZc *tgL

11) Linia niezniekształcająca:

γ = (√RoGo ) + j(√LoCo) Zc=√(Lo/Co); V=√L₀C₀

=√RoGo , =√LoCo =l/v -czas propagacji

12) Napięcie źródła w mod. komp. cewki (Euler):

e_L[k]= -R_Li[k - 1] ,R_L=L / h

Inne wzory dla cewki: u_L[k]=R_Li[k]+e_L[k]

G_L=1/R_L =h/L j_L[k]=- i[k-1]

Wzór trapezów: ( u_L[k]+u_L[k-1] )/2=L[(i[k]-i[k-1] )/h]

Wzór Eulera: u_L[k]=(L/h)*i[k]- (L/h)*i[k-1]

13)Napięcie źródła w mod.komp. Kondensat.(Euler):

e_C[k]=u_C[k-1]+Rc*i[k-1] ,Rc=h/2C

Wzór Eulera: u_C[k]=(h/C)*i[k]+u_C[k-1]

i[k]= C*[(u_C[k]-u_C[k-1] )/ h]

Wz. trapezów: (i[k]+i[k-1] )/2=C*(u_C[k] - u_C[k-1] )/h)

---