WSTĘP TEORETYCZNY

Galwanometr jest elektrycznym przyrządem pomiarowym, najczęściej magnetoelektrycznym, służącym do pomiaru bardzo małych napięć i natężeń prądu elektrycznego. Ze względu na konstrukcję można wyróżnić galwanometry z ruchomym magnesem obracającym się w polu magnetycznym prądu nieruchomej cewki oraz galwanometry z ruchomą cewką w polu nieruchomego magnesu. W praktyce laboratoryjnej są używane prawie wyłącznie galwanometry drugiego typu.

W galwanometrach tego typu cewka w kształcie ramki może obracać się w szczelinie między nabiegunnikami magnesu NS i cylindrycznym rdzeniem R wykonanym z magnetycznie miękkiego żelaza. Dzięki rdzeniowi pole magnetyczne w szczelinie jest radialne i w przybliżeniu ma prawie wszędzie jednakowe natężenie. Takie ukształtowanie pola w szczelinie sprawia, że siła F z jaką pole magnetyczne działa podczas przepływu prądu przez cewkę na pionowe boki ramki i powoduje jej obrót, jest w każdym położeniu cewki stała i prostopadła do jej płaszczyzny. Siła F wyraża się wzorem.

F = n I a B gdzie: n - liczba zwojów cewki

I - natężenie prądu

a - wysokość ramki

B - indukcja magnetyczna

Ponieważ siła jest niezależna od położenia ramki, także moment skręcający Ms jest stały i nie zależy od kąta  określającego położenie ramki (dla  = 0 ramka jest w położeniu równowagi, nie przepływa przez nią prąd).

Ms = b F = n I A B - gdzie: b - szerokość ramki

A - powierzchnia ramki

Przeciwstawia się temu moment siły związany ze skręcaniem sprężystej nici, jego wielkość jest proporcjonalna do kąta obrotu

Mk = k 

W warunkach równowagi oba te momenty są równe

k   n I A B

czyli kąt o który obróci się ramka zależy od natężenia przepływającego prądu

  n I A B / k

Jeżeli w pewnej chwili przerwiemy obwód zasilający cewkę galwanometru, zniknie moment skręcający, a moment związany z siłami sprężystości nici zgodnie z drugą zasadą dynamiki dla ciał w ruchu obrotowym, nada cewce przyspieszenie. Po odłączeniu źródła prądu, gdy cewka wraca do punktu równowagi porusza się w polu magnetycznym. Zgodnie z prawem indukcji Faradaya w ramce indukuje się prąd przeciwstawiający się temu ruchowi. Całkowity moment hamujący jest równy

MH = - ( n A B )2 / Rg+ Rz * ( d  dt )

gdzie : Rg - opór galwanometru

Rz - opór obwodu, do którego podłączony jest galwanometr czyli:

  Mk + MH / J

Przekształcając to w postać różniczkową otrzymujemy równanie zwane równaniem różniczkowym ruchu harmonicznego tłumionego

d2  dt2 + 2d  dt + 

gdzie:  - kąt odchylenia ramki

2  współczynnik tłumienia drgań

Rozwiązaniem tego równania jest funkcja

(t) = e- t A sin (  t + δ 

Stałe A, δ mogą być określane z warunków początkowych. Wyrażenie A*e- t spełnia rolę amplitudy drgań, która w przeciwieństwie do ruchu harmonicznego prostego nietłumionego nie jest stałą w czasie, lecz maleje wykładniczo, stąd zrozumiałym staje się nazwanie  współczynnikiem tłumienia. Ruch, jaki wykonuje cewka zależy od tego, jak duży jest ten współczynnik. Gdy przyjmuje duże wartości mamy do czynienia z ruchem aperiodycznym, gdy małe - z tłumionym.

Szybkość zmiany amplitudy często przedstawia się za pomocą tzw. logarytmicznego dekrementu tłumienia. Określa się go z zależności

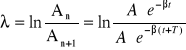
Logarytmiczny dekrement tłumienia charakteryzuje tłumiony obwód drgający, jest stały w czasie i określa, jak zmienia się amplituda drgań po czasie równym okresowi drgań tłumionych.

OPIS UKŁADU POMIAROWEGO

Wychylenie galwanometru przy zamkniętych kluczach K1 i K2 zależy od oporności R oraz różnicy napięć między punktami A i B, regulowanej przez dzielnik napięcia (składnik Rn/Rn+R1)

Po rozwarciu klucza K1 pod wpływem momentu skręcającego nici Ms cewka galwanometru rozpocznie ruch do położenia równowagi, a ponieważ znajduje się w polu magnetycznym, popłynie przez nią prąd indukcyjny w takim kierunku, że przeciwdziała ruchowi ramki wywołując moment hamujący MH. Opornością R można regulować współczynnik tłumienia  od bardzo dużej wartości do zera.

---