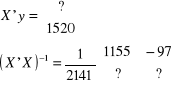
ZADANIA Z ROZWIĄZANIAMI

Zadanie 1

Oszacuj modelu popytu na produkt ABC w zależności od ceny tego produktu, gdzie Y - popyt (w tys. sztuk), X - cena (w zł). Na podstawie 10 obserwacji otrzymano następujące wyniki:

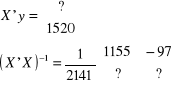
SKR = 7,732,

OSK = 1881,6

Oszacuj parametru modelu liniowego, oceń dopasowanie modelu do danych empirycznych oraz zbadaj istotność zmiennej objaśniającej na poziomie istotności 0,05.

Rozwiązanie:

Macierz CROSS jest macierzą symetryczną oraz mamy informację odnośnie liczby obserwacji, zatem:

W macierzy X'y pole ze znakiem zapytania odpowiada zgodnie z układem CROSS sumie Y -
.

Mamy informacje dotyczącą ogólnej sumy kwadratów, zatem korzystając ze wzoru na OSK obliczam sumę Y:

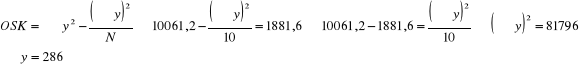
Zatem:

Wyznaczam parametru modelu:

Model ma postać:

• jeżeli cena wzrośnie o 1 zł, to popyt zmaleje o około 5,86 tys. sztuk

• dla ceny zerowej potencjalny popyt wynosi 85,42 tys. sztuk.

Ocena dopasowania modelu do danych empirycznych:

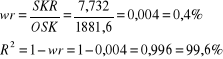
99,6% ogólnej zmienności popytu jest wyjaśniane przez model. Dopasowanie do danych empirycznych jest na bardzo wysokim poziomie.

Badanie istotności zmiennej objaśniającej:

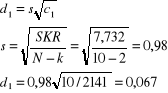
Obliczam wartość statystyki t-Studenta:

Wartość krytyczna odczytana z tablic rozkładu Studenta dla ośmiu stopni swobody i poziomu istotności wynosi 2,306.

Ponieważ:

Zmienna X jest statystycznie istotna. Cena w sposób istotny wpływa na wielkość popytu.

Zadanie 2

Uzyskano oszacowanie formy liniowej zależności popytu (P) względem dochodów (D) oraz cen (C):

ln P = 0,0107 + 1,2 lnD - 0,3 lnC, R² = 0,981; s= 0,0021,

(14,5) (1,4) (6,7)

a) Model oryginalny ma postać

b) Elastyczność dochodowa popyty wynosi : 1,2

c) elastyczność cenowa : -0,3

d) Gdy dochody wzrosną o 1%, popyt przypuszczalnie wzrośnie o 1,2%, ceteris paribus

e) gdy ceny wzrosną o 1% to popyt przypuszczalnie zmaleje o 0,3%, ceteris paribus

f) Jeśli dochody i ceny wzrosną o 1 % to popyt wzrośnie o około (przybliżenie) 0,9% (1,2 - 0,3)%

g) Model nie jest poprawny, gdyż zmienna D jest statystycznie nieistotna, ponieważ ma empiryczną wartość statystyki t Studenta niższą od 2 (dla większej liczby obserwacji wartości krytyczne t Studenta na poziomie istotności 0,05 wynoszą ponad 2)

Pod parametrami podano empiryczne statystyki t Studenta

Zadanie 3

Przypuszcza się, że wydajność pracy WY (WY = PR/ZA; PR - produkcja, ZA - zatrudnienie) w następujący sposób zależy od technicznego uzbrojenia pracy TUP (TUP = MA/ZA, MA - majątek):

• przy jednostkowym technicznym uzbrojeniu pracy wydajność wynosi 12,3 tys. zł;

• ze wzrostem technicznego uzbrojenia pracy o 1%, wydajność wzrasta o 0,8%.

a) model wydajności względem technicznego uzbrojenia pracy jest : potęgowy

b) a jego wzór ma postać:

c) model produkcji względem zatrudnienia i majątku jest : potęgowy

d) a jego wzór ma postać

e) przy jednostkowych nakładach zatrudnienia i majątku oczekiwana wielkość produkcji wynosi 12,3 tys. zł

f) zbadaj efekt skali produkcji: neutralny, gdyż suma wykładników wynosi 1.

Zadanie 4

Do następujących oszacowań form zlinearyzowanych podaj postać modelu oryginalnego:

1. lnY = 0,65 + 0,03X =>
   

2. Y = 2,34 + 3,45Z (Z=1/X)=>
   

3. lnY = 2,34 + 0,83lnX =>
   

Zadanie 5

Podaj interpretację współczynnika kierunkowego następujących modeli:

4. 
   - jeżeli X wzrośnie o jednostkę, to Y zmaleje o około 4%.

5. 
   - jeżeli X wzrośnie o 1%, to Y spadnie o około 0,04%

6. 
   - jeżeli X wzrośnie o jednostkę, to Y spadnie o około 0,04 jednostki

---