Równ stanu dla sys-ów dynamicznych ciągłych:

Ż(t)=f[ż(t);λ(t);t]

Z(t_o)= Z_o

Z(t) tε[t_o,t]

λ(t)-wymuszenie ma wartość lokalną

SYST DYNAMICZNY LINIOWY

Jest liniowy jeśli:

Z(t_o)= Z'(t_o)+ Z''(t_o)

λ_tot(·)=λ'_tot(·)+λ''_tot(·)

jeśli jest liniowy to każda odpowiedź powinna być osobna

F[Z'(t_o)+ Z''(t_o); λ'_tot+λ''_tot]=

1. F[Z'(t_o); λ'_tot]+F[Z''(t_o); λ''_tot]

2. Ẑ(t_o)=CZ(t_o)

λ_tot=Cλ_tot(t_o) dla każdego C

F[Ẑ(t_o); λ'_tot]=CF[z(t_o); λ''_tot]-zasada superpozycji

gdy syst jest nieliniowy nie można stosować superpozycji

Tw. Odpowiedź systemu dynamicznego liniowego jest sumą odpowiedzi przejściowej i wymuszonej

Dowód: Niech system będzie liniowy to A i B

| Z(t)=Z+O |

| λ_tot(·)=ơ_tot+ λ_tot | =>

F[Z(t); λ_tot]=F[z(t_o); ơ_tot]+F[o; λ_tot]

Jeżeli syst dynamiczny jest:

a)ciągły

b)liniowy

to równanie jego dynamiki i równanie wyjścia mają postać

Ż(t)=AZ(t)+Bu(t)

Y(t)=CZ(t)

Czasami te równ-a mogą przyjąć postać sztywnych gdzie w opisanych syst-ch pewne rozw-a biegną b szybko a inne b wolno (równ przepływu)

Tw (dla syst-ów dynamicznych liniowych ciągłych) Istnieje macierz Ø(t, t_o) zwana macierzą tranzycyjną, która pozwala obliczyć wektor stanu na chwilę t późniejszą niż to, dla stanów przejściowych (tj. gdy u=0 lub u= ơ_tot tzn zerowe wymieszanie)

Z(t)=Ø(t, t_o)z(t_o)

Własności macierzy tranzycyjnej Ø(t,t_o):

1)własności identyczności- jeśli obydwa argumenty tej macierzy są jednakowe to jeśli to macierz jednostkowa

Ø(t', t')=E

E=|1……0|

|01……|

|………|

|0..…..1|

Dowód: Z(t)= Ø(t, t_o)Z(t_o)

t=t_o=>Z(t_o)= Ø(t_o,t_o)Z(t_o)=> Ø(t_o,t_o)=E

2)Własność łańcuchowa- jeżeli macierz tranzycyjna pomnożona przez siebie ale z naprzemiennymi

Ø(t, t')· Ø(t', t_o)= Ø(t, t_o)

Opis=>Ø(t,tⁿ)·Ø(t'',t^n-1)·Ø(t^n-1,t^n-2)· Ø(t^x, t_o)= Ø(t, t_o)

Dowód

Z(t')= Ø(t', t_o)·Z(t_o)

Z(t)= Ø(t, t')·Z(t')

1)Z(t)= Ø(t, t')·Ø(t', t_o)·Z(t_o)

2) Z(t)= Ø(t, t_o)·Z_o (t_o)

3)Własn odwrotności- macierze odwrotną do macierzy Ø(t,t_o) jest Ø(t_o,t)

Ø^-1(t, t_o)= Ø(t_o,t)

Dowód: Ø(t_o,t)- Ø(t,t_o)= Ø(t_o,t_o)=E

4)własność- macierz tradycyjna Ø(t,t_o) spełnia równ

Ø(t, t_o)/∂t=AØ(t, t_o)

Ø(t_o, t_o)=E

Dowód:Z(t)= Ø(t, t_o)Z(t_o)

(1)Z'(t)= ∂Ø(t, t_o)/∂t · Z(t_o)

(2) Z'(t)=AZ(t)=A· Ø(t, t_o)Z(t_o)

=>∂Ø(t, t_o)/∂t · Z(t_o)= A· Ø(t, t_o)Z(t_o)

5)własność- macierz odwrotna do Ø(t, t_o) tj macierz Ø(t_o,t) (dla u=0) spełnia następujący układ równań różniczkowych

∂Ø(t_o,t)/∂t=- Ø(t_o,t)·A

Ø(t_o,t_o)=E

Dowód:E= Ø(t_o,t)· Ø(t,t_o)

0=∂Ø(t_o,t)/∂t·Ø(t,t_o)+ Ø(t_o,t)·∂Ø(t,t_o)/∂t

0=∂Ø(t_o,t)/∂t·Ø(t,t_o)+Ø(t_o,t)·A· Ø(t,t_o)

0=∂Ø(t_o,t)/∂t·Ø(t,t_o)· Ø(t_o,t)+ Ø(t_o,t)·A· Ø(t,t_o)·Ø(t_o,t)

0=∂Ø(t_o,t)/∂t+ Ø(t_o,t)·A

6)Własność- jak wykorzystać macierz tranz

Ø(t,t_o) gdy u(t)≠o (u(t)≠ơ_tot)

∂Ø(t_o,t)/Z(t)=AZ(t)+Bu(t)

Ø(t,t_o)Z(t)+∂Ø(t_o,t)/∂t·Z(t)= Ø(t,t_o) Bu(t)

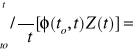
Ø(t,t_o) Bu(t)

Z(t)= Ø(t,t_o) Z(t)+

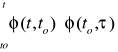
Bu(τ)dτ

Z(t)= Ø(t,t_o) Z(t)+

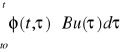
ZBIORNIK LINIOWY

h(t)=he^-k*(t-to)+

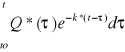
Tw: Ø(t,t_o)=

Funkcję tranzycyjną można wyliczyć z powyższego wzoru

Tw:Jeśli macierz A jest diagonalna to

Ø(t,t_o)=diag(e^λ(t-to),…)

Z(t)=diag(e^λ1(t-to),…., e^λn(t-to))Z(t)+
Bu(τ)dτ

Jeśli macierz A jest diagonalna to rowiązania dla wektora stanu są rozprężone

SYST DYNAM STEROWANY-jest całkowicie sterowany jeżeli dla dowolnego stanu początkowego z_o w chwili t_o oraz stanu końcowego z_k w chwili t_k istnieje przedziałami ciągłe skierowanie u_to,t które doprowadzi system z_o z chwili początkowej do stanu końcowego z_k

Przykładem niesterowalnych systemów dynamicznych jest syst gdzie nie mamy wpływu na sterowalność systemów. Przykładem mogą być 2 zbiorniki

Gruba- Linia naturalnego wypływu wody ze zbiornika

Ugieta- opróżnianie zbiornika

Stosowane nadziałami ciągłę (Bang Bang):

Syst dynamiczny: Z=Az+Bu

Metody kreowania systemem dynamicznym:

1)wskazanie palcem

2)sprawdzenie kryterium sterowania

Ad1)

Z=h(t)

h(t)=h_oe^-k*t+

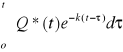
Zał h_o=0 żądamy aby w chwili t_k stan

h_k=0+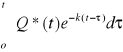

dla zbiornika liniowego stosujemy

szukamy Q*=Q*_o=const

h_k=e^-k*tk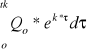

h_ke^-k*tk=Qo^*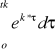

Q_o*=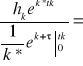

Ad2)

Przedstawi oglny kryterium sterowalności. Tworzy się hipermacierz gdzie na 1 miejscu ustawia się macierz B (dluga)

S=[B|AB|A²B|…|A^n-1B]

Wymiar z=n ilość równań roznickowych

n-ilosc zbiornikow

rank s=n

system dynamiczny jest całkowicie stosowany wtedy i tylko wtedy gdy rzad macierzy S jest rowny wymiarowości wektora stanu

rzad macierzy-ilosc wierszy lub kolumn albo wymiar najwiekseo wyznacznika nie zmniajacego się

przykład syst dynamicznego

Din z=2

z=Az+Bu

vank s=1
n=2

t

t_o t

Z(t)

t_o t

t

Z(t)

t_o t

t

y1

Z1

y2

Z2

y

Z

y1

Z1

y2

Z2

---