Wyznaczanie modułu sztywności metodą dynamiczną Gaussa.

Wyznaczenie modułu sztywności τ metodą Gaussa polega na pomiarze okresów drgań: wibratora nieobciążonego, oraz obciążonego ciałem o prostych kształtach geometrycznych.

Moduł sztywności związany jest z tzw. odkształceniem przesunięcia prostego (ścinanie), które powstaje po przyłożeniu do ciała ścinającej sily stycznej F_t. W skali mikroskopowej odkształcenie przesunięcia prostego tłumaczy się skrzywieniem komórek siatki krystalicznej. Jony zajmują położenia wynikające z równowagi sił działających między nimi. Wskutek działania siły F_t między jonami działają siły, które po zaprzestaniu działania F_t pozwalają komórkom wrócić do położenia równowagi.

Prawo Hook'a - Przyrost długości Δl jakiego doznaje ciało sprężyste rozciągane z siłą F, jest wprost proporcjonalny do wielkości siły i do długości początkowej l0 ciała oraz odwrotnie proporcjonalny do pola przekroju poprzecznego S, a ponadto jest on zależny od rodzaju materiału.

- naprężenie

gdzie: E- moduł Younga (moduł sprężystości podłużnej)

W związku z tym wydłużenie przy rozciąganiu jest wprost proporcjonalne do wartości naprężenia.

Gdzie: P_t - naprężenie styczne, τ - moduł sztywności, ψ - odkształcenie względne

Pod wpływem momentu siły M' pręt ulega skręceniu o pewien kąt ϕ, tzn. dla wybranego elementu dV powierzchnia ds. przesuwa się z położenia A do A' a krawędzie równoległe do BA zajmują położenie równoległe do BA'. DV ulega względnemu przesunięciu
. Ponieważ AA'=ρϕ więc naprężenia styczne
, co odpowiada elementarnemu momentowi sił.

Całkowity moment M' wynosi:

gdzie:
- powierzchniowy moment bezwładności pręta wzg. osi OO'

gdzie:
- moduł skręcenia pręta.

Przy skręceniu pręta o kąt ϕ przyłożeniem zewn. momentu sił M' pojawia się moment wewnętrznych sił M

Jeśli dolny koniec pręta obciążymy ciałem symetrycznym wzg. osi OO' to ruch tego ciała jest opisany zgodnie z II zasadą dynamiki Newtona: „Jeżeli na ciało działa niezrównoważona siła to ciało będzie poruszać się ruchem jednostajnie zmiennym, z przyspieszeniem wprost proporcjonalnym do działającej siły i odwrotnie proporcjonalnie do masy tego ciała.”

gdzie: I moment bezwładności ciała

Równanie to określa ruch drgający prosty o częstości
, a więc okresie

gdzie: T - okres drgań nieobciążonego wahadła, I- moment bezwładności wahadła, D- moment skręcający

Wyznaczenie modułu sztywności τ metodą Gaussa polega na pomiarze okresów drgań: wibratora nieobciążonego, oraz obciążonego ciałem o prostych kształtach geometrycznych (metalowe obręcze). Pojawiającym się problemem jest wyznaczenie momentu bezwładności wibratora. Okres drgań dla wibratora nieobciążonego opisany jest zależnością:

gdzie: T₁ - okres drgań nieobciążonego wahadła, I- moment bezwładności wahadła, D- moment skręcający

dla wibratora obciążonego ciałem o znanym momencie bezwładności I₀:

gdzie: T₂ - okres drgań obciążonego wahadła, I- moment bezwładności wahadła, D- moment skręcający , I₀- moment bezwładności obciążenia

Z powyższych wzorów na okresy drgań wyznaczamy:

a po uwzględnieniu zależności na moduł skręcenia danego pręta:

otrzymujemy:

W laboratorium pomiary wyznaczenia modułu sztywności przeprowadzano dla obręczy metalowych, o przekroju kołowym, dla których powierzchniowy moment bezwładności oznacza się:

Ciałami o prostych kształtach są metalowe obręcze, których moment bezwładności wyraża się wzorem:

gdzie: m - masa obręczy,

D₁, D₂ - średnice: wewnętrzna i zewnętrzna jednej obręczy;

Ostatecznie wzór na moduł sztywności przyjmuje postać:

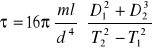
gdzie: τ- moduł sztywności materiału, m- masa obciążenia, l - długość drutu na którym zwieszone jest wahadło, d - promień drutu, D₁-śr. wew. obręczy, D₂-śr. zewn. obręczy,

T₂-okres drgań obciążonego wahadła, T₁ - okres drgań nieobciążonego wahadła.

POMIARY

Do wykonania pomiarów zostały zastosowane dwa wibratory o nieznanych momentach bezwładności I, różnych długościach i średnicach drutów na których były zawieszone. Czego ilustracją jest poniższa tabelka:

	Długość l [cm]	Średnica [cm]	Promień d [cm]	Czas 10 wychyleń [s]
1
2

W celu wyeliminowania nieznanej wartości momentu bezwładności wahadła nieobciążonego, umieszczamy dodatkowe obciążenie o znanej wartości masy i średnicy. Naszym obciążeniem są dwie obręcze o poniższych parametrach:

	Masa [kg]	Promień D1 [mm]	Promień D2 [mm]	Czas 10 wychyleń [s]
1
2

Dokonując pomiaru 10 drgań wahadła jesteśmy w stanie wyznaczyć przy pomocy stopera okres drgań, czego efektem są wyniki zamieszczone poniżej:

	Okres wahadła nieobciążonego T0 [s]	Okres wahadła obciążonego T [s]
1
2

Znając już wszystkie potrzebne dane, jesteśmy w stanie obliczyć poszczególne moduły sztywności dla badanych drutów.

	Moduł sztywności badanego drutu τ [kg/ms^2]	Błąd pomiaru [Δτ/τ]	Moduł sztywność z uwzględnieniem błędu pomiaru
1
2

Ocena niepewności pomiarowych uzyskana pry zastosowania metody różniczki zupełnej.

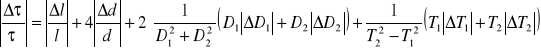
gdzie :

d - jest potrójnym błędem standardowym wartości średniej d,

l , D₁ , ₁ , D₂ , ₂ - są błędami maksymalnymi wartości średnich,

bł*d pomiaru masy ±0,01 kg

bł*d wzgl*dny *ruby mikrometrycznej ±0,01 mm

bł*d wzgl*dny suwmiarki ±0,1 mm

METODYKA OBLICZEŃ:

WNIOSKI:

Z faktów wykazanych za pomocą doświadczenia jak i obliczeń uzyskujemy niepodważalne dowody, iż wartości rzeczywiste są zafałszowane w bardzo małym stopniu, co pozwala na osobiste zadowolenie z metodyki przeprowadzania doświadczenia jak i uzyskanych wyników. Na nieznaczne odchylenia od faktycznego stanu mają wpływ następujące czynniki:

• Wyeksploatowany sprzęt.

• Liczne odkształcenia plastyczne drutu powstałe na skutek nieprawidłowego użytkowanie przez osoby przeprowadzające doświadczenia.

• Nieudolność, a raczej nieprecyzyjność osoby przeprowadzającej doświadczenie charakteryzujące się niezbornością ruchową. Mam tu na myśli nie jednoczesne włączenie przyrządu pomiarowego czasu z momentem rozpoczęcie drgań wahadła zarówno obciążonego jak i nieobciążonego.

• Czynniki zewnętrzne (wszelkiego rodzaje oporu ruchu) powodujące, iż drgania wahadła są nie dokładne, o niejednoznacznym wychyleniu z położnie równowagi.