Dr Maria Jadamus-Hacura
Metody analizy współzależności zjawisk
Rodzaje zale*no*ci wyst*pujących w badaniach społeczno-gospodarczych
Analiza zale*no*ci korelacyjnej
Wsp*łczynnik korelacji liniowej Pearsona
Wyznaczanie parametr*w liniowej funkcji regresji metodą najmniejszych kwadrat*w na podstawie danych szczegółowych
Miary dopasowania modelu do danych empirycznych
1. Rodzaje zale*no*ci wyst*pujących w badaniach społeczno-gospodarczych
Analiza struktury w rozkładzie empirycznym dotyczyła zmienności jednej cechy. W wielu jednak przypadkach zjawisko może być charakteryzowane przez więcej niż jedną cechę. Cechy tego mogą być ze sobą powiązane i wówczas pojawia się potrzeba łącznego ich badania. Badanie to ma na celu ustalenie w jaki sposób i jak silnie powiązane są ze sobą rozpatrywane cechy. Na gruncie metod ilościowych problematyka ta należy do zagadnień związanych z teorią współzależności.
Rodzaje zależności:
Funkcyjna - charakteryzuje się wzajemnym, jednoznacznym przyporządkowaniem wartości dwóch cech. Każdej wartości cechy X odpowiada dokładnie jedna wartość cechyY. Zależność ta nie występuje w przypadku zjawisk gospodarczych.
Stochastyczna
Zależność stochastyczna występuje wtedy gdy wraz ze zmianą wartości jednej zmiennej zmienia się rozkład prawdopodobieństwa drugiej zmiennej.
Korelacyjna (statystyczna)
Związek korelacyjny polega na tym, że określonym wartościom jednej zmiennej odpowiadają ściśle określone średnie wartości drugiej zmiennej. Można zatem obliczyć, jak zmieni się - średnio biorąc - wartość zmiennej zależnej Y w zależności od wartości zmiennej niezależnej X. Oczywiście najpierw na podstawie analizy merytorycznej należy uzasadnić logiczne występowanie związku, a dopiero potem przystąpić do określenia siły i kierunku zależności. Zwróćmy uwagę, że liczbowe stwierdzenie występowania współzależności nie zawsze oznacza występowanie związku przyczynowo-skutkowego między badanymi zmiennymi. Współwystępowanie dwóch zjawisk może również wynikać z bezpośredniego oddziaływania na nie jeszcze jednego, trzeciego już zjawiska. Zależność korelacyjna jest szczególnym przypadkiem zależności stochastycznej.
2. Analiza zale*no*ci korelacyjnej
Prostym sposobem wykrywania związku korelacyjnego między badanymi cechami jest obserwacja szeregów statystycznych, które zawierają informację o tych cechach.
Wykresy, które reprezentują obrazowo związek pomiędzy zmiennymi, nazywane są wykresami rozrzutu (catterplot). Analizę zależności powinno się rozpoczynać od ich sporządzenia. Wzrokowa ocena umożliwia często określenie siły i rodzaju zależności.
Przyjmijmy, że zbiorowość jest badana ze względu na dwie zmienne X i Y, a realizacje tych zmiennych w populacji lub próbie n-elementowej zestawione są w postaci dwóch szeregów szczegółowych lub rozdzielczych. W prostokątnym układzie współrzędnych na osi odciętych zaznaczamy zmienną niezależną a na osi rzędnych wartości zmiennej zależnej. Punkty, odpowiadające poszczególnym wartościom cech, tworzą korelacyjny wykres rozrzutu. . Jeżeli punkty układają się w nieregularną chmurę, to nie ma żadnego związku między zmiennymi. Jeżeli natomiast punkty układają się wzdłuż prostej lub pewnej krzywej, to można doszukiwać się takiego związku. Poszukiwaniem takich związków zajmuje się analiza regresji.
Korelacja dodatnia występuje wtedy, gdy wzrostowi wartości jednej cechy odpowiada wzrost średnich wartości drugiej cechy.
Korelacja ujemna występuje wtedy, gdy wzrostowi wartości jednej cechy odpowiada spadek średnich wartości drugiej cechy.
Natężenie (siłę) współzależności dwóch zmiennych można wyrazić liczbowo za pomocą wielu mierników. Najbardziej popularny jest współczynnik korelacji liniowej Pearsona.
Współczynnik ten (oznaczony symbolem rxy i przyjmujący wartości z przedziału [-1,1]) jest miernikiem siły związku prostoliniowego między dwiema cechami mierzalnymi.
Wzór na współczynnik korelacji liniowej Pearsona jest następujący:
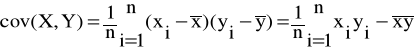
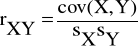
gdzie:
Własności współczynnika korelacji Pearsona:
wartości w zakresie -1 Ⴃ rxy Ⴃ 1,
symetryczność: rxy = ryx,
wskazuje kierunek korelacji
gdy: |r|<0.3 - korelacja niewyraźna
0,3 Ⴃ |r|Ⴃ 0,5 - korelacja wyraźna
0,5 Ⴃ |r|Ⴃ 0,7 - korelacja silna
0,7 Ⴃ |r|< 1,0 - korelacja bardzo silna
Znak współczynnika korelacji informuje nas o kierunku korelacji, natomiast jego bezwzględna wartość - o sile związku. Mamy oczywiście równość rxy = ryx. Gdy rxy =|1|, to zależność korelacyjna przechodzi w zależność funkcyjną (funkcja liniowa). Jeśli natomiast rxy = 0, oznacza to zupełny brak związku korelacyjnego między badanymi zmiennymi X i Y. Wykresy rozrzutu dla różnych wartości współczynnika korelacji pomiędzy zmiennymi X i Y przedstawiono w arkuszu programu Excel : „Wykresy rozrzutu”.
3. Wyznaczanie parametr*w liniowej funkcji regresji metodą najmniejszych kwadrat*w na podstawie danych szczegółowych
Klasyczna metoda najmniejszych kwadratów ( NMK ) polega na takim oszacowaniu parametrów funkcji regresji, aby dla danych z próby wyrażenie
= [yi - f(xi) ]2
osiągnęło minimum.
W przypadku funkcji regresji liniowej:
![]()
= ax+b (1)
otrzymujemy:
= [yi -axi -b)2 → min.
Obliczając pochodne cząstkowe funkcji Ψ względem a i b otrzymujemy tzw. układ równań normalnych:
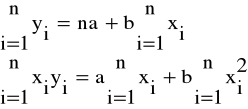
z którego wyznaczamy wartości parametrów a i b funkcji regresji liniowej:
![]()
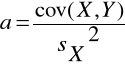
3. Miary dopasowania modelu do danych empirycznych
Odchylenie standardowe składnika resztowego
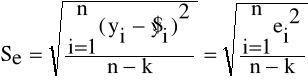
gdzie:
n - liczebność próby
k - liczba szacowanych parametrów
ei - składniki resztowe (reszty)
![]()
Empiryczny współczynnik zbieżności i współczynnik determinacji
Wiadomo, że jeżeli oszacujemy model regresji liniowej postaci (1) klasyczną metodą najmniejszych kwadratów, to zachodzi równość: suma kwadratów odchyleń zmiennej objaśnianej od jej wartości średniej (czyli zmienność zmiennej zależnej) jest sumą zmienności wyjaśnionej regresją i zmienności resztowej, co możemy zapisać w postaci równania:
(yi - ![]()
)2 = (![]()
- ![]()
)2 + (yi - ![]()
)2
Po podzieleniu powyższego równania przez wyrażenie występujące po lewej stronie otrzymujemy:
![]()
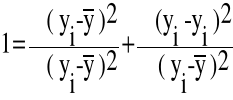
Składniki po prawej stronie oznaczamy następująco:
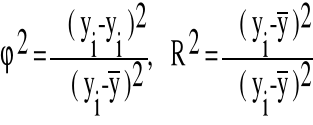
Przykład badania zależności pomiędzy dochodami, a wydatkami wybranej próbie gospodarstw domowych przedstawiono w pliku programu Excel „ Funkcja regresji”
6
Wartość współczynnika determinacji R2 zawiera się w przedziale <0,1> i informuje jaka część zaobserwowanej w próbie całkowitej zmienności y została wyjaśniona regresją liniową względem x .
Współczynnik zbieżności 2 zawiera się w przedziale <0,1> i informuje jaka część zaobserwowanej w próbie całkowitej zmienności y jest dziełem przypadku ( nie została wyjaśniona regresją liniową względem x ).
![]()
Wielkość odchylenia standardowego reszt interpretujemy jako przeciętne odchylenie zaobserwowanych wartości zmiennej zależnej yi od jej wartości teoretycznych.
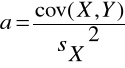
Wartość współczynnika regresji - a wyraża, o ile przeciętnie (średnio) zmieni się (wzrośnie lub zmniejszy się ) zmienna y, jeśli zmienna niezależna x wzrośnie o jednostkę.
Równanie regresji jest ilościowym wyrazem zależności między określonymi wartościami zmiennej niezależnej X i odpowiadającymi im średnimi wartościami zmiennej zależnej Y:
![]()
gdzie:
![]()
- nieznana warunkowa średnia wartość zmiennej zależnej
x - określona (znana) wartość zmiennej niezależnej
f - określona postać funkcji

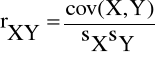
Zawartość modułu: