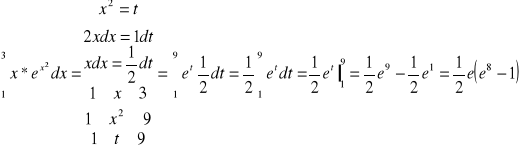
Badanie przebiegu zmienności funkcji
Wyznaczenie dziedziny (wykluczenie punktów z dziedziny w wypadku: mianownika; pierwiastka; funkcji logarytmicznej (podstawa dodatnia); funkcji x2 itp.)
miejsca zerowe
Granice na przedziałach oznaczoności (granice prawostronne i lewostronne dla punktów wykluczonych z dziedziny)
Pierwsza pochodna
Druga pochodna
Asymptoty
Wnioski z pochodnych
Monotoniczność (tam, gdzie f ` >0 rosnąca, f ` <0 malejąca, f'=0 stała; czyli wyznaczamy tam, gdzie zero i patrzymy po której są wartości dodatnie, a po której ujemne)
Pierwsza pochodna (tam, gdzie f ` =0 punkty podejrzewane - warunek konieczny; gdzie przy f ` =0 i f ' ' </>0 to maksimum/minimum)
Druga pochodna (tam, gdzie f ` ` = 0 punkty podejrzewane; sprawdzamy licząc granicę lewostronną i prawostronną punktu podejrzewanego o istnienie przegięcia i sprawdzamy, czy znak się zmienia)
Tabelka
Szkic wykresu
Zmiana granic całek oznaczonych.
Przykład z wykładu:
Metoda 1.
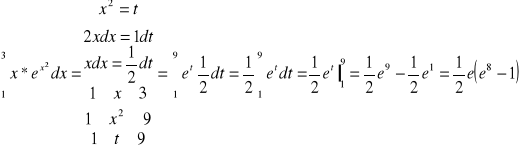
Metoda 2. Obliczamy najpierw całkę nieoznaczoną (podstawienie itp.) następnie z wynik przepisujemy i obliczamy z normalnymi granicami (tu 1 i 3).