Zestaw z1

1. Badając kosztochłonność produkcji pewnego detalu wyznaczono na podstawie 25 elementowej próby następujący przedział ufności dla średniej generalnej:

Średnia arytmetyczna wyznaczona z tej próby jest równa: ..
.......................

Proszę uzasadnić odpowiedź .
.

2. Jaką decyzję można podjąć odnośnie prawdziwości hipotezy zakładającej, że średnia kosztochłonność jest równa 1,13 zł na podstawie przedziału ufności z zadania 1:

a) odrzucamy H0 b) nie odrzucamy H0 c) nie wiadomo d) przyjmujemy H0

Proszę uzasadnić odpowiedź ...
.

3. Warunkiem koniecznym do zweryfikowania hipotezy o równości dwóch średnich generalnych jest:

a) równość wariancji b) równość średnich c) nierówność wariancji d) nierówność średnich

4. Jeżeli zwiększymy liczebność próby, to rozpiętość przedziału ufności dla średniej:

a) zmniejszy się b) zwiększy się c) nie zmieni się d) nie wiadomo

Proszę uzasadnić odpowiedź ..przy wzroście n maleje .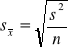

5. Jaką decyzję można podjąć odnośnie równoważności dwóch różnych systemów produkcyjnych, jeżeli na podstawie prób losowych ustalono, że najmniejsza istotna różnica jest równa 0,25 a różnica średnich 0,24:

a) odrzucamy H0 b) nie odrzucamy H0 c) nie wiadomo d) przyjmujemy H0

Proszę uzasadnić odpowiedź ..

6. Porównując wpływ dwóch różnych systemów organizacji pracy na dzienną wydajność produkcji pewnego detalu (na 1 zatrudnionego) uzyskano w pierwszym systemie średnio 15 szt/dzień, a w drugim odpowiednio 16,8 szt/dzień. Wiedząc, że błąd różnicy średnich wyznaczony łącznie na podstawie 20 obserwacji jest równy 0,6 szt/dzień zweryfikuj, na 95% poziomie ufności przypuszczenie, że średnie wydajności w obu systemach są takie same wobec alternatywy, że w pierwszym systemie uzyskujemy istotnie mniejszą wydajność

z zadania mamy:

stąd

z tablic mamy
1,73

Ponieważ
to H₀ odrzucamy na korzyść H₁

7. Weryfikując hipotezę w zadaniu 6 możemy spotkać się z taką sytuacją, że nie odrzucimy hipotezy faktycznie fałszywej. Jak się nazywa błąd tego rodzaju i jaką mamy szansę jego popełnienia.

Odp. Jest to błąd II rodzaju, a jego p-stwo oznaczamy jako

8. Test
Pearsona znajduje zastosowanie między innymi w zagadnieniach:

1. badania zgodności rozkładów danej cechy w kilku populacjach

2. zgodności rozkładu empirycznego z rozkładem normalnym przy małej próbie (n < 50)

3. analizy wariancji

4. szczegółowych porównaniach średnich

9. Wartość empiryczna statystyki Chi-kwadrat dla zweryfikowania hipotezy o zgodności ocen ze statystyki (skala: 2, 3, 3+, 4, 4+ i 5) w trzech grupach studenckich jest równa 4,56. Na 95% poziomie ufności pozwala to na:

a) odrzucenie H0 b) nie odrzucenie H0 c) nie wiadomo d) przyjęcie H0

Proszę uzasadnić odpowiedź : ponieważ
....

Zestaw Z2

1. Badając kosztochłonność produkcji pewnego detalu wyznaczono na podstawie 25 elementowej próby następujący przedział ufności dla średniej generalnej:

Średnia arytmetyczna wyznaczona z tej próby jest równa: ..
.

Proszę uzasadnić odpowiedź

2. Jaką decyzję można podjąć odnośnie prawdziwości hipotezy zakładającej, że średnia kosztochłonność jest równa 11,13 zł na podstawie przedziału ufności z zadania 1:

a) odrzucamy H0 b) nie odrzucamy H0 c) nie wiadomo d) przyjmujemy H0

Proszę uzasadnić odpowiedź .
.

3. Warunkiem koniecznym do zweryfikowania hipotezy o równości dwóch średnich generalnych jest:

a) równość wariancji b) równość średnich c) nierówność wariancji d) nierówność średnich

4. Jeżeli zmniejszymy liczebność próby, to rozpiętość przedziału ufności dla średniej:

a) zmniejszy się b) zwiększy się c) nie zmieni się d) nie wiadomo

Proszę uzasadnić odpowiedź . przy zmniejszeniu n wzrośnie .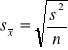

5. Jaką decyzję można podjąć odnośnie równoważności dwóch różnych systemów produkcyjnych, jeżeli na podstawie prób losowych ustalono, że najmniejsza istotna różnica jest równa 0,25 a różnica średnich 0,26:

a) odrzucamy H0 b) nie odrzucamy H0 c) nie wiadomo d) przyjmujemy H0

Proszę uzasadnić odpowiedź .
.

6. Porównując wpływ dwóch różnych systemów organizacji pracy na dzienną wydajność produkcji pewnego detalu (na 1 zatrudnionego) uzyskano w pierwszym systemie średnio 16,8 szt/dzień, a w drugim odpowiednio 15,0 szt/dzień. Wiedząc, że błąd różnicy średnich wyznaczony łącznie na podstawie 20 obserwacji jest równy 0,6 szt/dzień zweryfikuj, na 95% poziomie ufności przypuszczenie, że średnie wydajności w obu systemach są takie same wobec alternatywy, że w pierwszym systemie uzyskujemy istotnie większą wydajność

z zadania mamy:

stąd

z tablic mamy
1,73

Ponieważ
to H₀ odrzucamy na korzyść H₁

7. Weryfikując hipotezę w zadaniu 6 możemy spotkać się z taką sytuacją, że odrzucimy hipotezę faktycznie prawdziwą. Jak się nazywa błąd tego rodzaju i jaką mamy szansę jego popełnienia.

Odp. Jest to błąd I rodzaju, a szansa jego popełnienia to

8. Test
Pearsona znajduje zastosowanie między innymi w zagadnieniach:

1. badania zgodności rozkładów danej cechy w kilku populacjach

2. zgodności rozkładu empirycznego z rozkładem normalnym przy małej próbie (50<n < 100)

3. analizy wariancji

4. szczegółowych porównaniach średnich

9. Wartość empiryczna statystyki Chi-kwadrat dla zweryfikowania hipotezy o zgodności ocen ze statystyki (skala: 2, 3, 3+, 4, 4+ i 5) w trzech grupach studenckich jest równa 14,56. Na 95% poziomie ufności pozwala to na:

a) odrzucenie H0 b) nie odrzucenie H0 c) nie wiadomo d) przyjęcie H0

Proszę uzasadnić odpowiedź ..