11.02.2009
Elżbieta Łopuszyńska
155255
Kierunek: ZIP
Test t-Studenta
Test t-Studenta jest testem statystycznym wykorzystywanym do weryfikacji hipotezy o braku różnic pomiędzy dwoma średnimi wartościami analizowanej zmiennej. Test t-Studenta można wykorzystać do porównania różnic pomiędzy średnimi:
w dwóch próbach niezależnych; mogą to być przykładowo dwie losowo wybrane grupy, z których jedną poddano działaniu określonego bodźca, a druga pełni funkcję kontrolną - przy czym należy założyć, że wariancje w grupach są równe.
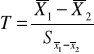
H0:μ1=μ2
Statystyka T ma rozkład t-Studenta
Liczba stopni swobody n1+n2-2
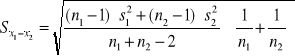
gdzie:
jeżeli |T|< nie ma podstaw do odrzucenia hipotezy zerowej
jeżeli |T|≥ hipoteza zerowa jest odrzucona
w dwóch próbach zależnych, czyli grupie tych samych osób, w których dwukrotnie przeprowadzono określone badanie/pomiar (np. przed i po posiłku)
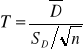
H0:μ1=μ2
Statystyka T ma rozkład t-Studenta
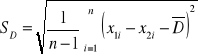
Liczba stopni swobody n1-1
![]()
gdzie:
jeżeli |T|< nie ma podstaw do odrzucenia hipotezy zerowej
jeżeli |T|≥ hipoteza zerowa jest odrzucona
w próbie pojedynczej; w tym wypadku średnia obserwowana w próbie jest porównywana ze średnią oczekiwaną w całej populacji, z której próba została pobrana.
Po oszacowaniu modelu wyłania się potrzeba sprawdzenia hipotez o jego parametrach. Jeśli bowiem hipoteza głosząca, iż parametr jest nieistotny jest prawdziwa oznacza to brak wpływu zmiennej objaśniającej na zmienną endogeniczną.
![]()
W badaniu istotności parametrów wyróżnia się dwa podstawowe testy służące do sprawdzenia istotności parametrów. Pierwszy z nich zakłada, że wszystkie parametry strukturalne modelu, poza wyrazem wolnym są równe zero. Hipoteza Ho ( ) zakłada więc, że wszystkie zmienne objaśniające nie oddziałują na zmienną endogeniczną, co oznacza, iż nie powinny się znaleźć w modelu. Sprawdzianem tej hipotezy jest statystyka:
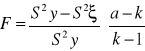
Gdzie
oznacza całkowitą, zaobserwowaną w próbie wariancję zmiennej endogenicznej, która równa się sumie kwadratów odchyleń dzielonych przez n - k.
W badaniu istotności parametrów możliwe jest także inne podejście. Zakłada ono osobne badanie poszczególnych parametrów. Badanie istotności w tym przypadku sprowadza się do weryfikacji hipotez:
Ho: i = 0
Czyli hipoteza, że i-ta zmienna nie wpływa w istotny sposób na zmienną endogeniczną. Hipoteza alternatywna jest sformułowana następująco:
H1: i
0
Sprawdzianem testu jest statystyka Studenta o n - k stopniach swobody wyznaczana jako:
![]()
gdzie:
ai - ocena i-tego parametru,
αi - prawdziwa wartość parametru (zgodnie z hipotezą zerową i=0),
D(ai) - błąd średni szacunku parametru.
Jednostronny a dwustronny test t-studenta. Jeżeli jest to możliwe i istnieją takie przesłanki, to należy zastosować test jednostronny. W teście jednostronnym porównujemy wartość t z fraktylem ![]()
. W teście dwustronnym porównuje się ![]()
z ![]()
![]()
![]()
Test t-Studenta pozwala udowodnić istnienie różnic między grupami. W celu udowodnienia braku tych różnic chciałoby się w teście dwustronnym zamienić role hipotezy zerowej i alternatywnej:
i
Moc takiego testu była by równa 0.
Test t-Studenta w porównaniu z innymi testami statystycznymi ma więcej wymagań, jest za to silniejszy i bardziej pożądany. Pierwszym warunkiem jest założenie, że pomiary podlegają rozkładowi normalnemu. Dlatego właśnie konieczne jest sprawdzenie rozkładu zmiennej w analizie częstości. Drugim założeniem testu Studenta jest założenie o równości wariancji (dwie porównywane grupy powinny być podobnie homogeniczne).
Rozkład t-studenta jest bardziej precyzyjną wersją rozkładu normalnego. Rozkład t-studenta charakteryzowany jest dodatkowo przez tzw. liczbę stopni swobody. Oznacza to, że rozkład ten (posiadając stałą średnią i odchylenie standardowe) jest bardziej spłaszczony dla niewielkiej liczby stopni swobody, zaś gdy liczba ta przekracza 120 i dąży do nieskończoności, rozkład t-studenta upodabnia się do rozkładu normalnego. Przy niewielkich df wartości krytyczne rozkładu t- studenta są, więc nieco wyższe niż dla rozkładu normalnego. Stąd oszacowany przedział ufności dla średniej będzie nieco szerszy, co przestaje dziwić, jeżeli uświadomimy sobie, że uwzględnia on błąd pochodzący z dwóch źródeł, oszacowania średniej i oszacowania odchylenia standardowego.
![]()
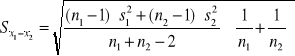
![]()
![]()
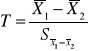
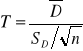
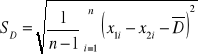
![]()
Wyszukiwarka