RACHUNEK RÓŻNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ CZ.3
Twierdzenia o wartości średniej.
Poniższe trzy twierdzenia zwane są twierdzeniami o wartości średniej.
Twierdzenie 1. (ROLLE'A)
Jeżeli funkcja f jest ciągła w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:56:00 2001
], różniczkowalna w przedziale [Author ID0: at Tue Aug 14 14:57:00 2001
][Author ID0: at Tue Aug 14 14:57:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:57:00 2001
] oraz [Author ID0: at Tue Aug 14 14:58:00 2001
][Author ID0: at Tue Aug 14 14:58:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:58:00 2001
], to istnieje przynajmniej jeden punkt [Author ID0: at Tue Aug 14 14:59:00 2001
][Author ID0: at Tue Aug 14 14:59:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:59:00 2001
] taki, że
![]()
.
Twierdzenie 2. (CAUCHY'EGO )
Jeżeli funkcje ![]()
i ![]()
są ciągłe w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:56:00 2001
], różniczkowalne w przedziale [Author ID0: at Tue Aug 14 14:57:00 2001
][Author ID0: at Tue Aug 14 14:57:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:57:00 2001
] to istnieje przynajmniej jeden punkt [Author ID0: at Tue Aug 14 14:59:00 2001
][Author ID0: at Tue Aug 14 14:59:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:59:00 2001
] taki, że
![]()
.
Twierdzenie 3. (LAGRANGE'A).
Jeżeli funkcja f jest ciągła w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001
][Author ID0: at Tue Aug 14 14:56:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:56:00 2001
]i różniczkowalna w przedziale [Author ID0: at Tue Aug 14 14:57:00 2001
][Author ID0: at Tue Aug 14 14:57:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:57:00 2001
], to istnieje punkt [Author ID0: at Tue Aug 14 14:59:00 2001
][Author ID0: at Tue Aug 14 14:59:00 2001
]![]()
[Author ID0: at Tue Aug 14 14:59:00 2001
] taki, że
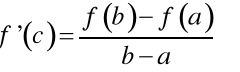
.
Szeregi Taylora i Maclaurina
Definicja 1.
Niech funkcja ![]()
ma w punkcie ![]()
pochodne dowolnego rzędu.
Szereg potęgowy
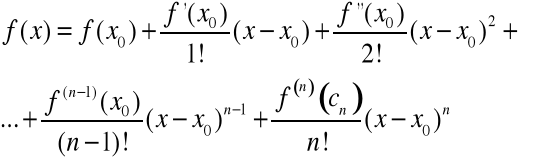
nazywamy szeregiem Taylora funkcji ![]()
o środku w punkcie ![]()
.
Ostatni składnik sumy występującej w powyższym wzorze oznaczać będziemy jako ![]()
i nazywać resztą w postaci Lagrange'a. Tak więc
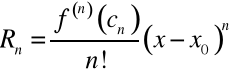
Wniosek. Dla ![]()
otrzymujemy twierdzenie Lagrange'a.
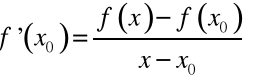
Jeżeli ![]()
, to szereg ten nazywamy szeregiem Maclaurina funkcji ![]()
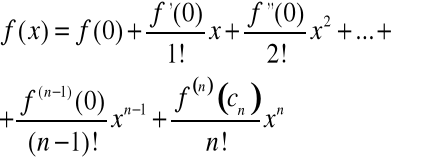
Twierdzenie 4. (o rozwijaniu funkcji w szereg Taylora).
Jeżeli:
funkcja

ma w otoczeniu
pochodne dowolnego rzędu,
dla każdego
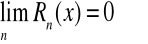
,
to
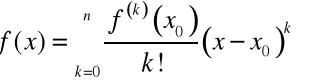
, ![]()
.
Twierdzenie 5. (O jednoznaczności rozwinięcia funkcji w szereg potęgowy)
Jeżeli
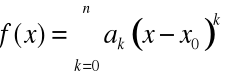
, ![]()
.
to
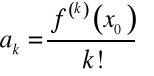
dla ![]()
.
Wzór Taylora oraz wynikający z niego wzór Maclaurina, o których była mowa wykorzystuje się do obliczania przybliżonych wartości funkcji.
Ze wzorów tych możemy otrzymać przybliżenia z mniejszym błędem niż wykorzystując różniczkę pierwszego rzędu.
Zauważmy, że pomijając resztę we wzorze np. Maclaurina, otrzymamy wzór przybliżony
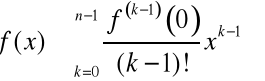
,
który możemy wykorzystać do obliczania wartości funkcji f.
Błąd bezwzględny ![]()
, jaki popełniamy posługując się tym wzorem, jest równy wartości bezwzględnej
reszty ![]()
, tj.
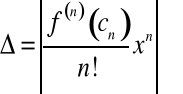
Przykłady
Napisać wzór Maclaurina dla funkcji
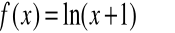
i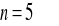
Policzmy:
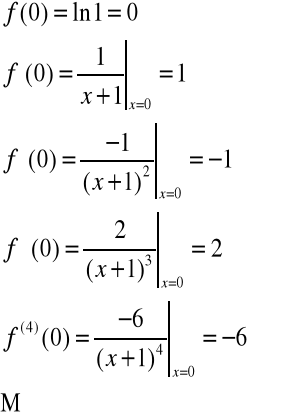
Zapiszemy teraz wzór Maclaurina:
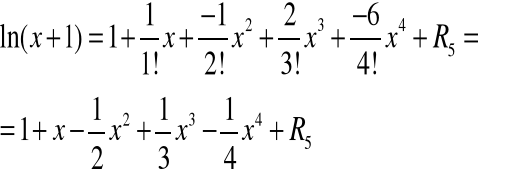
2. Oblicz korzystając z powyższego przybliżenia ![]()
.
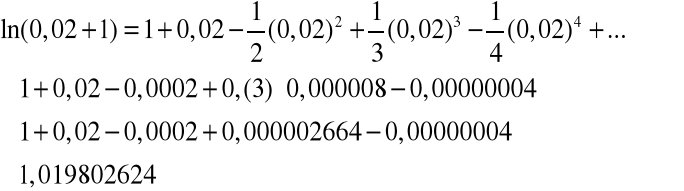
Przypomnijmy, że licząc przybliżoną wartość ![]()
za pomocą różniczki funkcji jednej zmiennej otrzymaliśmy mniej dokładny wynik 1,02.
Twierdzenie 6.
Niech ![]()
, ![]()
będą funkcjami różniczkowalnymi na przedziale I oraz niech ![]()
. Jeżeli ![]()
oraz ![]()
, to ![]()
.
Twierdzenie 7. (REGUŁA DE L'HOSPITALA)
Niech ![]()
i ![]()
będą funkcjami różniczkowalnymi w pewnym sąsiedztwie ![]()
oraz
![]()
.
Jeżeli ![]()
lub ![]()
oraz istnieje granica 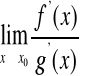
(właściwa lub nie),
to istnieje również granica 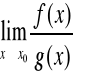
przy czym
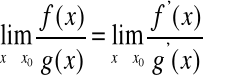
.
Uwaga. Twierdzenie odwrotne nie jest prawdziwe.
Z reguły de l'Hospitala możemy skorzystać w następujących przypadkach:
Przypadek 1.
Niech ![]()
i ![]()
lub niech ![]()
i ![]()
.
Obliczanie granicy poprzez formalne podstawienie wartości granicznych daje nam symbol nieoznaczony ![]()
lub odpowiednio 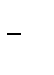
.
W tym przypadku bezpośrednie (być może wielokrotne) zastosowanie reguły de l'Hospitala doprowadzi nas do rozwiązania.
Np.
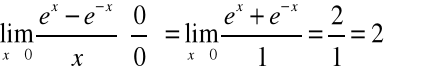
.
Przypadek 2.
Niech ![]()
i ![]()
.
Obliczając granicę 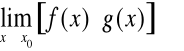
poprzez formalne postawienie wartości granicznych otrzymamy symbol nieoznaczony
![]()
.
Aby wyznaczyć tę granicę zauważmy, że
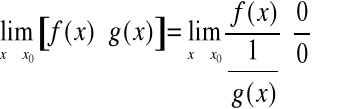
lub
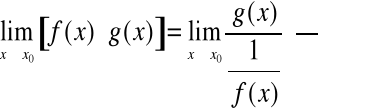
Np.
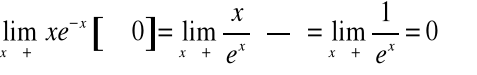
.
Przypadek 3.
Niech ![]()
i ![]()
.
Obliczając granicę 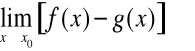
poprzez formalne postawienie wartości granicznych otrzymamy symbol nieoznaczony
![]()
.
Zauważmy, że wówczas mamy:
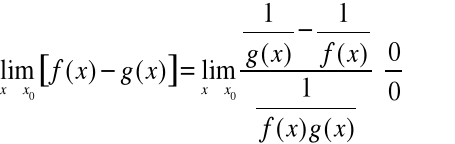
Np. 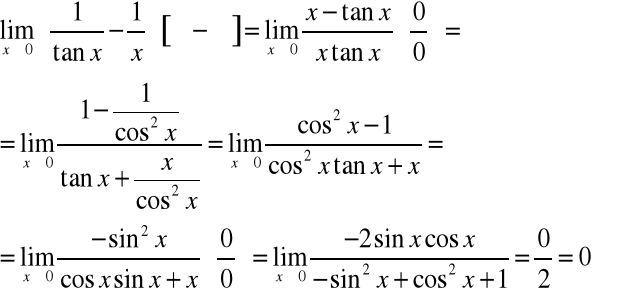
Przypadek 4.
Niech ![]()
i ![]()
.
Obliczając granicę 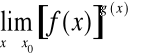
poprzez formalne postawienie wartości granicznych otrzymamy symbol nieoznaczony
![]()
.
Podobnie gdy ![]()
i ![]()
obliczając
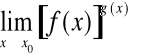
otrzymujemy inny symbol nieoznaczony
![]()
.
Również gdy ![]()
i ![]()
obliczając 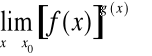
otrzymujemy inny symbol nieoznaczony
![]()
.
We wszystkich tych przypadkach ![]()
, ![]()
, ![]()
obliczenie 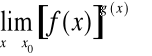
sprowadza się do obliczenia ![]()
, co daje symbol ![]()
.
Np.
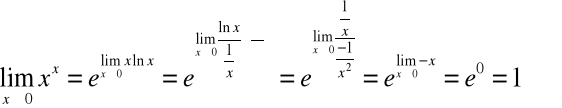
Wyszukiwarka