Wykład 21.

Oligopol oferentów: ustalenie ceny przy heterogenicznej konkurencji.

W konkurencji homogenicznej zakładaliśmy, że produkty wytwarzane przez kilku producentów są nierozróżnialne dla nabywców, czyli nie mają oni żadnych preferencji w stosunku do oferentów. Teraz będziemy rozpatrywać przypadek, gdy nabywcy rozróżniają wyroby poszczególnych producentów i są gotowi płacić różne ceny za te wyroby, które są w stosunku do siebie blisko substytucyjne.

1. Załamana krzywa cena-zbyt

Przyjmuimy, że funkcja cena zbyt na produkt wytwarzany przez jednego z oligopolistów byłaby malejącą prostą przedstawiona na poniższym rysunku jako prosta AB. Przyjmijmy, że ten producent znajduje się w punkcie C, który zapewnia mu osiągnięcie maksymalnego zysku dla jego funkcji kosztów. Tak wyglądałaby funkcja cena-zbyt, pod warunkiem, że na zmiany wielkości produkcji i ceny inni producenci nie reagowaliby zmianami swojej wielkości produkcji i ceny.

Jeżeli będąc w punkcie C zaczołby podnosić cenę na swój wyrób i redukować wielkość produkcji, to jest całkiem prawdopodobne, ze konkurenci nie zareagowaliby na to zmianami cen swoich produktów, czyli odcinek AC okazałby się w warunkach oligopolu realny. Co innego, gdyby zaczoł obniżać cenę na swój wyrób i zwiększać produkcję. W warunkach oligopolu heterogenicznego należy przyjąć, że konkurenci zareagowaliby na takie działania obniżkami cen swoich wyrobów. Wtedy odcinek CB byłby już nieosiągalny. Należy się spodziewać, iż taki sam jak poprzednio spadek ceny wywołby mniejszy wzrost popytu. Czyli, w najprosztszym do prezentacji przypadku, od punktu C obowaiązywałaby prosta CD a nie CB.

Jeżeli funkcja cena-zbyt danego oferenta jest łamaną prostą ACD, to wtedy przychód krańcowy tego producenta będzie nieciągły dla wielkości produkcji odpowiadającej punktowi C. Jeżeli funkcja kosztów krańcowych przechodzi przez obszar nieoznaczony przychodu krańcowego E', to wtedy nie możemy odwołać się do warunku koniecznego na maksimum zysku w postaci: Z - max E' = K_c'. Przyjmijmy, że maksimum zysku ten producent osiągał dla kosztów krańcowych K_c1', gdy p i y odpowiadały punktowi C. Z rysunku 1 wynika, że gdyby koszty produkcji tego oferenta spadły, czyli nowa funkcja kosztów krańcowych przebiegałaby jak K_c2', to wtedy optymalna wielkość produkcji nie uległaby zmianie. Takie zjawisko, polegające na tym, że oligopoliści dążący do maksymalizacji zysku nie zwiększają produkcji i nie obniżają cen na swój wyrób mimo występujacej obnizki kosztów produkcji nazywa się najczęściej skostnieniem cenowym na rynku oligopolistycznym. Bez przyjęcia dodatkowych założeń dotyczących sposobu zachowań innych oligopolistów, przbiegu ich funkcji kosztów nie można ustalić dokładnie jaki stan równowagi ukształtuje się na tym rynku. Opisany wyżej przypadek należy potraktować jako przyczynek. Pełniejsza analiza będzie przedstawiona w następnym punkcie.

2. Heterogeniczny duopol cenowy.

Poszerzone rozwiązanie Cournota i von Stackelberga.

Z poprzednich modeli Cournota i Stackelberga obowiązują nadal założenie, że

Dla uproszczenia analizy przyjmijmy następujące założenia:

1. Na rynku istniej tylko dwóch producentów, którzy zachowują się autonomicznie.

2. Nabywcy rozróżniają produkty wytwarzane przez tych dwóch producentów i w związku z tym występują preferencje cenowe ze strony nabywców.

3. Funkcje cena zbyt obu oferentów określają wzory 1 i 2:

(1)

(2)

gdzie:

Wielkości produkcji, które oligopolista może sprzedać na rynku po ustaleniu ceny na swój wyrób zależy również od ceny ustalonej przez konkurenta. Funkcje cen-zbyt danego oferenta dla określonej ceny konkurenta są typowo nachylonymi prostymi. Jeżeli w równaniu 1 przyjmiemy, że p₂ jest dane, to widać, że wzrost p₁ będzie powodował spadek y₁ i odwrotnie spadek p₁ prowadzi do wzrostu y₁. Jest to więc typowa zależność.

Aby zrozumieć ekonomiczny sens ograniczenia należy wyprowadzić wzór na zagregowaną funkcję cena-zbyt. Będzie ona określona wzorem:

(3)

Widać teraz, że tylko wtedy gdy , wzrost ceny p₁ będzie prowadził do spadku zagregowanej podaży, przy niezmienionej cenie p₂. Jeżeli natomiast , to wzrost ceny p₂ przy stałej p₁ będzie powodował ogólny spadek podaży. Takie zależności uznaje się za typowe, dlatego zostały przyjęte w założeniu 3.

Zobaczmy jak będą wyglądały funkcje cena-zbyt 1 producenta wyznaczone dla przykładowych wielkości ceny p₂. W tym celu przekształcamy odpowiedni wzór 1. Otrzymujemy wtedy:

(4)

Łatwo ustalić, że dla różnych p₂ będą one przebiegać równolegle w stosunku do siebie. Narysujmy najpierw trzy przypadki dla cen p₂ odpowiadających kolejno 0, 10, 20. Przedstawia to rysunek 1. Cena p₂ nie może być jednak dowolnie duża, gdyż y₂ musi być większe lub równe 0. Maksymalną wielkość p₂, przy której y₂ = 0 (czyli na rynku pozostałby wtedy tylko 1 producent) możemy ustalić wstawiając do równania 2 y₂ = 0. Otrzymamy wtedy:

(5)

Jeżeli tą maksymalną wielkość p₂ wstawimy ponownie do funkcji cena-zbyt 1 producenta czyli do wzoru 4, to otrzymamy po przekształceniach:

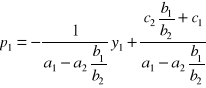
(6)

Jeżeli porównany wskaźniki kierunkowe prostej ze wzoru 6 z prostą z wzoru 4, to stwierdzimy, że prosta ze wzoru 6 musi być ujemnie nachylona i bardziej stroma niż ze wzoru 4, gdyż z założenia 3 wiemy, że:
. Oznacza, to że prosta cena-zbyt określona dla maksymalnej ceny p_2max musi być bardziej stroma niż proste cena-zbyt określone dla ceny p₂ równej 0, 10 bądź 20.

Jeżeli teraz wykreślimy izolinie zysku identycznie jak to czyniliśmy w modelu Cournota, czy Stackelberga to możemy na każdej prostej cena-zbyt znaleźć taki punkt, który maksymalizuje zysk 1 producenta. Prezentuja to np. punkty R i S. Jeżeli chcemy znaleźć punkt maksymalizujący zysk na ostatniej (najbardziej oddalonej od poczatku układu współrzędnych prostej cena-zbyt, to punkt styczności wypadnie w M1. To że będzie on w porównaniu do swoich odpowiedników na niższych funkcjach cena-zbyt leżał na lewo od nich wynika z tego, że ta ostatnia prosta jest bardziej stroma od wszystkich poprzednich. Punkty leżące między M1 i M2 będą prezentowały optymalne wielkości produkcji i ceny 1 producenta, które gwarantują mu osiągnięcie maksymalnego zysku w przypadkach gdy 2 oferent ustali swoją cenę na niższym poziomie niż p_2max ale na tyle wysokim, że proste cena-zbyt 1 producenta nie będą dochodziły do osi y₁ ale kończyły się na prostej cena-zbyt określonej dla p_2max. Wtedy wszystkie punkty z odcinka M1 M2 będą również zaliczone do funkcji reakcji 1 duopolisty.

Przenieśmy teraz najważniejsze elementy z rys. 2 w nowy układ wspólrzędnych. Prezentuje to rys. 3.

Najpierw przenosimy w nowy układ współrzędnych prostą DE, czyli funkcję cena-zbyt dla p_2max. Patrząc na wzór 5 (
) możemy stwierdzić, że jeżeli p₁ = 0, to p_2max = c₂/b₂. Jeżeli p₁ zwiększamy to i p_2max rośnie. Cena pierwszego oferenta może rosnąć do wielkości wyznaczonej przez odpowiednią współrzędną punktu E. W ten sposób znajdujemy nowe położenie wspomnianej funkcji cena-zbyt.

Następnie znajdujemy położenie punktów M1' i M2', gdyż muszą one leżeć na prostej D'E' i jednocześnie znamy odpowiadające im wielkości p₁. Tak samo łatwo można ustalić nowe położenie punktu R. Wiemy, że p₂ = 0 a p₁ odczytujemy z rys. 3. W ten sposób możemy ustalić przebieg całej funkcji reakcji R1.

W dalszej kolejności wygodnie jest ustalić nowy przebieg fragmentu osi p₁ pomiędzy punktem E i (c₁/a₁). Nowe położenie E już mamy ustalone. Jest to punkt E'. Wystarczy teraz odnależć ten drugi punkt. Wiadomo, że p₂ jest wtedy równe 0. Na koniec przenieśmy tylko jedną izokwantę zysku, na której wcześniej zaznaczyliśmy punkty P, Q, S, T, W. Dla każdego z tych punktów z rysunku odczytujemy wielkość p₁. Tak samo mamy zaznaczone na nim wielkości p₂. Przenosimy punkt po punkcie. Wtedy możemy ustalić polożenie współrzędnych p₂ = 10 i p₂ = 20.

Przebieg funkcji reakcji danego producenta w nowym układzie współrzędnych zależy od fukcji kosztów i do preferencji przypisanych danemu wytwórcy. Obowiązują w tym względzie następujące reguły:

- im niższe koszty tym prosta realcji jest bardziej pozioma,

- im większe preferencje są przypisane danemu wytwórcy, tym prosta reakcji leży niżej.

Jeżeli to samo rozumowanie przeprowadzimy dla drugiego duopolisty i zechcemy umieścić je w takim jak ostatnio układzie współrzędnych, to na rysunku można to przedstawić następująco, co prezentuje rys. 4.

Jeżeli tak jak na poczatku założyliśmy obaj producenci będą zachowywać się autonomicznie, to wtedy obaj po pewnym czasie dojdą do punktu V i ustalą ceny mu odpowiadające. Tym samym zrealizują zyski przypisdane izoliniom zysku przechodzące przez ten punkt.

Jeżeli pierwszy producent będzie się zachowywał heteronomicznie a drugi nadal autonomicznie, to ten pierwszy będzie skłonny zejść ze swoje funkcji reakcji R1 na R2, by w ten sposób zwiększyć swój zysk w stosunku do Z osiąganego w V. Pierwszy duopolista zachowując się heteronomicznie osiągnie maksymalny zysk w punkcie W1. Uzasadnienie jest identyczne jak prezentowane w modelu von Stackelberga.

Jeżeli pierwszy producent będzie się zachowywał autonomicznie a drugi heteronomicznie, to wtedy ten ostatni osiągnie maksymalny zysk w punkcie W2.

Jeżeli obaj producenci dojdą do porozumienia i będą maksymalizować zysk, to wtedy wybiorą jeden z punktów, który leży na krzywej łączącej punkty M1' i M2', gdyż wtedy suma obu zysków osiągnie swoje maksimum. Jak się podzielą tym zyskiem teraz nie jesteśmy w stanie roztrzygnąć.

5

---