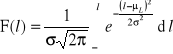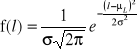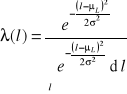NIEZAWODNOŚĆ OBIEKTÓW TECHNICZNYCH

Pojęcia niezawodności

Każdy wyrób techniczny produkowany jest z pewnym przeznaczeniem. Oznacza to, że w okresie eksploatacji powinien wypełniać określone funkcje przy spełnianiu wymagań zdefiniowanych przez jego projektanta lub wytwórcę. Zakres i rodzaj tych wymagań precyzowane są w dokumentacji technicznej maszyny w postaci podstawowych parametrów pracy. W przypadku samochodu mogą to być np.: moc silnika, prędkość maksymalna, zużycie paliwa itp., w przypadku komputera - pobór prądu, pojemność pamięci, szybkość działania, jakość (rozdzielczość i czas odświeżania) monitora itp.

Zdolność obiektu technicznego do spełniania powierzonych mu funkcji zgodnie z założonymi warunkami charakteryzuje jego niezawodność. Niezawodność jest więc cechą całego obiektu technicznego, np. maszyny. Niemalże w każdym obiekcie można wyróżnić jego układy funkcjonalne, zespoły czy nawet elementy, dla których również mogą być wyznaczone funkcje i wymagania techniczne. Pewien zakres funkcji może być realizowany nie przez pojedyncze maszyny, lecz zbiór jednorodnych lub różnych maszyn pracujących jako system. Także dana maszyna może być traktowana jako system złożony z zespołów lub układów funkcjonalnych. Dlatego przy omawianiu niezawodności wygodne jest używanie pojęcia obiektu technicznego, rozumianego, w zależności od potrzeb, jako pojedynczy element, zespół, układ, kompletna maszyna lub zbiór maszyn. Taki sposób podejścia pozwala na uogólnienie rozważań nad niezawodnością obiektów technicznych w postaci dyscypliny naukowej.

Teoria niezawodności jest to dyscyplina naukowa która zajmuje się badaniami występowania i przewidywania uszkodzeń oraz określaniem metod zapewnienia żądanej niezawodności obiektów technicznych. Należy podkreślić, że niezawodność obiektu jest kształtowana we wszystkich fazach jego istnienia: konstrukcji, produkcji i eksploatacji. Wynika stąd ogromna rola badań niezawodności dla powstania obiektu technicznego o wysokich cechach niezawodności, jak również widoczne są szerokie możliwości jej kształtowania także przez eksploatatora. Teoria niezawodności, jak każda dyscyplina naukowa, posługuje się określonym zakresem pojęć podstawowych, które wymagają ścisłego zdefiniowania, przede wszystkim niezawodności jako właściwości obiektu technicznego.

Niezawodność obiektu technicznego jest to właściwość polegająca na jego zdolności do spełniania wyznaczonych mu funkcji zgodnych z przeznaczeniem w danych warunkach i czasie eksploatacji.

Powyższa definicja wskazuje, że niezawodność może być rozpatrywana w odniesieniu do obiektu użytkowanego zgodnie z przeznaczeniem. Same wymagania mogą dotyczyć funkcjonowania lub zachowania zdatności przez określoną wielkość miary eksploatacji, wykonania określonej ilości pracy, spełnienia zadanej misji itp. Podkreśla się zależność niezawodności od warunków i czasu eksploatacji. Warunki eksploatacji, w odniesieniu do maszyny, są określone przez warunki atmosferyczne, obciążenia, jakość zasilania a także technikę użytkowania i obsługi. Rola czynnika czasu jest również istotna dla maszyn, użytkowanych i obsługiwanych na ogół ze zmienną intensywnością w długich okresach czasu.

Jeżeli wielkością charakteryzującą zdolność obiektu technicznego do spełniania stawianych mu wymagań jest prawdopodobieństwo spełnienie tych wymagań to niezawodność może być rozumiana jako prawdopodobieństwo, że obiekt będzie prawidłowo spełniał swoje zadania w danych warunkach przez określony czas. Wskazuje to, że niezawodność jest wielkością losową, a jej badanie i określenie musi być oparte na metodach probabilistycznych i statystyki matematycznej.

Jeśli prawidłowe spełnianie zadań przez obiekt techniczny nazwać po prostu sukcesem to można sformułować najkrótszą chyba definicję niezawodności: niezawodność jest to prawdopodobieństwo sukcesu.

Przy określaniu niezawodności konieczne jest jednoznaczne zdefiniowanie stanu niezawodnościowego obiektu. Dla oceny niezawodności maszyn najczęściej przyjmuje się założenie dwustanowości, co znacznie upraszcza analizę ich niezawodności w eksploatacji. Wyróżnia się tutaj stany zdatności i niezdatności. Zdatność jest to stan obiektu, w którym ma on zdolność wykonywania wyznaczonych mu funkcji zgodnie z parametrami określonymi w dokumentacji technicznej. Zdatność i niezdatność są stanami chwilowymi, a niezawodność - właściwością obiektu w czasie. Stany zdatności i niezdatności są jednoznacznie zdefiniowane przez wymagania zawarte w dokumentacji technicznej, a przejścia między nimi nazywają się uszkodzeniem i naprawą. Czasem zachodzi jednak uzasadniona technicznie potrzeba stosowania dodatkowych stanów technicznych i pojęć, np. stanów sprawności i niesprawności technicznej. Stan sprawności technicznej jest wtedy stanem, w którym parametry określające pewne właściwości maszyny związane z jej pracą nie przekraczają pewnych dopuszczalnych wartości granicznych. Wówczas także zdatność może być rozumiana jako tzw. zdatność zadaniowa, tj. zdolność obiektu do wykonywania pewnych tylko funkcji ze zbioru tych, do realizacji których został przeznaczony. W zależności od potrzeb można wyróżnić także inny zbiór stanów niezawodnościowych obiektów np.:

• obiekt zdatny i użytkowany;

• obiekt zdatny, oczekujący na użytkowanie;

• obiekt niezdatny, oczekujący na obsługę;

• obiekt niezdatny, obsługiwany.

Niezawodność można więc definiować jako prawdopodobieństwo, że obiekt będzie zdatny (sprawny technicznie) dla określonej wartości miary jego eksploatacji, a biorąc pod uwagę to, że stany niezawodnościowe obiektu określone są przedziałami wartości określonych parametrów pracy obiektu jako prawdopodobieństwo, że wartości parametrów określających istotne właściwości obiektu nie przekroczą dla określonej wartości miary jego eksploatacji dopuszczalnych granic w określonych warunkach eksploatacji

Niezawodność jest właściwością ogólną obejmującą takie cechy składowe jak: poprawność działania, trwałość, naprawialność i zachowawczość.

Poprawność działania (nieuszkadzalność, bezawaryjność) jest to właściwość obiektu polegająca na zachowaniu zdolności do pracy w ciągu określonego przedziału miary eksploatacji bez nieplanowych, wymuszonych uszkodzeniami przestojów. Poprawność działania może być mierzona czasem pracy maszyny bez zakłóceń (uszkodzeń), przy czym nie uwzględnia się tu przerw w pracy przeznaczonych na obsługi planowe. Miarą poprawności działania jest także prawdopodobieństwo, że maszyna rozpoczynająca pracę wykona ją do zamierzonego końca, np. pojazd wysłany w trasę powróci do miejsca postoju.

Trwałość jest to właściwość obiektu technicznego polegająca na zachowaniu w wymaganych granicach głównych parametrów roboczych określających jego stan graniczny. Trwałość jest mierzona ilością wykonanej pracy przez obiekt, np. dla pojazdu - przebiegiem. Nie powinna być utożsamiona z okresem eksploatacji, który oznacza kalendarzowy przedział czasu do chwili osiągnięcia przez obiekt stanu granicznego w danym systemie eksploatacji. Można stwierdzić, że trwałość „zużywa się” w okresie eksploatacji.

Stan graniczny określony jest niemożliwością techniczną lub niecelowością techniczną i ekonomiczną dalszej eksploatacji obiektu w systemie ze względu na wyjście podstawowych jego parametrów technicznych poza ustalone granice. Podstawowe (robocze) parametry techniczne charakteryzują zdolność obiektu do wykonywania funkcji i są ustalone w danym systemie eksploatacji. Parametry pomocnicze (drugorzędne) charakteryzują jego fizykochemiczne właściwości jako elementu w systemie. Z chwilą osiągnięcia stanu granicznego obiekt techniczny podlega kasacji. Oceny stanu granicznego należy dokonywać z uwzględnieniem kryteriów fizycznych, ekonomicznych i środowiskowych.

Trwałość jest określana przez rzeczywiście wykonaną ilość pracy, zaś ilość pracy przewidzianej do wykonania przez obiekt (narzuconej arbitralnie) do osiągnięcia stanu granicznego lub naprawy głównej można powiązać z resursem.

Naprawialność jest to właściwość obiektu technicznego polegająca na przystosowaniu go do odnowy stanu zdatności przez zapobieganie i usuwanie uszkodzeń drogą obsług i napraw. Zatem naprawialność oznacza zbiór właściwości określających pracochłonność i koszt obsług, łatwość dostępu, podatność diagnostyczną (przygotowanie do wykrywania uszkodzeń).

Zachowawczość jest to właściwość obiektu polegająca na zachowaniu ustalonych wartości wskaźników eksploatacyjnych w trakcie i po upływie okresu przechowywania i transportu. Cecha ta określa zatem stopień przystosowania obiektu do przechowywania (i transportu), odporność na działanie czynników środowiska, intensywność procesów starzeniowych. Jest cechą istotną w odniesieniu do maszyn, które są przechowywane przez długie okresy czasu jako zapas eksploatacyjny. Z zachowawczością związana jest także pracochłonność czynności przygotowawczych, zabiegów obsługowych podczas przechowywania oraz uruchomienia po okresie przechowywania.

Niezawodność stanowi jedną z najbardziej istotnych cech pojęcia jakości, która obejmuje ogół cech wyrobu, określających stopień spełniania przez niego wymagań użytkownika, m. in.: koszt, ekonomię eksploatacji, funkcjonalność, efektywność, ergonomię (dostosowanie do właściwości psychofizycznych człowieka), estetykę. W odniesieniu do wyrobów przemysłowych określa się jakość projektową i jakość wykonania.

Analiza niezawodności pozwala na porównanie właściwości obiektów technicznych danego typu, np. pojazdów różnych marek. W przypadku obiektów złożonych o ich niezawodności decyduje zazwyczaj niewielka liczba elementów stanowiących główne przyczyny uszkodzeń, zatrzymań, napraw i spadku gotowości eksploatacyjnej. Badanie niezawodności pozwala na określenie tzw. „słabych miejsc” i wskazuje potrzebę podjęcia przedsięwzięć konstrukcyjnych, technologicznych lub eksploatacyjnych mających na celu poprawę niezawodności obiektów złożonych. Pozwala także na planowanie optymalnej wielkości zapasów części zamiennych.

Podstawowe charakterystyki i parametry niezawodności

Charakterystyki i parametry niezawodności stanowią ilościową miarę cech niezawodności. Uszkodzenia obiektów mają charakter losowy, a stąd ich opis może być podany za pomocą odpowiednich rozkładów prawdopodobieństwa i ich parametrów. Ilość wykonanej pracy przez maszyną, zależnie od jej typu, jest określana przez różne miary eksploatacyjne: czas pracy, przebieg, liczbę włączeń, itp.. W teorii niezawodności ogólną miarą eksploatacyjną jest resurs poprawnej pracy, który jest zmienną losową ciągłą. Dla maszyn resurs można wyrazić za pomocą indywidualnej miary eksploatacji (np. przebieg dla pojazdu) lub ogólnie czasem pracy, i w efekcie Resurs poprawne pracy będzie oznaczany odpowiednio jako zmienne losowe L i T.

W teorii niezawodności wyróżnia się dwa typy obiektów technicznych:

• nienaprawialne - zwykle proste, pracujące do chwili uszkodzenia (np. żarówka, bezpiecznik); dla tych obiektów poprawność działania i trwałość oznaczają tę samą cechę niezawodności;

• naprawialne - zwykle złożone, po wystąpieniu uszkodzenia podlegające naprawie w celu odtworzenia stanu zdatności.

Podstawowe charakterystyki niezawodności opisują niezawodność obiektów nienaprawialnych. Są stosowane jednak także dla naprawialnych w następujących przypadkach:

• w okresie do wystąpienia pierwszego uszkodzenia;

• dla okresów pomiędzy kolejnymi uszkodzeniami (przy założeniu, że podczas naprawy następuje pełne odtworzenie potencjału eksploatacyjnego obiektu);

• w odniesieniu do całego okresu eksploatacji urządzenia, tzn. pomijamy fakt występowania uszkodzeń i napraw.

Funkcja zawodności F(l) określa prawdopodobieństwo wystąpienia uszkodzenia obiektu w przedziale miary eksploatacji (0, l). Jest ona więc dystrybuantą miary eksploatacji i w sensie probabilistycznym oznacza prawdopodobieństwo, że zmienna losowa L przyjmie wartość nie większą od l:

Dystrybuanta określa zawodność obiektu technicznego.

Funkcja niezawodności R(l) określa prawdopodobieństwo, że obiekt nie ulegnie uszkodzeniu w przedziale miary eksploatacji (0, l), czyli, że zmienna losowa L przyjmie wartość nie mniejszą od l:

Na podstawie przytoczonych definicji łatwo zauważyć, że

Przykładowy przebieg funkcji zawodności i niezawodności przedstawiono obok. Funkcja zawodności, jak wynika ze znanych własności dystrybuanty, jest funkcją niemalejącą i wskazuje, że wraz ze zwiększeniem resursu sprawnej pracy dowolnego obiektu technicznego, wzrasta prawdopodobieństwo jego uszkodzenia

W oparciu o funkcje zawodności i niezawodności można zdefiniować funkcję rozkładu gęstości prawdopodobieństwa powstania uszkodzenia f(l). Określa ona przypadające na jednostkę miary eksploatacji prawdopodobieństwo powstania uszkodzenia w chwili, gdy mara ta jest równa l:
.

Oczywiście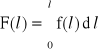
i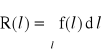

W praktyce nie zawsze potrzebna jest znajomość całego przebiegu funkcji charakteryzujących niezawodność obiektu. Często wystarcza znajomość tylko pewnych liczbowych wartości charakteryzujących zmienne losowe L lub T, czyli parametrami niezawodności. Podstawowymi parametrami niezawodności są:

oczekiwany resurs poprawnej pracy _L, definiowany jako wartość oczekiwana (przeciętna) zmiennej losowej L (lub T):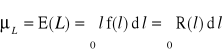

• odchylenie standardowe σ resursu poprawnej pracy, które jest miarą rozproszenia zmiennej losowej wokół jej wartości średniej. Odchylenie standardowe jest pierwiastkiem kwadratowym z wariancji:
  

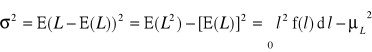
Wymienionym parametrom można przypisać pewien sens fizyczny. Średni resurs poprawnej pracy pozwala na ocenę jakości konstrukcji i trwałości materiałów maszyny. Odchylenie standardowe charakteryzuje jakość technologii produkcji i jakość eksploatacji maszyny.

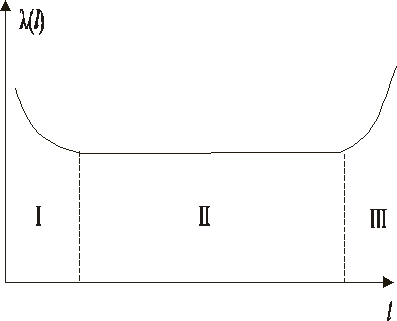
Bardzo ważną charakterystyką niezawodności jest funkcja intensywności uszkodzeń λ(l). Określa ona przypadającą na jednostkę miary eksploatacji l wartość prawdopodobieństwa warunkowego Q(l, l+l) uszkodzenia obiektu w przedziale miary eksploatacji [l, l+l) jeżeli pracował on poprawnie do wartości miary eksploatacji l (czyli pod warunkiem, że nie uległ on uszkodzeniu w przedziale miary eksploatacji (0, l)):

Zauważmy, że zgodnie z definicją, prawdopodobieństwo warunkowe poprawnej pracy (nie występowania uszkodzenia) obiektu w przedziale (l, l+Δl) może być określone za pomocą funkcji niezawodności:
. Ponieważ suma prawdopodobieństw warunkowych jest równa
to otrzymuje się:

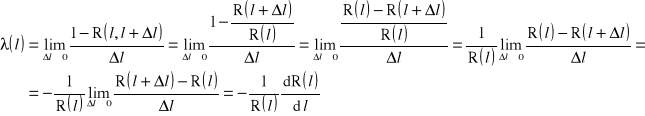
czyli równanie różniczkowe zwyczajne pierwszego rzędu, które można rozwiązać metodą rozdzielenia zmiennych:

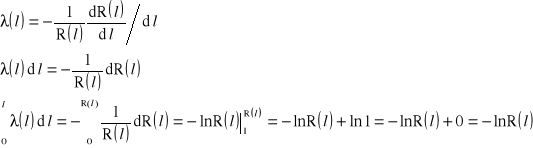
czyli
lub

Znając zależności pomiędzy funkcjami F(l), R(l) i f(l) oraz parametrem _L uzyskuje się:
oraz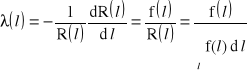
oraz
oraz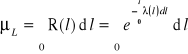

Jak widać funkcja niezawodności obiektu technicznego R(l) jest znana, gdy znana jest jego funkcja intensywności uszkodzeń λ(l). Funkcja ta ma na ogół przebieg złożony i różny dla różnych typów maszyn. Można jednak przyjąć, że w wielu przypadkach ma przebieg jak przedstawiony obok. Wówczas można wyróżnić trzy podokresy eksploatacji obiektu technicznego.

Okres I początkowy, nazywany okresem docierania obiektu, charakteryzuje się dużą intensywnością uszkodzeń, których przyczyną są błędy produkcyjne, takie jak wadliwy montaż, niewłaściwa technologia, ukryte wady materiału, itp. Okres docierania maszyny powinien zbiegać się z okresem gwarancyjnym, a ilość uszkodzeń w tym okresie może być zmniejszona przez efektywnie funkcjonującą kontrolę jakości.

Okres II normalnej, stałej eksploatacji, w którym dominują uszkodzenia przypadkowe (mają one charakter losowy) i w związku z tym intensywność uszkodzeń jest w przybliżeniu stała.

Okres III końcowy, nazywany okresem przyspieszonego zużycia starzeniowego, w którym intensywność uszkodzeń znacznie wzrasta wskutek osiągania przez obiekt stanu granicznego.

Zwykle najdłużej trwającym i najważniejszym dla eksploatatora jest okres II eksploatacji obiektu, dla którego można przyjąć
, co daje:

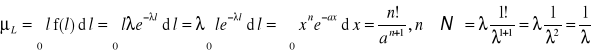
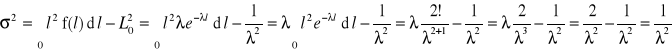
czyli rozkład wykładniczy. Podstawową zaletą rozkładu wykładniczego jest jego prostota, gdyż jest rozkładem jednoparametrowym. Zakres jego praktycznych zastosowań jest ograniczony - opisuje dobrze jedynie niezawodność obiektów niestarzejących się, tzn. zgodnie z przyjmowanym wyżej założeniem funkcja intensywności uszkodzeń jest stała w czasie eksploatacji. Uszkodzenie obiektu następuje w wyniku działania przyczyn losowych, a nie wskutek zmian jego stanu wraz z upływem okresu eksploatacji.

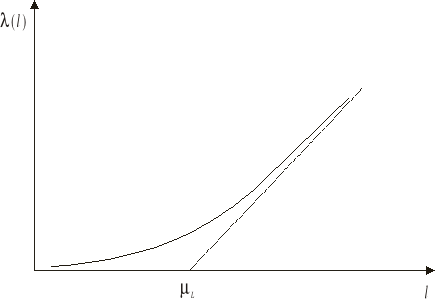
Wykres dystrybuanty F(l) i funkcji gęstości f(l) rozkładu wykładniczego przedstawiono obok. Jak widać oczekiwany resurs poprawnej pracy obiektu
można odczytać z tych wykresów jako współrzędną l punktu przecięcia stycznej do wykresów F(l) lub f(l) w punkcie l = 0 z prostymi F(l) = 1 lub f(l) = 0.

Dla
zachodzi

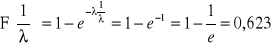
oraz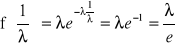
.

Większość obserwowanych rozkładów uszkodzeń maszyn można opisać rozkładem Weibulla, czyli takim, że funkcję niezawodności można zapisać w postaci
, gdzie α i β są odpowiednio współczynników kształtu i skali rozkładu Weibulla. Rozkład Weibulla jest rozkładem dwuparametrowym i jego szczególnym przypadkiem (dla α = 1) jest rozkład wykładniczy. Przy odpowiednim doborze wartości parametrów α i β uzyskuje się lepszą zgodność z danymi eksperymentalnymi niż w przypadku rozkładu wykładniczego, zależnego tylko od jednego parametru λ. Dla rozkładu Weibulla:

Funkcja intensywności uszkodzeń, zależnie od wartości parametru α, może być funkcją rosnącą (α > 1), stałą (α = 1) lub malejącą (0 < α < 1).

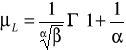
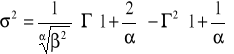
gdzie: Γ(x) jest funkcją gamma Eulera argumentu x. Na rysunku obok przedstawiono wykresy funkcji gęstości rozkładu Weibulla dla β = 1 i wybranych wartości parametru α = 0,5; 1; 2 i 4

Do opisu funkcji niezawodności wykorzystuje się też czasami rozkłady:

Pareto

Frecheta

potęgowy

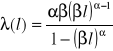
jednorodny

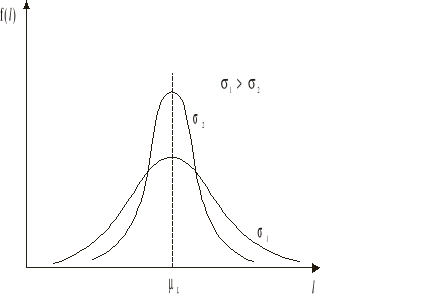
Uszkodzenia spowodowane bodźcami kumulującymi się (procesy starzenia, zużycie) w wielu przypadkach można dostatecznie dobrze opisywać rozkładem normalnym, zwłaszcza gdy σ << _L (odchylenie standardowe jest dużo mniejsze od wartości oczekiwanej resursu poprawnej pracy).

Funkcja zawodności (dystrybuanta) rozkładu normalnego ma postać a funkcja gęstości prawdopodobieństwa Przykładowe wykresy funkcji gęstości rozkładu normalnego przedstawiono obok

Funkcję niezawodności można zapisać zmieniając granice całkowania jako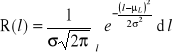

Funkcja intensywności uszkodzeń ma postać , jest funkcją rosnącą i ma asymptotę ukośną Jej wykres przedstawiono obok

Wartość oczekiwana resursu poprawnej pracy _L i odchylenie standardowe tego resursu σ są parametrami rozkładu normalnego. W praktyce korzysta się z tablic standardowego rozkładu normalnego N(0,1), w którym wartość oczekiwana jest równa 0, zaś odchylenie standardowe 1. Rozkład standardowy uzyskuje się wprowadzając zmienną standaryzowaną
, zaś funkcja gęstości standaryzowanej zmiennej losowej X (funkcja Gaussa) ma postać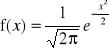

Funkcja Gaussa i dystrybuanta standaryzowanego rozkładu normalnego są stablicowane. Należy zauważyć, że rozkład normalny jest określony w zbiorze liczb rzeczywistych, zaś w zagadnieniach niezawodności zmienna losowa nie przyjmuje wartości ujemnych. Dlatego też w zastosowaniach praktycznych zamiast tego typu rozkładem należy posługiwać się tzw. rozkładem normalnym uciętym w zerze, zwłaszcza gdy nie jest spełniony warunek σ << _L

Dobór odpowiedniego typu rozkładu do opisu niezawodności danego obiektu technicznego na podstawie wyników badań jego niezawodności następuje w oparciu o znane procedury statystyki matematycznej (np. testy zgodności).

Modele odnowy i charakterystyki obiektów naprawialnych

W teorii niezawodności pod pojęciem odnowy rozumie się przywrócenie stanu zdatności obiektowi, który uległ uszkodzeniu. Odnowa może polegać na wymianie uszkodzonego elementu lub takiej jego naprawie, która przywraca wszystkie pierwotne właściwości. Przyjmujemy, że proces odnowy w pełni odtwarza zdolność do spełniania funkcji (tzw. potencjał eksploatacyjny) przez złożony obiekt techniczny. Wyróżnia się dwa typy modelu odnowy: model odnowy natychmiastowej i odnowy o skończonym czasie trwania.

Model odnowy natychmiastowej ma zastosowanie w przypadku, gdy czas przebywania obiektu w naprawie jest pomijalnie mały w porównaniu z czasem jego użytkowania lub fakt jego uszkodzenia nie ma wpływu na funkcjonowanie systemu, w którym może on być zastąpiony w okresie naprawy przez inny egzemplarz obiektu tego samego typu (system z rezerwą nieobciążoną). Obiekt pracuje więc od chwili początkowej do chwili pierwszego uszkodzenia, która jest jednocześnie chwilą pierwszego odnowienia i dalej od tej chwili odnowienia do chwili drugiego uszkodzenia, która jest jednocześnie chwilą drugiego odnowienia itd. Model procesu eksploatacji takiego obiektu przedstawiono poniżej. Dla maszyny wygodnie jest posługiwać się tu miarą jej eksploatacji L. Na rysunku l₁, l₂, l₃, ... określają wartości miary eksploatacji, dla których nastąpiło uszkodzenie i odnowa maszyny. Zmienne losowe L₁, L₂, L₃, ... oznaczają wielkości miary eksploatacji maszyny między kolejnymi uszkodzeniami i tworzą strumień użytku.

Jeżeli w procesie odnowy następuje pełne odtworzenie potencjału eksploatacyjnego, to zmienne losowe L₁, L₂, L₃, ... są niezależne i mają jednakowy rozkład, a strumień użytku nazywa się strumieniem prostym. Jeżeli dodatkowo rozkład ten jest rozkładem wykładniczym z parametrem  (nazywanym intensywnością użytkowania), dla którego funkcja zawodności
i wartość oczekiwana
, to strumień nazywa się strumieniem Poissona.

Stan procesu odnowy maszyny określa liczba uszkodzeń (odnów) K(l), która też jest zmienną losową i funkcją resursu l. Istnieje oczywisty związek między liczbą uszkodzeń a zużytą przez maszynę wielkością miary eksploatacji do n-tego uszkodzenia:

P[K(l) ≥ n] = P(l_n < l) = P(L₁ + L₂ + ... + L_n < l) = F_n(l)

gdzie F_n(l) jest dystrybuantą sumarycznego przebiegu do n-tego uszkodzenia i odnowienia. Należy przy tym zauważyć, że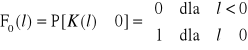

Zatem prawdopodobieństwo, że do danego przebiegu l wystąpiło dokładnie n uszkodzeń jest równe

Podstawową charakterystyką procesu odnowy jest tzw. funkcja odnowy H(l), która jest wartością oczekiwaną liczby uszkodzeń:

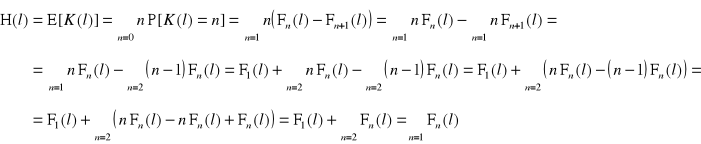
Jeżeli znana jest funkcja odnowy, to oczekiwaną wartość liczby uszkodzeń w przedziale miary eksploatacji (l₁, l₂) można obliczyć ze wzoru

Charakterystykę określającą oczekiwaną liczbę uszkodzeń przypadającą na jednostkę miary eksploatacji, nazywa się funkcją gęstości odnowy:

W przypadku, gdy niezawodność maszyny opisana jest rozkładem wykładniczym z parametrem  = const otrzymuje się: H(l) = λl i h(l) = λ

Model odnowy trwającej w czasie należy rozpatrywać, gdy czas naprawy nie jest pomijalnie krótki w porównaniu z czasem przebywania obiektu w stanie zdatności. Oznacza to, że system, w którym maszyna jest eksploatowana, „odczuwa” skutki jej przebywania w naprawie. Obiekt pracuje od chwili początkowej do chwili pierwszego uszkodzenia, następnie jest odnawiany do chwili pierwszego odnowienia, dalej od tej chwili odnowienia do chwili drugiego uszkodzenia znów pracuje, potem znów jest odnawiany itd. Model procesu eksploatacji takiego obiektu przedstawiono poniżej. Celowe jest tutaj przyjęcie czasu jako miary eksploatacji (resursu poprawnej pracy). Łuki umieszczone nad osią czasu przedstawiają przedziały czasu przebywania obiektu w stanie zdatności, łuki poniżej osi czasu - przedziały czasu przebywania w odnowie. Zmienne losowe T₁^', T₂^',... wyrażają kolejne czasy trwania stanów zdatności, a T₁^”, T₂^”,... czasy trwania stanów niezdatności i odnowień. Chwile czasu t₁^', t₂^',... są chwilami kolejnych uszkodzeń, a chwile t₁^”, t₂^”,... są chwilami kolejnych odnowień. Gdy w procesie odnowy następuje pełne odtwarzanie stanu zdatności maszyny, to wszystkie zmienne losowe T_i^' i T_i^”,... są niezależne i mają jednakowe rozkłady, najczęściej przyjmowane jako wykładnicze o parametrach odpowiednio  (intensywność użytku) dla użytkowania i  (intensywność odnowy) dla odnowy, dla których dystrybuanty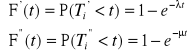
oraz wartości oczekiwane czasów zdatności i odnowy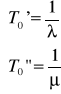

Kolejne chwile wystąpienia uszkodzeń można wyrazić jako
, zaś kolejne chwile odnowień jako

Oczywiste jest, ze powinno się dążyć do minimalizacji czasów trwania stanów niezdatności i odnowień ze względu na koszty z tym związane, czyli koszty samego odnowienia oraz koszty wynikające z wyłączenia obiektu z użytkowania (zmniejszenie możliwości operacyjnych przedsiębiorstwa oraz nakłady na dodatkowe obiekty pracujące (użytkowane) w zastępstwie obiektów odnawianych (obsługiwanych)).

Rozpatrywany model odnowy można opisać za pomocą charakterystyk analogicznych jak dla modelu odnowy natychmiastowej. Jednak bardziej przydatną dla eksploatatora informację zawiera charakterystyka niezawodności określająca tzw. współczynnik gotowości k_g(t). Jest on równy prawdopodobieństwu tego, że w chwili t obiekt znajduje się w stanie zdatności: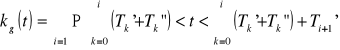
. Najczęściej posługujemy się jego wartością stacjonarną, asymptotyczną:
, gdzie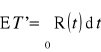
jest oczekiwanym czasem poprawnej pracy a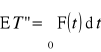
oczekiwanym czasem odnowy (czyli stosunkiem oczekiwanego czasu poprawnej pracy do sumy czasów pracy i odnowy (udziałem czasu zdatności w ogólnym czasie eksploatacji)). Dla odpowiednio dużej liczby n cykli praca-odnowa obie wartości oczekiwane można estymować za pomocą wartości średnich kolejnych czasów zdatności i odnowień:
i

Dla przypadku możliwości wykorzystania rozkładu wykładniczego do opisywania czasów trwania stanów zdatności i odnów otrzymuje się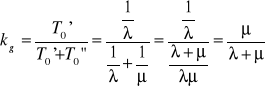

Współczynnik k_g jest obliczany dla pełnego czasu eksploatacji (dla pełnego czasu trwania przebywania maszyny w systemie odnowy) to określa nie tylko niezawodność maszyny, ale także właściwości systemu eksploatacji (uwzględnia czasy oczekiwania na obsługę oraz włączenia do użytkowania po obsłudze). Czasem celowe jest jednak posługiwanie się parametrem niezawodności zależnym jedynie od właściwości maszyny. Jest nim współczynnik gotowości technicznej:
gdzie T_eo jest oczekiwanym czasem efektywnej obsługi.

Maszyna jako system w sensie niezawodności

Jako system w sensie niezawodności rozumiemy zbiór elementów tworzących razem złożony obiekt i realizujących wspólny cel działania. Zakładamy, że niezawodność elementów jest znana i każdy element uszkadza się niezależnie, tzn. że uszkodzenie dowolnego elementu lub grupy elementów nie zmienia niezawodności innych elementów. Powyższe stwierdzenie oznacza, że elementy są niezależne w sensie niezawodności. Oczywiście niezawodność pojedynczych elementów ma wpływ na niezawodność całego obiektu (zbioru elementów).

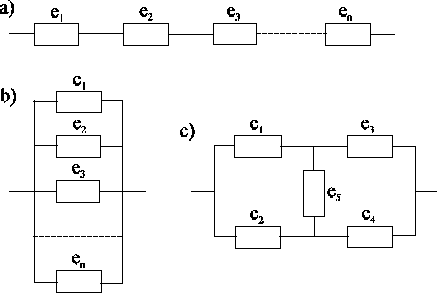
Elementy systemu mogą pracować w różnych układach funkcjonalnych, wyrażających rodzaje połączeń, zależności między nimi. Dla rozpatrywania tych połączeń i niezawodności systemów dogodnie jest stosować analogię układów elektrycznych, w których przepływa prąd, jak to pokazano na rysunku poniżej. W praktyce mogą występować bardziej złożone kombinacje połączeń elementów systemu.

Schemat systemu niezawodności o strukturze: a) szeregowej; b) równoległej; c) mostkowej

Elementy systemu są połączone szeregowo (w sensie niezawodności), jeżeli uszkodzenie dowolnego elementu powoduje uszkodzenie całego systemu. Aby taki system pracował poprawnie dla wartości miary eksploatacji z przedziału (0,l), konieczne jest aby w tym przedziale poprawnie pracowały wszystkie jego elementy. Stąd funkcję niezawodności systemu można wyrazić poprzez charakterystyki elementów jako iloczyn funkcji niezawodności elementów składowych: R(l) = R₁(l) R₂(l) ... R_n(l)

Można więc zapisać, że funkcja intensywności uszkodzeń systemu o strukturze szeregowej jest sumą funkcji intensywności uszkodzeń elementów składowych: λ(l) = λ₁(l) + λ₂(l) + ...+λ_n(l)

Jeżeli wszystkie elementy systemu mają jednakową funkcję niezawodności (R₁(l) = R₂(l) = ... = R_n(l) = R₀(l)), to funkcja niezawodności systemu
. Jeżeli wszystkie elementy systemu mają jednakową funkcję intensywności uszkodzeń (λ₁(l) = λ₂(l) = ... = λ_n(l) = λ₀(l)), to funkcja intensywności uszkodzeń systemu λ(l) = nλ₀(l).

Jeżeli niezawodność elementów systemu można opisać za pomocą rozkładów wykładniczych to intensywność uszkodzeń systemu jest równa λ = λ₁ + λ₂ + ...+λ_n, w szczególności gdy intensywność uszkodzeń elementów systemu jest jednakowa (λ₁ = λ₂ = ... = λ_n = λ₀), to intensywność uszkodzeń systemu λ = nλ₀ oraz funkcja niezawodności systemu ma postać

Oczekiwany resurs _L poprawnej pracy systemu składającego się z n niezależnych elementów można wyrazić za pomocą oczekiwanych resursów poprawnej pracy elementów:

Jeżeli niezawodność elementów systemu można opisać za pomocą rozkładów wykładniczych to oczekiwany resurs _L poprawnej pracy systemu składającego się z n niezależnych elementów można wyrazić za pomocą oczekiwanych resursów poprawnej pracy elementów: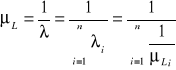
, w szczególności gdy intensywność uszkodzeń elementów systemu jest jednakowa λ₀, to oczekiwany resurs _L poprawnej pracy systemu
, gdzie _Lo jest oczekiwanym resursem poprawnej pracy elementu składowego systemu

Elementy systemu są połączone równolegle (w sensie niezawodności), jeżeli uszkodzenie systemu następuje tylko wtedy, gdy uszkodzeniu ulegną wszystkie jego elementy. Aby taki system pracował poprawnie dla wartości miary eksploatacji z przedziału (0,l), wystarczy aby w tym przedziale poprawnie pracował choć jeden element. W tym przypadku funkcję zawodności systemu można wyrazić poprzez charakterystyki elementów jako iloczyn funkcji zawodności elementów składowych: F(l) = F₁(l) F₂(l) ... F_n(l)

Jeżeli wszystkie elementy systemy mają jednakową funkcję zawodności (F₁(l) = F₂(l) = ... = F_n(l) = F₀(l)), to funkcja zawodności systemu

Jeżeli niezawodność elementów systemu można opisać za pomocą rozkładów wykładniczych o identycznych intensywnościach uszkodzeń, to funkcja zawodności systemu ma postać

Można wykazać, że w tym przypadku oczekiwany resurs poprawnej pracy systemu składającego się z n niezależnych elementów jest równy
, a dla dużych wartości n:
gdzie c = 0,577...

Maszyna jest złożonym obiektem technicznym, w którym można wyróżnić szereg elementów, zespołów, czy układów funkcjonalnych. Realizują one określone funkcje, które łącznie zapewniają odpowiednie właściwości funkcjonalne maszyny. Niezawodność maszyny wynika z niezawodności jej układów składowych, pracujących jako elementy systemu o określonej strukturze niezawodnościowej.

Metody wyznaczania charakterystyk niezawodności

Badania niezawodności maszyn prowadzone są dla ściśle określonych celów, wynikających z potrzeb producenta lub eksploatatora. Szczególne znaczenie poznawcze i aplikacyjne mają badania realizowane w normalnych warunkach eksploatacji, w których maszyna podlega oddziaływaniu czynników naturalnych wymuszających jej starzenie. W wyniku przeprowadzonych badań eksploatator lub producent uzyskuje informację o zaistniałych uszkodzeniach maszyny (lub jej układów funkcjonalnych i elementów) dla dyskretnych wartości miary eksploatacji lub czasu.

Do wyznaczenia empirycznych charakterystyk i parametrów niezawodności niezbędny jest zbiór informacji zawierający rejestracje chwil powstawania uszkodzeń poszczególnych elementów badanej próby maszyn. Wielkość badanej próby oraz wartości miary eksploatacji, dla których wykonywane są badania w zasadniczy sposób wpływają na dokładność oszacowań niezawodności, dlatego są one składowymi planu badań niezawodności. Na plan badań niezawodności składają się trzy elementy: {N, Y, Z}:

N - liczba badanych obiektów w próbie

Y - sposób badania:

B - bez wymiany uszkodzonych elementów na nowe

W - z wymianą uszkodzonych elementów na nowe

Z - kryterium zakończenia badań:

T - do z góry zadanej wartości miary eksploatacji

R - do wystąpienia określonej liczby uszkodzeń

(T,R) - do zadanej wartości miary eksploatacji lub do wystąpienia określonej liczby uszkodzeń w zależności co pierwsze wystąpi, przy czym wartości T i R mogą być stałe lub funkcjami miary eksploatacji albo czasu kalendarzowego

Wybór odpowiedniego planu eksploatacji spośród możliwych {N, B, T}, {N, B, R},{N, B, (T,R)}, {N, W, T}, {N, W, R},{N, W, (T,R)} zależy od warunków techniczno-organizacyjnych, celu badań, charakteru obiektu badań i wymaganej dokładności oszacowania charakterystyk niezawodności. Np. dla obiektów nieodnawialnych stosuje się zwykle plany typu B, a dla obiektów odnawialnych stosuje się zwykle plany typu W. Najbardziej dokładne wyniki otrzymuje się dla obserwacji prowadzonych do chwili wystąpienia R = N uszkodzeń (do chwili uszkodzenia wszystkich badanych obiektów).

Wyniki badań niezawodności otrzymuje się w efekcie wyznaczenia eksperymentalnych wartości charakterystyk i parametrów niezawodności w funkcji miary eksploatacji. Omówione wcześniej funkcje i parametry niezawodności mają prostą interpretację statystyczną jeżeli prawdopodobieństwa odpowiednich zdarzeń zastąpi się częstością ich występowania w danej próbie (zbiorowości) obiektów tego samego typu dla badań typu B i R = N. Niech:

N - liczba obiektów badanych

n(l) - liczba obiektów znajdujących w stanie zdatności się dla danej wartości miary eksploatacji l

m(l) - liczba obiektów znajdujących się w stanie niezdatności dla danej wartości miary eksploatacji l

m(l) = n(l - l) - n(l) = m(l) - m(l - l) - liczba obiektów uszkodzonych w przedziale miary eksploatacji
(l - l, l)

Oczywiście: n(l) + m(l) = N

0 ≤ n(l) ≤ N i 0 ≤ m(l) ≤ N

n(0) = N i m(0) = 0

n(l - l) ≥ n(l) i m(l - l) ≤ m(l)

oraz:

- empiryczna funkcja zawodności (dystrybuanta przebiegu)

- empiryczna funkcja niezawodności

- empiryczna funkcja gęstości prawdopodobieństwa

- empiryczna funkcja intensywności uszkodzeń

- wartość oczekiwana resursu poprawnej pracy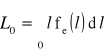

- wariancja resursu poprawnej pracy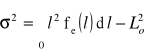

Ponieważ zwykle rejestracji dokonuje się dla dyskretnych wartości miary eksploatacji (np. co 1 miesiąc, 1 rok, 1000 km, 100 mth) to korzysta się z następujących wzorów:

N - liczba obiektów badanych

k - liczba obserwacji (badań) w trakcie eksploatacji

i - numer obserwacji (badania), i = 0 dla stanu początkowego (poprodukcyjnego, nowych maszyn, rozpoczynającego eksploatację), i = 1, ..., k dla właściwych badań w trakcie eksploatacji

n_i - liczba obiektów znajdujących się w stanie zdatności dla danej wartości miary eksploatacji l_i (dla i-tego pomiaru)

m_i - liczba obiektów znajdujących się w stanie niezdatności dla danej wartości miary eksploatacji l_i (dla i-tego pomiaru)

m_i-1,i = n_i-1 - n_i = m_i - m_i-1 - liczba obiektów uszkodzonych w przedziale miary eksploatacji (l_i-1, l_i) o długości l_i = l_i - l_i-1 (pomiędzy i-1-szym i i-tym pomiarem)

Oczywiście: n_i + m_i = N

0 ≤ n_i ≤ N i 0 ≤ m_i ≤ N

n₀ = N i m₀ = 0

n_i-1 ≥ n_i i m_i-1 ≤ m_i

oraz:

- empiryczna funkcja zawodności (dystrybuanta przebiegu)

- empiryczna funkcja niezawodności

- empiryczna funkcja gęstości prawdopodobieństwa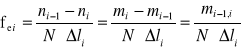

- empiryczna funkcja intensywności uszkodzeń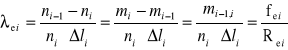

- wartość średnia (oczekiwana) resursu poprawnej pracy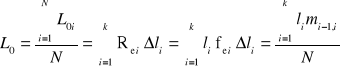

gdzie: L_0i - realizacja okresu zdatności przez i-ty obiekt;

- empiryczna wariancja resursu poprawnej pracy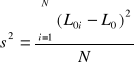

- przedział ufności dla wartości średniej przebiegu (L₀ - ΔL, L₀ + ΔL), gdzie
, gdzie t_α,N-1 jest wartością krytyczną rozkładu t-Studenta dla przyjętego prawdopodobieństwa α i N-1 stopni swobody. Poziom ufności 1-α oznacza prawdopodobieństwo, że wynik badania L₀ (uzyskana średnia) różni się od rzeczywistej wartości oczekiwanej _L nie więcej niż o ΔL: P(L₀ - ΔL ≤ _L ≤ L₀ + ΔL) = 1 - α. Im wyższa jest przyjęta wartość poziomu ufności 1-α, tym dłuższy jest przedział ufności.

Uzyskane rezultaty można przedstawić w postaci graficznej (najlepiej wykresów słupkowych), a tej podstawie założyć konkretny typ rozkładu opisujący niezawodność badanych maszyn. Np. jeżeli wykres empirycznej funkcji intensywności uszkodzeń jest stały, to można założyć, że niezawodność może być opisywana rozkładem wykładniczym. Oczywiście znanych jest wiele typów rozkładów i w celu wyboru najbardziej adekwatnego należy przeprowadzić wybrany test zgodności. Najczęściej wykorzystywany jest test zgodności χ² (Pearsona). Sposób weryfikacji jest następujący:

1) założyć określony typ rozkładu i oszacować jego parametry na podstawie dostępnych wyników badań eksperymentalnych;

2) dokonać podziału uzyskanych wyników badań według przedziałów miary eksploatacji na K rozłącznych klas o eksperymentalnej liczności n_k nie mniejszej niż 5;

3) dla każdej z klas wyznaczyć teoretyczną wartość prawdopodobieństwa p_k, że badana zmienna losowa L przyjmuje wartości l_k tworzące k-tą klasę (na podstawie funkcji gęstości lub dystrybuanty przyjętego rozkładu w kroku pierwszym, np. ze wzoru p_k = F(L_k+1) - F(L_k));

4) obliczyć teoretyczne liczności poszczególnych klas wyników równe N⋅p_k lub empiryczne prawdopodobieństwa znalezienia obserwacji w przedziale (L_k, L_k+1) równe
; gdzie N jest liczbą zarejestrowanych obserwacji (pomiarów, np. badanych maszyn dla badań realizowanych wg planów typu B i R = N);

5) obliczyć wartość statystyki

;

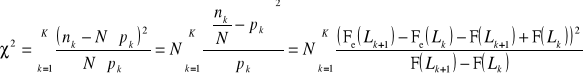
6) z tablic rozkładu χ² odczytać wartość graniczną χ_² dla założonego poziomu istotności α i liczby stopni swobody K - r - 1, gdzie r jest liczbą parametrów rozkładu szacowanych na podstawie wyników próby (np. 1 dla rozkładu wykładniczego, 2 dla rozkładu normalnego);

7) zweryfikować hipotezę, że niezawodność badanego obiektu ma założony rozkład:

- jeżeli χ² < χ_², to brak jest podstaw do odrzucenia hipotezy;

- jeżeli χ² ≥ χ_², to hipotezę należy odrzucić i ewentualnie kontynuować postępowanie w stosunku do innego typu rozkładu.

Z powyższego wynika, że im mniejsza jest obliczona wartość statystyki χ², tym przyjęta hipoteza jest bardziej wiarygodna, czyli obliczając wartość statystyki χ² dla kilku rozkładów najbardziej adekwatny jest ten, dla którego wartość tej statystyki jest najmniejsza.

Przykład

Podczas badań niezawodności maszyny zarejestrowano następujące liczby n_i uszkodzeń w wymienionych przedziałach miary eksploatacji l_i:

li	0 ÷ 0,5	0,5 ÷ 1,0	1,0 ÷ 1,5	1,5 ÷ 2,0	2,0 ÷ 2,5	2,5 ÷ 3,0	3,0 ÷ 3,5	3,5 ÷ 4,0	4,0 ÷ 4,5	4,5 ÷ 5,0	5,0 ÷ 6,0	6,0 ÷ 8,0	8,0 ÷ 10,0
ni	113	45	32	20	15	12	12	10	8	8	10	10	5

Wyznaczyć i przedstawić w postaci wykresów:

1. empiryczną dystrybuantę przebiegu (funkcję zawodności);

2. empiryczną funkcję niezawodności;

3. funkcję rozkładu prawdopodobieństwa przebiegu między uszkodzeniami;

4. empiryczną funkcję intensywności uszkodzeń;

5. wartość oczekiwaną przebiegu miedzy uszkodzeniami;

6. odchylenie standardowe przebiegu od wartości średniej;

7. za pomocą testu χ² określić, czy proces uszkodzeń może być opisany rozkładem wykładniczym.

Rozwiązanie:

Wyniki obliczeń empirycznych charakterystyk niezawodności samochodu ciężarowego, wymienionych w punktach a, b, c, d, wraz z danymi eksperymentalnymi zamieszczono w tabeli 4.2. Dla wartości przebiegu wymieniono w tabeli tylko granicę górną każdego przedziału przebiegu.

Tabela 4.2

Lp.	Li [tys. km]	ni	F (Li)	R (Li)	f (Li) [1/tys. km]	λ (Li) [1/tys. km]
1	0,5	113	0,377	0,623	0,753	0,753
2	1,0	45	0,527	0,473	0,300	0,481
3	1,5	32	0,633	0,367	0,213	0,450
4	2,0	20	0,700	0,300	0,133	0,364
5	2,5	15	0,750	0,250	0,100	0,333
6	3,0	12	0,790	0,210	0,080	0,320
7	3,5	12	0,830	0.170	0,080	0,381
8	4,0	10	0,863	0,137	0,067	0,392
9	4,5	8	0,890	0,110	0,053	0,390
10	5,0	8	0,917	0,083	0,053	0,485
11	6,0	10	0,950	0,050	0,033	0,400
12	8,0	10	0,983	0,017	0,017	0,333
13	10,0	5	1,000	0,000	0,008	0,500

a) Empiryczną funkcję zawodności wyznaczymy z zależności (4.55), którą można przekształcić stosując oznaczenia przykładu:

gdzie sumowane są liczby uszkodzeń pojazdów w poprzedzających przedziałach przebiegu do danego włącznie. Ogólna liczba zarejestrowanych danych eksperymentalnych:

;

Kolejne wartości dystrybuanty przebiegu są równe:

;

;

;

itd. Wykres funkcji zawodności przedstawiono na rys. 4.11.

Rys. 4.11. Wykres funkcji zawodności przebiegu między uszkodzeniami samochodu ciężarowego.

b) Funkcję niezawodności wyznaczymy korzystając z zależności:

R(l) + F(l) = 1

a stąd:

Wartości funkcji są zatem równe:

;

;

;

itd. Wykres funkcji niezawodności można łatwo otrzymać w wyniku przekształcenia wykresu funkcji zawodności - rys. 4.11.

c) Na podstawie (4.56) można zapisać wyrażenie określające wartości rozkładu prawdopodobieństwa przebiegu między uszkodzeniami - przypadające na jednostkę przebiegu prawdopodobieństwo wystąpienia uszkodzenia samochodu:

gdzie Δl_i jest wartością przedziału przebiegu, w którym stwierdzono n_i uszkodzeń. Jako jednostkę przebiegu przyjmiemy 1 tys. km.

Wykres funkcji przedstawiono na rys. 4.12.

Rys. 4.12. Rozkład prawdopodobieństwa przebiegu między uszkodzeniami samochodu ciężarowego.

d) Empiryczną funkcję intensywności uszkodzeń obliczymy według zależności (4.57):

gdzie N(l_i-1) jest liczbą pojazdów zdatnych na początku danego przedziału przebiegu (na końcu przedziału poprzedniego):

Rys. 4.13. Eksperymentalna funkcja intensywności uszkodzeń samochodu ciężarowego eksploatowanego w jednostce wojskowej.

e) Wartość oczekiwaną przebiegu obliczymy na podstawie wyrażenia (4.58):

gdzie: l_i - przyjmujemy równe średniej wartości przebiegu w danym przedziale (tabela 4.2) w tysiącach kilometrów;

p_i - prawdopodobieństwo wystąpienia przebiegu l_i równe przyrostowi dystrybuanty w danym przedziale przebiegu;

p_i = F (l_i) - F (l_i-1)

L_o = 0,25 ⋅ 0,377 + 0,75 ⋅ 0,150 + 1,25 ⋅ 0,106 + 1,75 ⋅ 0,067 + 2,25 ⋅ 0,050 + + 2,75 ⋅ 0,040 + 3,25 ⋅ 0,040 + 3,75 ⋅ 0,033 + 4,25 ⋅ 0,027 + 4,75 ⋅ 0,027 +  + 5,50 ⋅ 0,033 + 7,00 ⋅ 0,033 + 9,00 ⋅ 0,017 = 1,741 tys. km

f) Odchylenie standardowe przebiegu między uszkodzeniami wyznaczymy zgodnie z wyrażeniem (4.59):

σ = (0,25² ⋅ 0,377 + 0,75² ⋅ 0,150 + 1,25² ⋅ 0,106 + 1,75² ⋅ 0,067 + 2,25² ⋅ 0,050 + + 2,75² ⋅ 0,040 + 3,75²⋅ 0,033 + 4,25²⋅ 0,027 + 4,75²⋅ 0,027 + 5,50²⋅ 0,033 + + 7,00² ⋅ 0,033 + 9,00²⋅ 0,017 - 1,741²)^1/2 = 1,995 tys. km

g) Weryfikacja hipotezy o rozkładzie wykładniczym przebiegu między uszkodzeniami przeprowadzona zostanie zgodnie z metodyką przedstawioną w punkcie 4.5. Wyniki obliczeń zamieszczono w tabeli 4.3.

Tabela 4.3.

Lp.	li	ni	λ ⋅ li	exp(-λ⋅li)	pi	n ⋅ pi
1	0,5	113	0,287	0,7483	0,2517	75,5	18,63
2	1,0	45	0,574	0,5655	0,1828	54,8	1,75
3	1,5	32	0,868	0,4189	0,1466	44,0	3,27
4	2,0	20	1,149	0,3166	0,1023	30,7	3,72
5	2,5	15	1,436	0,2369	0,0797	23,9	3,31
6	3,0	12	1,723	0,1791	0,0578	17,3	1,62
7	3,5	12	2,010	0,1340	0,0451	13,5	0,17
8	4,0	10	2,298	0,1003	0,0337	10,1	0,00
9	4,5	8	2,585	0,0750	0,0253	7,6	0,02
10	5,0	8	2,872	0,0567	0,0183	5,6	1,03
11	6,0	10	3,446	0,0317	0,0250	7,5	0,83
12	8,0	10	4,595	0,0101	0,0216	6,5	1,88
13	10,0	5	5,744	0,0032	0,0069	2,1	4,00
suma		300	-	-	0,9968	299,1	40,23

Zakładamy, że przebieg samochodu między uszkodzeniami ma rozkład wykładniczy o dystrybuancie:

F(l) = 1 - exp (-λl)

gdzie . Wartość prawdopodobieństwa p_i (tabela 4.3) jest równa przyrostowi dystrybuanty rozkładu wykładniczego:

p_i = F(l_i) - F(l_i-1)

Wartości te określono przy pomocy tablic funkcji wykładniczej. Wartość parametru χ² wyznaczona zgodnie z (4.60) jest równa 40,2, a liczba stopni swobody - 11 ponieważ wyznaczono jeden parametr rozkładu prawdopodobieństwa na podstawie wyników doświadczenia.

Na podstawie analizy danych w tablicy rozkładu χ² można sformułować wniosek, że badana charakterystyka empiryczna nie może być opisywana rozkładem wykładniczym. Otrzymana w wyniku obliczeń wartość parametru χ² przy liczbie stopni swobody 11 jest zbyt duża. Na ten fakt ma przede wszystkim wpływ stwierdzona duża liczba uszkodzeń pojazdu w przedziale przebiegu od 0 do 500 km. Analizowany przebieg jest dobrze opisywany rozkładem Weibulla.

f(l)

f(l)

l

l

R(l)

F(l)

l

1/

0



1

0

1/

l

F(l)

0,632

---