Politechnika Częstochowska

Wydział Elektryczny

LABORATORIUM ZAKŁÓCEŃ W UKŁADACH ELEKTROENERGETYCZNYCH

Badanie składowych symetrycznych w niesymetrycznym układzie trójfazowym

Studia niestacjonarne II-go stopnia

Semestr I

Opracował: Tomasz Dróżdż

Tomasz Sekret

16.12.2011r

1. Cel ćwiczenia.

Celem ćwiczenia są pomiary składowych symetrycznych kolejności zgodnej i przeciwnej napięć międzyfazowych oraz porównanie wyników pomiarów z wynikami uzyskanymi sposobami analitycznymi i wykreślnymi.

2. Schemat pomiarowy i tabela pomiarów.

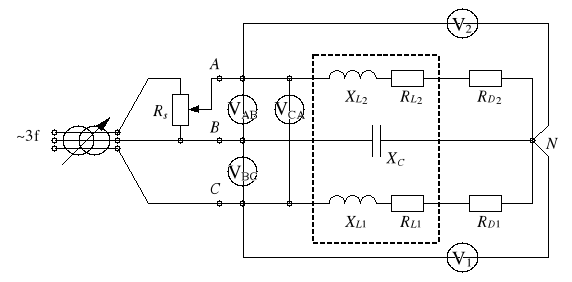
	Pomiary
		UAB	UBC	UCA	U1	U2
		V	V	V	V	V
1	51,0	55,0	54,0	2,18	53,3
2	24,0	55,0	44,0	14,0	42,6
3	0	55,0	54,0	27,4	38,3

3. Parametry i dane znamionowe zastosowanych przyrządów.

1. Autotransformator 400 / 60 V 50 Hz;

2. Opornica suwakowa;

3. Woltomierz MERA - 3 szt.;

4. Multimetr METEX MXD-4660A;

5. Opornica dekadowa DR6-16 - 2 szt.

4. Wyznaczenie zespolonych wartości napięć liniowych.

Z twierdzenia kosinusów:

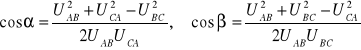
- pomiar 1: cos α = 0,48 ≈ 63°, cosβ = 0,0017 ≈ 89°

przyjmując, że kąt przesunięcia fazowego napięcia U_AB jest równy zero, otrzymujemy:

stąd otrzymujemy:

U_AB = 51 V, U_BC = 55 e ^-j121 U_CA = 54 e ^j119

- pomiar 2: cos α = -0,24 ≈ 76°, cosβ = 0,004 ≈ 88°

U_AB = 24 V, U_BC = 55 e ^-j121 U_CA = 44 e ^j121

- pomiar 3: cos α = 0 ≈ 90°, cosβ = 0 ≈ 90°

U_AB = 0V, U_BC = 55e ^-j121 U_CA = 27 e ^j121

5. Wyznaczenie składowych symetrycznych napięć liniowych metodą

analityczną.

gdzie: a = e ^j120 a² = e ^-j120

pomiar 1: U₁ = 51,63 - j2,076 = 51,67 V, U₂ = 0,833 + j1,943 = 2,11 V

pomiar 2: U₁ = 36,65 - j11,84 = 38,52 V, U₂ = - 10,23 + j11,17 = 15,15 V

pomiar 3: U₁ = 20,28 - j22,75 = 30,48 V, U₂ = - 18,55 + j22,66 = 29,28 V

6. Tabela wyników obliczeń.

Lp.	Pomiary					Metoda analityczna					Metoda wykreślna
		UAB	UBC	UCA	U1	U2	UAB	UBC	UCA	U1	U2	U1	U2
		V	V	V	V	V	V	V	V	V	V	V	V
1	51,0	55,0	54,0	2,18	53,3	52,5	53,0	52,5	51,6	2,11	51,6	2,0
2	24,0	55,0	44,0	14,0	42,6	26,2	52,5	41,6	38,5	15,5	40,4	14,8
3	0	55,0	54,0	27,4	38,3	5,6	52,5	53,0	30,4	29,2	31,2	28,0

7. Wnioski.

W układach trójkątnych i gwiazdowych napięcia liniowe nie zawierają składowej zerowej kolejności. Im bardziej układ jest niesymetryczny tym wartość skuteczna składowej kolejności przeciwnej jest większa co możemy potwierdzić na podstawie przeprowadzonego ćwiczenia. Wraz ze wzrostem asymetrii układu wzrastał wskaz składowej kolejności przeciwnej (U₂), malał natomiast wskaz składowej kolejności zgodnej. Tak więc składowa kolejności przeciwnej świadczy o stopniu asymetrii układu. Składową symetryczną układu trójfazowego można wyznaczyć także metodą graficzną.

Podczas wykonywania tego ćwiczenia zapoznaliśmy się z wpływem asymetrii układu na wartość składowych symetrycznych napięć przewodowych. Składowe symetryczne pozwalają na zastąpienie dowolnego układu trójfazowego napięć lub prądów zespołem trzech układów symetrycznych : kolejności zgodnej , przeciwnej oraz zerowej , a następnie zastosować dla nich superpozycję.

4

---