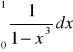
Egzamin z polibudy semestr II -3.

Zad 1. Zbieżność całki (ilorazowe, porównawcze, całkowe)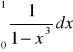

Zad 2. Zbieżność szeregu (całkowe, Alembert, Cauchy)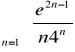

Zad 3. Suma szeregu potęgowego (częściowa)

Zad 4. Przedział szeregu potęgowego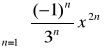

Zad 3. Dziedziny naturalne(poziomice) f(x,y)=ln

Zad 4. Granica (ciągłość) f(x,y) =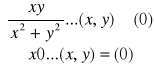

Zad 5. Extremum lokalne f(x,y) = (x²-2y)

funkcji uwikłanej (x-y)² -y -xy +3x =0

pod warunkiem f(x,y) =

Zad 6. Styczna do krzywej
P(x,0)

płaszczyzna (2,1,z₀) z = x^xy

Zad 7. Różniczka

Zad 8. Rozwinąć w szereg Maclaurina

Zad 9. Oblicz całkę niewłaściwą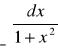

Zad 10. Pochodne kierunkowe
(3,-4) v =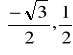

zad 11. Całki podwójne -pole płata -szkicowanie obszarów

-iteracja

-moment bezwładności

-moment statyczny

-masa układu

-objętość

-wartość średnia

Oblicz pole płata z =
x² + y ² =1

Oblicz V jeśli obszar całkowania wynosi x² + y² -2x,

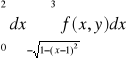
iteracja i obszar całkowania

Moment bezwładności x²+y²<4 x>0

D: y² = x x=3y
masa obszaru

D : x² -2x+ y² =0 z = 0 objętość

F(x,y) = (x²+ y²)^-1,5 D: x² +y ² =2 x>1 y>0 wartość średnia