Otrzymujemy tu osłabienie fazy (patrz rys. 3) lub nawet całkowite jej wygaszenie, gdy E₀₁ = E₀₂. W tym ostatnim przypadku światło nie rozchodzi się w ośrodku (rys. 4).

W pozostałych przypadkach mamy do czynienia z różnymi stopniami wzmocnienia lub osłabienia się fal.

§3. POLARYZACJA ŚWIATŁA

Z innymi jednak efektami spotykamy się, gdy nakładać się będą na siebie fale, w których kierunki drgań wektora elektrycznego nie są jednakowe.

Bez ograniczenia ogólności rozważań możemy przyjąć, że kierunki drgań wektora elektrycznego w obu falach są do siebie prostopadłe. Istotnie, w przeciwnym przypadku każdą z fal moglibyśmy rozłożyć na dwie składowe Y i Z, w których drgania odbywają się wzdłuż dwu nawzajem prostopadłych osi Y i Z. W wyniki interferencji składowych Y obu fal otrzymamy fale, w której drgania odbywają się wzdłuż osi Y. Analogiczna sytuacja zachodzi dla składowych Z. W ten sposób możemy zastąpić
każdą parę spolaryzowanych liniowo fal, których płaszczyzny polaryzacji tworzą ze sobą kąt różny od zera, przez parę fal spolaryzowanych w płaszczyznach wzajemnie prostopadłych.

Niech fale składowe będą postaci

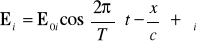
dla i = 1, 2, (18)

gdzie wektory

, (19)

. (20)

W wyniku nałożenia obu tych fal drgania wektora elektrycznego opisane będą przez równanie

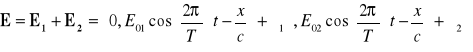
. (21)

W przypadkach, gdy δ₁ = δ₂ = δ lub δ₁ = δ₂ + 180˚ = δ równanie (21) możemy zapisać w prostszej postaci

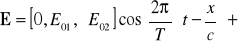
. (22)

Kierunek drgań wektora elektrycznego [0,E₀₁,±E₀₂] w obu tych przypadkach jest stały, co oznacza, że światło pozostaje liniowo spolaryzowane.

W pozostałych przypadkach koniec wektora elektrycznego zakreśla w płaszczyźnie YZ elipsę. Mówimy wówczas, że światło jest spolaryzowane eliptycznie (rys. 5).

STOP

I=1(1)X

WARTOŚĆ A

A=SQR(X^3)

PODAJ X

START

B=EXP(EX)

B<5

B=B*5

B=B*1

N

T

I=X

1

2

1

2

Rys. 4. Wygaszanie się dwu fal o tych samych okresach i amplitudach, a fazach różniących się o 180˚.

x

E

Z

Y

Y

Z

E

E

Rys. 5. Drgania wektora elektrycznego światła spolaryzowanego eliptycznie

Rys. 6. Drgania wektora elektrycznego światła spolaryzowanego kołowo

---