1. Opis ćwiczenia

Celem naszego ćwiczenia była obserwacja zjawiska dyfrakcji elektronów oraz wyznaczenie odległości między płaszczyznowych w graficie. W tym celu posłużyliśmy się następującą aparaturą.

W szklanej lampie próżniowej znajdują się

1. K - katoda (źródło elektronów)

2. H - cylinder Wehnelta (regulacja natężenia wiązki elektronów)

3. G - elektrody ogniskujące wiązkę

4. A - anoda

5. P - grafit polikrystaliczny

6. E - ekran pokryty luminoforem

2. Przebieg ćwiczenia

Po odpowiednim uruchomieniu aparatury ustawiliśmy napięcie anodowe na wartość 4 kV a następnie napięcie ogniskujące ustawiliśmy tak by okręgi na ekranie były wyraźne, ale niezbyt jaskrawe. Po Ustawieniu aparatury dokonaliśmy pomiarów średnic dwóch okręgów, które zaobserwowaliśmy. Kolejnych pomiarów średnic dokonywaliśmy zmieniając napięcie anodowe co 0,5kV aż do wartości 9kV. Uzyskane wartości przedstawiliśmy w poniższej tabeli

3. Wyniki pomiarów i obliczenia:

Tabela z wynikami pomiarów

lp	UA [1V]	D1 [1mm]	D2 [1mm]
1	4000	26	44
2	4500	24	42
3	5000	22	38
4	5500	20	36
5	6000	20	36
6	6500	20	34
7	7000	20	32
8	7500	20	30
9	8000	18	30
10	8500	18	30
11	9000	18	28

Aby obliczyć sin4 zastosowaliśmy następujący wzór:

Gdzie: D - jest średnicą mierzonego pierścienia, R - jest promieniem lampy i wynosi 65mm

Następnie by obliczyć kąt  posłużyliśmy się wzorem:

Po obliczeniu konta  policzyliśmy wartości sin i zamieściliśmy wyniki w tabeli poniżej

	Sin4		Sin		Kąt  [1°]
lp	Pierścienie małe	Pierścienie durze	Pierścienie małe	Pierścienie duże	Pierścienie małe	Pierścienie duże
1	0,200	0,338	0,050	0,087	3,204	5,487
2	0,185	0,323	0,045	0,081	2,961	5,234
3	0,169	0,292	0,043	0,073	2,702	4,716
4	0,154	0,277	0,038	0,071	2,460	4,467
5	0,154	0,277	0,038	0,071	2,460	4,467
6	0,154	0,262	0,038	0,066	2,460	4,219
7	0,154	0,246	0,038	0,063	2,460	3,956
8	0,154	0,231	0,038	0,058	2,460	3,710
9	0,138	0,231	0,035	0,058	2,203	3,710
10	0,138	0,231	0,035	0,058	2,203	3,710
11	0,138	0,215	0,035	0,055	2,203	3,449

Posiadając wartości sin i U_A stosując metodę najmniejszych kwadratów obliczyliśmy współczynnik nachylenia prostych funkcji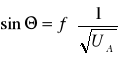
:

Dla małych pierścieni :

a = 2.567

Δa=0,323

Dla dużych pierścieni :

a = 5,908

Δa=0,310

Następnie obliczyliśmy odległości międzypłaszczyznowe d₁ i d₂ stosując wzór:

Gdzie :

h - stała Plancka

m - masa spoczynkowa elektronu

e - ładunek elektronu

Po podstawieniu wartości do powyższego wzoru otrzymaliśmy:

Dla małych pierścieni d₁ = 238,812
m

Dla dużych pierścieni d₂ = 103,771
m

Stosując metodę różniczki zupełnej obliczyliśmy błąd wielkości d₁ i d₂

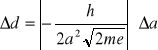
Otrzymaliśmy:

Dla małych pierścieni d₁ =30
m

Dla dużych pierścieni d₂ = 5,45
m

Ostateczne wyniki:

Małe pierścienie: d₁ = (238,81 ± 30)pm

Duże pierścienie: d₂ =(103,771 ± 5,45)pm

4. Wnioski:

1. wraz ze zmianą napięcia anodowego U_A zmieniają się średnice obserwowanych pierścieni (im większe napięcie tym mniejsza średnica)

2. także ze zwiększaniem napięcia anodowego U_A pierścienie stawały się wyraźniejsze

3. długość średnic pierścieni zależy od odległości międzypłaszczyznowej materiału przez który przepuszczana jest wiązka elektronów( w tym przypadku był to grafit)

4. porównując otrzymane wyniki z wymiarami przedstawionymi na rysunkiem dołączonym do instrukcji uważamy że zastosowana metoda jest dość dokładna, a zaistniałe różnice wynikły z trudności pomiaru.

3

---