***
94.04.11
Tomasz Skrobacz
ćwiczenie nr 46
Wyznaczanie stałej siatki dyfrakcyjnej
Laboratorium z fizyki
SIATKA DYFRAKCYJNA
Siatka dyfrakcyjna - przyrząd do widomej analizy oraz pomiarów długości fali światła; jest to przeźroczysta płytka lub zwierciadło metaliczne, na których nacięto gęsto równoległe i równoodległe rysy; powstałe między rysami szczeliny powodują uginanie przechodzących lub odbitych wiązek światła, które zebrane przez soczewkę inteferują na ekranie, dając widmo dyfrakcyjne.
Odstęp między szczelinami siatki dyfrakcyjnej (stała siatki) d dla typowych siatek zawierających 12000 szczelin na 2,54 cm szerokości siatki wynosi 2,54cm/12000 ;czyli 21000 A.
Siatki dyfrakcyjne używane są do pomiarów długości fali i do badań struktury i natężenia linii widmowych.
Siatki dyfrakcyjne robi się przez nacinanie równoległych, równoodległych rowków na szkle lub metalowej płycie za pomocą diamentowego ostrza, których ruch jest kierowany przez skomplikowaną maszynę kreślarską. Sporządziwszy taką wzorcową siatkę dyfrakcyjną, można robić następnie siatki pokrywając je roztworem kolodium, a następnie zdejmując stwardniałą warstwę nałożyć na płytkę szklaną.
Instrumenty z siatkami dyfrakcyjnymi mogą być użyte do absolutnych pomiarów długości fali, gdyż stałą d można dokładnie zmierzyć pod mikroskopem.
ZJAWISKO DYFRAKCJI - WARUNKI POWSTANIA
DYFRAKCJA jest to zjawisko polegające na uginaniu się promieni świetlnych przechodzących w pobliżu przeszkody, takiej jak np. brzeg szczeliny.
Dyfrakcje światła możemy zaobserwować patrząc przez szparkę między dwoma palcami na odległe źródła światła.
INTERFERENCJA FAL
Wzajemne nakładanie się fal o tej samej częstotliwości w danym ośrodku, prowadzące do wzmocnienia lub osłabienia (w zależności od różnicy faz fal składowych) natężenia fali wypadkowej.
Ćwiczenie polega na wyznaczeniu stałej siatki dyfrakcyjnej tj. odległości między dwiema sąsiednimi szczelinami lub przesłonami. Wielkość tę oznaczamy d. Jeżeli różnica dróg optycznych dwu sąsiednich ugiętych promieni /wiązek / światła równa będzie całkowitej wielokrotności długości fali padającego światła - nakładające się wiązki ulegną wzmocnieniu. Warunkiem wzmocnienia jest d sina = n l
l - długość fali, n - 0, 1, 2, 3, 4, ...
Zakładamy, że na siatkę pada fala płaska /co spełnia w przybliżeniu wiązka równoległa/ światła monochromatycznego, które po przejściu przez siatkę ulega ugięciu. Ugięte fale pochodzące od sąsiednich szczelin nakładają się i jeżeli spełniony jest warunek omówiony wyżej powstaje wzmocniony obraz /jasny/ ugiętej fali. To zachowanie się światła można przedstawić na rysunku:
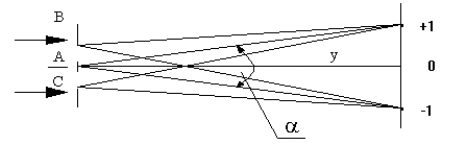
0 - miejsce prążka zerowego, gdzie różnica dróg optycznych dla obu promieni wynosi 0 /równoważne warunkowi n=0/. +,+1, -1 najbliższe miejsca jasne /prążki pierwszego rzędu /.
W miejscach oznaczonych +1 i -1 wiązki światła spełniają zależność:
d sina= l. a - jest to kąt pod jakim z punktu A widać odległość x pomiędzy prążkiem zerowym a prążkiem ugiętym /pierwszym/. Przyjmując, że stała d jest niewielka w stosunku do x oraz y otrzymuje się warunek wzmocnienia obrazu interferencyjnego w postaci:
![]()
skąd po przekształceniu: ![]()
Jest to wzór określający stałą siatki.
Wykonanie ćwiczenia:
Przyrządy: ława optyczna, źródło światła monochromatycznego /lampa sodowa/, przesłona, układ soczewek, siatka dyfrakcyjna w uchwycie, półprzeźroczysty ekran z podziałką milimetrową.
Kolejność czynności:
1. Zestawić układ optyczny według rysunku:

2. Wsunąć siatkę dyfrakcyjną. Włączyć lampę sodową / l = 590 nm. / Poczekać /ok. 5 minut /, aż lampa będzie świecić intensywnym żółtym światłem.
UWAGA! W przypadku wyłączenia lampy powtórny zapłon możliwy jest dopiero po wystygnięciu lampy.
3. Ustawić soczewkę / S / tak, aby na ekranie E pojawił się ostry i dobrze widoczny obraz szczeliny.
4. Ustawić siatkę dyfrakcyjną jak najbliżej soczewki. Obserwować widoczne na ekranie prążki powstałe symetrycznie po obu stronach obrazu szczeliny.
5. Zmierzyć odległość między soczewką a ekranem - y oraz odległość między zerowym a pierwszym prążkiem - x.
6. Pomiary powtórzyć kilka razy. Zwrócić uwagę na dokładność określenia Dx. Aby oszacować Dy należy podczas jednego z pomiarów przesówać ekran wzdłuż ławy optycznej w prawo i w lewo od położenia pierwotnego do zauważenia zmiany ostrości obrazu. Połowę przesunięcia przyjąć za Dy.
Wyniki pomiarów umieścić w tabelce:
Obliczamy sina korzystając z własności trygonometrycznych w trójkącie prostokątnym oraz prawa Pitagorasa.
Otrzymujemy ostatecznie :
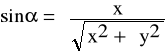
Stałą siatki obliczamy korzystając ze wzoru :
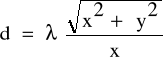
Dyskusja błędów :
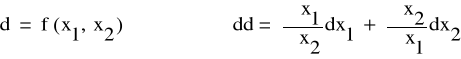
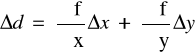
Obliczamy pochodną po x :
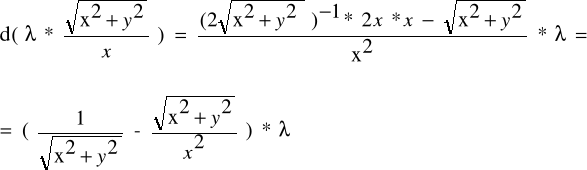
Obliczamy pochodną po y :
Obliczamy końcowy błąd Dd :
Wyszukiwarka