PRZESTRZENIE UNITARNE

1. ILOCZYN SKALARNY

1.1. DEFINICJA. Niech V będzie przestrzenią wektorową nad ciałem K. Funkcję nazywamy iloczynem skalarnym na V , jeśli spełnia ona następujące warunki :

i) ,

ii) , dla dowolnych v, u, u₁, u₂ ∈ V , a_1, a₂ ∈ K, oraz

iii) g(v,v) ≥ 0 dla dowolnego v ∈ V i równość zachodzi ⇔ v =0.

Iloczyn skalarny oznaczamy symbolem <⋅,⋅〉 , tzn. zamiast g(u,v) piszemy <u,v〉.

UWAGA. Jeśli K = R, to ii) oznacza symetrię g(v,u) = g(u,v) dla u,v ∈ V.

FAKT. Niech <⋅,⋅〉 będzie iloczynem skalarnym na przestrzeni wektorowej V. Wtedy

1. <u,v₁ + v_­­2〉 = <u,v₁ 〉 + <u, v_­­2〉.

2.

2. 
   

1.2. DEFINICJA. Niech <⋅,⋅〉 będzie iloczynem skalarnym na przestrzeni wektorowej V i (v₁,...,v_m) układ wektorów w przestrzeni V. Wtedy m×m macierz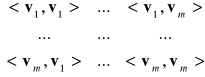

nazywamy macierzą Grama układu (v₁,...,v_m) względem <⋅,⋅〉 i oznaczamy M_G(v₁,...,v_m). Wyznacznik tej macierzy nazywamy wyznacznikiem Grama układu (v₁,...,v_m) względem <⋅,⋅〉 i oznaczamy Γ(v₁,...,v_m). Jeśli B = (v₁,...,v_n) jest bazą V , to macierz Grama M_G(B) nazywamy macierzą <⋅,⋅〉 w bazie B.

TWIERDZENIE. Niech <⋅,⋅〉 będzie iloczynem skalarnym na przestrzeni wektorowej V nad K i niech B = (v₁,...,v_n) będzie bazą V. Ponadto, niech A = ∈ M_nⁿ(K). Wtedy następujące warunki są równoważne:

1. A = M_G(B)

1. < u,v 〉 = .

1.3. TWIERDZENIE. Niech <⋅,⋅〉 będzie iloczynem skalarnym na przestrzeni wektorowej V. Wtedy Γ(v₁,...,v_m) > 0 dla każdego liniowo niezależnego układu (v₁,...,v_m) wektorów z V oraz Γ(v₁,...,v_m) = 0 dla każdego liniowo zależnego układu (v₁,...,v_m) wektorów z V.

1.4. DEFINICJA. Przestrzenią unitarną nad ciałem K nazywamy parę (V, <⋅,⋅〉), gdzie V jest przestrzenią wektorową nad K, a <⋅,⋅〉 jest iloczynem skalarnym na V.

2.ORTOGONALNOŚĆ.

2.1.DEFINICJA. Niech <⋅,⋅〉 będzie iloczynem skalarnym na przestrzeni wektorowej V. Dwa wektory u, v z przestrzeni V nazywamy ortogonalnymi, jeśli <u,v〉= 0. Piszemy wtedy u ⊥ v. Dwa podzbiory A, B ⊆ V nazywamy ortogonalnymi , jeśli u ⊥ v dla dowolnych wektorów u ∈ A i v ∈ B. Piszemy wtedy A ⊥ B. Zbiór A^⊥ := {v ∈ V : {v} ⊥ A} nazywamy dopełnieniem ortogonalnym zbioru A.

TWIERDZENIE. Niech <⋅,⋅〉 będzie iloczynem skalarnym na przestrzeni wektorowej V i niech A i B będą podzbiorami V. Wtedy:

1. A ⊥ B wtedy i tylko wtedy, gdy B ⊥ A.

1. Jeśli A ⊥ B i C ⊆ A , to C ⊥ B.

2. A ⊥ B wtedy i tylko wtedy, gdy A ⊆ B ^⊥.

3. Jeśli A ⊆ B, to B ^⊥ ⊆ A ^⊥.

4. A ⊥ B wtedy i tylko wtedy, gdy L(A) ⊥ L(B).

5. A ^⊥ = L(A ^⊥) = (L(A)) ^⊥. W szczególności A ^⊥ jest podprzestrzenią przestrzeni V.

LEMAT. Niech <⋅,⋅〉 będzie iloczynem skalarnym na przestrzeni wektorowej V oraz niech v, u₁, ..., u_k będą wektorami z V. Wtedy, jeśli v ⊥ L(u₁, ... , u_k), to

Γ (v, u₁, ..., u_k) = <v,v> Γ(u₁, ..., u_k).

2.2. DEFINICJA. Niech <⋅,⋅〉 będzie iloczynem skalarnym na przestrzeni wektorowej V i niech U będzie podprzestrzenią V. Jeśli V = U ⊕ U^⊥, to rzut przestrzeni V na podprzestrzeń U wzdłuż U^⊥ nazywamy rzutem ortogonalnym V na U i oznaczamy P_U .

TWIERDZENIE. Niech <⋅,⋅〉 będzie iloczynem skalarnym na przestrzeni wektorowej V i niech U = L(u₁,..., u_k), gdzie wektory u₁,..., u_k są liniowo niezależnymi wektorami z V. Wtedy 1. V = U ⊕ U^⊥,

2. Dla dowolnego wektora v ∈ V , P_U(v) = x₁u₁ + ... +x_ku_k, gdzie liczby x₁, ..., x_k są rozwiązaniem następującego układu równań:

x₁ < u₁,u₁〉 + ... + x_k< u_k,u₁〉 = < v,u₁〉

....................................................

x₁< u₁,u_k 〉 + ... + x_k< u_k,u_k 〉= < v,u_k 〉 .

2.3.DEFINICJA. Układ wektorów (e₁,...,e_m) nazywamy układem ortonormalnym jeśli (e₁,...,e_m) jest układem ortogonalnym oraz <e_j,e_j〉 = 1, dla j = 1,..., m. Bazę przestrzeni V, która jest układem ortonormalnym nazywamy bazą ortonormalną.

TWIERDZENIE. Każda skończenie wymiarowa przestrzeń unitarna ma ortonormalną bazę.

TWIERDZENIE. Niech V będzie przestrzenią wektorową nad ciałem K a B = (v₁,...,v_n) będzie bazą przestrzeni V. Wtedy <u,v〉 = wtedy i tylko wtedy, gdy B jest bazą ortonormalną.

UWAGA. Jeśli układ wektorów B = (e₁,...,e_n) jest ortonormalną bazą przestrzeni wektorowej V i M_B(u) = [x₁,...x_n]^T, to x_j = <u,e_j〉 dla j = 1,...,n.

TWIERDZENIE. Niech (e₁,...,e_m) będzie ortonormalnym układem wektorów w przestrzeni unitarnej V i niech U = L(e₁,...,e_m). Wtedy dla dowolnego wektora v z przestrzeni V

P_u(v) = <v,e₁〉e₁ + ...+ <v,e_m〉e_m.

2.4. TWIERDZENIE. Niech <⋅,⋅〉 będzie iloczynem skalarnym na przestrzeni wektorowej V i niech wektory u₁, ..., u_k ∈ V będą takie że Γ (u₁, ..., u_k) ≠ 0. Ponadto niech U = L( u₁, ..., u_k) i v ∈ V. Wtedy, jeśli v' = v − P_U(v), to

1. g(v',v') =
   

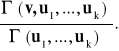
1. Γ(v', u₁, ..., u_k) = Γ(v, u₁, ..., u_k).

2. L(v, u₁, ..., u_k) = L(v, u₁, ..., u_k).

TWIERDZENIE. Niech <⋅,⋅〉 będzie iloczynem skalarnym na przestrzeni wektorowej V. Wtedy Γ(v₁,...,v_m) > 0 dla każdego liniowo niezależnego układu (v₁,...,v_m) wektorów z V.

2.5. TWIERDZENIE. Niech <⋅,⋅〉 będzie iloczynem skalarnym na przestrzeni wektorowej V i niech (v₁, ..., v_m) układ wektorów z V , taki że Γ(v₁, ..., v_k) ≠ 0 , dla k = 1, ..., m. Ponadto niech U_k = L(v₁, ..., v_k) i oznaczmy P_k = , dla k = 1, ..., m oraz u₁ = v₁, u_k = v_k − P_k(v_k), k = 2,...,m. Wtedy

1. Układ (u₁, ..., u_m) jest ortogonalny.

1. L(u₁, ..., u_k) = L(v₁, ..., v_k), dla k = 1, ..., m.

2. Γ(u₁, ..., u_k) = Γ(v₁, ..., v_k), dla k = 1,..., m.

3. u_k = v_k −
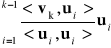
   , dla k = 2, ..., m. (***)

Proces otrzymywania układu ortogonalnego za pomocą rekurencyjnej reguły (***) nazywamy ortogonalizacją Grama-Schmidta.

3. OPERATORY NA PRZESTRZENIACH UNITARNYCH.

3.1. DEFINICJA. Operator liniowy F na przestrzeni unitarnej V nazywamy operatorem hermitowskim wtedy i tylko wtedy, gdy

(**) <F(u),v〉 = <u,F(v)〉,

dla dowolnych wektorów u,v ∈ V.

TWIERDZENIE. Niech F będzie operatorem liniowym na przestrzeni unitarnej V i niech B będzie ortonormalną bazą przestrzeni V. Wtedy F jest operatorem hermitowskim wtedy i tylko wtedy, gdy M^B_B(F) jest macierzą hermitowską.

3.2.TWIERDZENIE. Wartości własne operatorów hermitowskich na przestrzeniach unitarnych są liczbami rzeczywistymi.

LEMAT. Jeśli F jest operatorem hermitowskim na przestrzeni unitarnej V , to F ma niezerowy wektor własny.

TWIERDZENIE. Niech F będzie operatorem hermitowskim na przestrzeni unitarnej V i niech U będzie podprzestrzenią niezmienniczą względem F. Wtedy jeśli w ⊥ U, to F(w) ⊥ U , dla dowolnego wektora w z przestrzeni V (tzn.. podprzestrzeń U^⊥ jest podprzestrzenią niezmienniczą względem F).

WNIOSEK. Dopełnienie ortogonalne podprzestrzeni własnej operatora hermitowskiego jest podprzestrzenią niezmienniczą.

3.3. TWIERDZENIE (Spektralne dla operatorów hermitowskich) Niech V będzie skończenie wymiarową przestrzenią unitarną nad ciałem K i niech F będzie operatorem hermitowskim na przestrzeni V. Wtedy istnieje ortonormalna baza przestrzeni V złożona z wektorów własnych operatora F. (w szczególności oznacza to, że operatory hermitowskie są diagonalizowalne).

Bazę ortonormalną złożoną z wektorów własnych operatora hermitowskiego F nazywamy bazą spektralna dla operatora F.

UWAGA. Wektory własne operatora hermitowskiego odpowiadające różnym wartościom własnym są ortogonalne.

WNIOSEK. Jeśli macierz A jest macierzą hermitowską to istnieje macierz U spełniająca warunek U*U = I, taka że U*AU jest macierzą diagonalną.

DEFINICJA. Macierz kwadratową U spełniającą warunek U^-1 = U* (⇔ U*U = I) nazywamy macierzą unitarną. Jeśli macierz unitarna U jest macierzą o współczynnikach rzeczywistych, to nazywamy ją macierzą ortogonalną. Warunek U^-1 = U* przyjmuje wtedy postać U^-1 = U^T.

5

---