KINEMAYKA I DYNAMIKA
Zasada niezależności -Jeśli punkt materialny bierze udział jednocześnie udział w kilku ruchach (ruch złożony) to każdy z tych ruchów (składowych) odbywa się bez zakłóceń tak, jakby pozostałych ruchów nie było. W ruchu złożonym obowiązują następujące zależności - prędkość V ruchu złożonego jest wypadkową prędkości V1, V2...... ruchów składowych V=V1+V2+ ......
- przyśpieszenia a ruchu złożonego jest wypadkową przyśpieszeń a1, a2, .. ruchów składowych a=a1+a2+... Ruch ciała - przez ruch ciała rozumiemy zmianę jego położenia w stosunku do innych ciał, które uważamy za nieruchome.
Ruch krzywoliniowy- może być płaski lub przestrzenny. Przykładem ruchu płaskiego jest ruch po elipsie, po paraboli, po okręgu. Natomiast ruchu przestrzennego, ruch po linii śrubowej.
Δr=r2-r1 r=xi+yj - płaski
Δt=t2-t1 r=xi+yj+zk - przestrzenny
Wektor prędkości średniej jest zgodny co do kierunku z ΔV
Vśr=Δv/Δt Δt→0
Wtedy otrzymujemy prędkość chwilową wektorową w punkcie A ![]()
Wartość liczbowa wektora V
![]()
Kierunek wektora prędkości chwilowej jest styczny do toru wdanym punkcie.
![]()
Przedstawienie wektora prędkości V za pomocą składowych skierowanych wzdłuż osi współrzędnych.
Przyspieszenie![]()
RUCH OBROTOWY-to taki ruch w którym wszystkie punkty ciała zataczają okręgi prostopadłe do osi obrotu przechodzących przez środki tych okręgów.
x = cosφ y = sinφ φ = φ(t)
Kąt φ można traktować jako tzw. drogę kątową promienia wodzącego. Charakter zależności drogi kątowej od czasu decyduje o tym czy ruch po okręgu jest jednostajny czy zmienny.
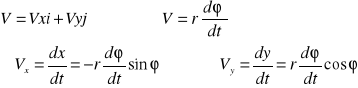
Pochodną drogi kątowej względem czasu dφ/dt nazywamy prędkością kątową ω V=ωr. Prędkość kątową umówiono się traktować jako wektor prostopadły do płaszczyzny toru kołowego, wyprowadzony z jego środka. Kierunek tego wektora określa reguła korkociągu. W ruchu jednostajnym φ=ωt x=r cosωt y=r sinωt
Vx=-ωr sinωt Vy=ωr cosωt V=ωr=2Πr/T
a=ω2r
W ruchu jednostajnym po okręgu wektor prędkości kątowej jest stały co do wartości, jak i co do kierunku. Przyspieszenie kątowe (α) ![]()
W ruchu niejednostajnym ω≠const. ![]()
a = axi+ayj ax=α/ω vx-ω2x ay=α/ω vy-ω2y
a=α/ω v-ω2r
ZASADY DYNAMIKI NEWTONA.
(układy inercjalne i nieinercjalne)
Układy inercjalne - nazywamy układy odniesienia w których spełnione są zasady dynamiki Newtona.
Układy nieinercjalne - nazywamy układy odniesienia w których działają tzw. siły bezwładności.
I zasada dynamiki newtona (zasada bezwładności) jeżeli na ciało nie działają żadne siły zewnętrzne lub działające siły równoważą się to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
II zasada dynamiki newtona
Jeżeli na ciało działa stała niezrównoważona siła zewnętrzna to względem inercjalnego układu odniesienia porusza się ono ruchem jednostajnie zmiennym z przyspieszeniem wprost proporcjonalnym do działającej siły, a odwrotnie proporcjonalnym do masy ciała. ![]()
III zasada dynamiki newtona
Jeżeli ciało A działa na ciało B siłą FAB to ciało B działa na ciało A siłą FBA równą co do wartości lecz przeciwnie skierowaną. FAB= -FBA
ZASADA d'ALEMBERTA
Ciało spoczywa w układzie nieinercjalnym, gdy suma wszystkich sił działających, łącznie z siłą bezwładności, równa się zero.
Siła bezwładności F0= - maμ jest równa iloczynowi masy ciała przez przyspieszenie ciała aμ
Rozpatrując ruch ciała z punktu widzenia obserwatora znajdującego się w układzie nieinercjalnym tzn. poruszającym ruchem zmiennym względem układu inercjalnego, musimy do siły F1 działającej na ciało w układzie inercjalnym dodawać siłę F0 równa liczbowo iloczynowi masy ciała przez przyspieszenie aμ układu, lecz skierowana przeciwnie względem przyspieszenia układu F2=F1+F0
siła coriolisa Fc=2mVω
Siła ta ma kierunek prostopadły zarówno do prędkości V jak i do ω
ac=2(V×ω)
Fc=2m (V×ω)
ŚRODEK MASY
Środek masy układu n punktów materialnych o masach m1, m2,.....mn jest punktem którego współrzędne xo,yo, zo wyznacza się: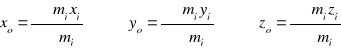
Ruch postępowy ciała złożonego z szeregu punktów materialnych o łącznej masie mo
moxo= m1x1+m2x2+... x0, x1, x2-jest funkcją mas.
Środek masy ciała ma tę właściwość, że iloczyn całkowitej masy mo i przyśpieszenia środka masy ao równa się sumie geometrycznej wszystkich sił działających na poszczególne punkty układu. Siły te można podzielić na siły zewnętrzne Fz i wewnętrzne Fw ![]()
![]()
gdyż suma wypadkowa wszystkich sił wewnętrznych równa się zero, ponieważ występujące parami których składniki są równe co do wartości, lecz przeciwnie skierowane.
ZASADA ZACHOWANIA PĘDU.
Jeżeli na ciało lub na układ ciał nie działa żadna niezrównoważona siła zewnętrzna to ciało lub układ nie zmienia swojego pędu. p=mV
ZASADA ZACHOW. ENERGI MECHANICZNEJ jeżeli na ciało nie działa żadna siła zewnętrzna oprócz siły ciężkości to ciało nie zmienia swojej energii mechanicznej E=Ek+Ep=const
MECHANIKA BRYŁY SZTYWNEJ
Ciało którym nie zmienia się odległość dwóch dowolnie wybranych punktów mimo działania sił zewnętrznych nazywamy bryłą sztywną. Ciało sztywne wykonuje ruch postępowy jeżeli odcinek łączący dwa dowolne punkty tego ciała pozostaje równoległy do toru ruchu.
RUCH DRGAJĄCY. PROSTY HARMONICZNY
Jest to ruch drgający ciała w którym wychylenie ciała od położenia równowagi jest wprost proporcjonalne do działającej siły. Warunek ruchu harmonicznego. F=-kx k=mω2 k-współ. Sprężystości. 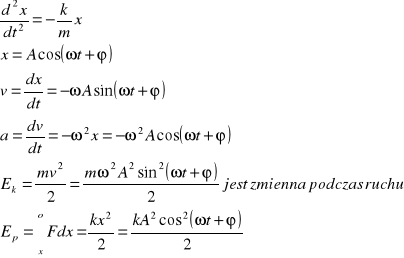
Ep= pracy którą ciało drgające może wykonać wracając od wychylenia do położenia równa się
Ec=Ek+Ep Ec=1/2mω2A2
RUCH HARMONICZNY TŁUMIONY
Drgania tłumione - są to drgania odbywane w warunkach rzeczywistych, które są połączone z przekazywaniem energii otoczeniu w związku z pokonywaniem sił oporu. W wyniku wykonywanej pracy energia ciała drgającego maleje, zmniejsza się też amplituda drgań.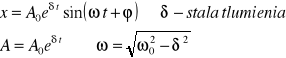
Drgania wymuszone - są to drgania powstające wtedy, gdy punkt drgający w ośrodku o stałej tłumienia δ poddany jest dodatkowo działaniu siły F sinusoidalnie zmiennej z biegiem czasu
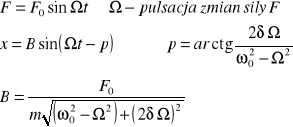
drgania wymuszone odbywają się z pulsacją Ω siły wymuszonej.
drgania wymuszone mają inną fazę niż siła wymuszająca.
Rezonans. Powstaje gdy pulsacja siły wymuszonej jest tak dobrana, że drgania wymuszone odbywają się z maksymalną amplitudą. ![]()
PODST. POJĘCIA RUCHU FALOWEGO.
Fale dzielimy na:
mechaniczne
elektromagnetyczne
głosowe
Istnienie fal mechanicznych związane jest ze zjawiskiem ruchu występującym w ośrodkach spreżystych istotą takiego ośrodka jest istnienie sił sprężystych wiążących cząstki z których są zbudowane. Wprowadzenie zaburzenia powoduje jego przechodzenie na kolejne sąsiadujące warstwy wprawiając je w ruch drgający.
Ruch falowy związany jest z dwoma procesami: z transportem energii przez ośrodek od cząsteczki do cząsteczki i z ruchem drgającym poszczególnych cząstek dokoła ich położenia równowagi.
Promień fali jest to każdy kierunek rozchodzenia się zaburzenia
Powierzchnia falowa jest to zbiór punktów ośrodka, w których zaburzenie ma tę samą fazę drgania w danej chwili.
Czoło fali jest to powierzchnia fali najdalej odsunięta od źródła.
Fala płaska jej promienie stanowią zbiór prostych równoległych
Fala poprzeczna -kierunek ruchu zaburzenia jest prostopadły do kierunku ruchu drgającego cząsteczki.
Fala podłużna -jest to fala której kierunek ruchu drgającego cząsteczek jest równoległy do kierunku ruchu zaburzenia.
Długość fali odległość między dwiema najbliższymi cząsteczkami ośrodka które mają jednakowe fazy drgań V=λ/T
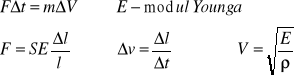
prędkość rozchodzenia się fali w pręcie zależy od modułu Younga i gęstości czyli wielkości charakteryzujące jego własności materiału a nie od przekroju czy wywołanego odkształcenia.
Energia i natężenie fali.
Natężenie fali jest to ilość energii przenoszonej w jednostce czasu przez jednostkę powierzchni ustawionej prostopadle do kierunku rozchodzenia się fali. W układzie SI natężenie fali wyraża się w W/m2
Natężenie fali I można powiązać z inną wielkością, a mianowicie z gęstością energii fali.
![]()
V-prędkość rozchodzenia się fali
ρ-gęstość ośrodka
Uo- amplituda prędkości ruchu harmonicznego
Interferencja jeżeli przez ośrodek sprężysty przechodzą dwie (lub kilka) fale pochodzące z różnych źródeł, to wychyleniu jakiemu podlega każda cząstka ośrodka będzie sumą wychyleń spowodowanych przez poszczególne fale. Oznacza to, że każda z cząstek drgających uczestniczy w kilku wzajemnie nakładających się ruchach, które mogą się osłabiać lub wzmacniać w zależności od tego czy odbywają się w fazach zgodnych czy przeciwnych. Zjawisko polegające na wzmacnianiu i osłabianiu drgań będących wynikiem nakładania się dwóch faz o jednakowych częstotliwościach i zgodnych fazach nazywamy interferencją fal.
Fale stojące. W przypadku interferencji dwóch fal o jednakowych amplitudach, częstościach i prędkościach rozchodzących się w przeciwnych kierunkach powstaje fala stojąca. Fale stojące może powstać również na wskutek interferencji fali.
KINETYCZNO MOLEKULARNA TEORIA GAZÓW. Teoria ta opiera się na następujących założeniach ogólnych:
Ciała mają budowę nieciągłą, składają się z drobnych cząsteczek w postaci atomów lub cząstek (molekułów)
Wymienione elementy budowy ciała są w ciągłym ruchu, wartości liczbowe i kinetyczne kierunki prędkości poszczególnych elementów są różne.
Pomiędzy poszczególnymi elementami budowy ciał występują siły wzajemnego oddziaływania.
Dla gazów: zakładamy, że każda cząsteczka porusza się swobodnie bez działania sił aż do momentu zderzenia z inną cząsteczką albo ścianką naczynia. Stąd wniosek, że odcinki dróg między kolejnymi zderzeniami są przebywane ruchem jednostajnym prostoliniowym. Wobec zupełnej przypadkowości zderzeń drogi te mają różne długości:
cząstki gazów na siebie nie działają aż do momentu zderzenia
rozmiary cząsteczek można pominąć, traktując je jako punkty. Cząsteczki podczas zderzeń zderzają swe prędkości. Zderzenie cząstek gazowych można traktować jako zderzenie doskonale sprężyste. Średnią długość ruchu prostoliniowego przebiegu między dwoma zderzeniami wyliczono z bardzo wielkiej liczby tych przelotów nosi nazwę średniej drogi swobodnej.
Kinetyczna interpretacja ciśnienia założenia dla interpretacji ciśnienia:
gaz jest zawarty w naczyniu kulistym o promieniu r
gaz jest tak zamknięty, że można brać pod uwagę tylko zderzenia za ściankami naczynia zaniedbując zderzenia międzycząsteczkowe.
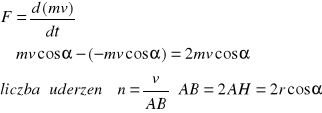
Zmiana pędu odpowiadająca n uderzeniom (w czasie 1s) będzie miarą siły oddziaływanie 1 cząsteczki na ściankę naczynia wyraża się wzorem F=2mvcosα=mv2/2
Kinetyczna interpretacja temperatury.
![]()
Zakładamy, że badana ilość gazu odpowiada 1 molowi.
V=Vm pVm=RT N=NA
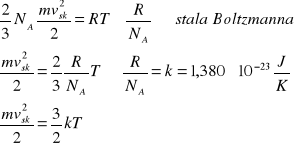
Średnia energia kinetyczna ruchu postępowego cząsteczek jest tylko funkcją temperatury bezwzględnej. Nie zależy od rodzaju gazu ani od jego ciśnienia. Temperatura jest wielkością statyczną. Zakładamy, że dwa różne gazy mają jednakową temperaturę, cząsteczki pierwszego gazu mają masę m1, a drugiego m2 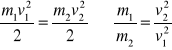
Gazy rzeczywiste i równanie van der Waalsa.
Dla gazów rzeczywistych przy ciśnieniach 106-107 N/m2 można stosować prawo Bogle`a-Mariotte`a ![]()
Równanie Bogle`a-Mariotte`a odnosi się do przemian izotermicznych określonej masy gazu.
T=const. To EKŚR=CONST N=const. Stąd pV=const.
Prawo Avogarda.
Mówi że w jednakowych objętościach różnych gazów mierzonych pod tym samym ciśnieniem i w tej samej temp. Znajduje się jednakowa liczba cząstek ![]()
![]()
Wobec równości p,V oraz średnich energii kinetycznych cząstek obu gazów. N1=N2
Całkowita energia wewnętrzna U gazu rzeczywistego nie równa się, jego energii kinetycznej, gdyż między cząsteczkowe, nieznaczne zresztą oddziaływania decydują o istnieniu energii potencjalnej Ep U=Ep+Ek
Wartość energii wewnętrznej gazu rzeczywistego zależy w dużym stopniu od zagęszczenia gazu.
Um=Em(energia molowa)
![]()
Równanie van der Waalsa
Van der Waals uwzględnił zaniedbane w przypadku gazu doskonałego.
siły między cząstkowe gazu
objętość własność cząstek gazu
Uwzględnienie sił spójności między cząsteczkami gazu sprowadza się do wyznaczenia poprawki na ciśnienie. Aby otrzymać wartość ciśnienia wewnętrznego, trzeba do ciśnienia zmierzonego dodać poprawę a/Vm2 chemiczna dla danego gazu
pVm=RT Vm-oznacza objętość naczynia zawierającego 1 mol gazu a-stała charakterystyczną dla danego gazu rzeczywistego.
Uwzględniając objętości własne cząsteczek musimy przyjąć, że objętość w której mogą się poruszać cząstki gazu, jest zmniejszona o pewną wartość zależną od objętości własnej cząsteczek. Druga poprawka b(stała dla danego gazu) powinna być czterokrotnej objętości własnej cząstek wchodzących w skład jednego mola.
Równanie van der Waalsa.
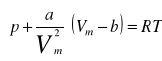
ZJAWISKO TRANSPORTU ENERGI, MASY I PĘDU
Zjawisko transportu czyli przenoszenie.
Transport energii - przewodnictwo cieplne
Przez przewodnictwo cieplne rozumiemy przenoszenie energii cieplnej wywołane istnieniem gradientu temperatury.
Różnica temperatury w różnych obszarach wiąże się z istnieniem różnic energii kinetycznych cząstek w tych obszarach. Ale z biegiem czasu na skutek nieuniknionych zderzeń międzycząsteczkowych odbywa się stopniowe wyrównywanie się średnich Ek a tym samym i temperatur. Każda z cząstek przenosi przez przekrój B tę ilość energii, którą uzyskała w czasie ostatniego zderzenia, które nastąpiło w odległości równej średniej drodze swobodnej l od przekroju B. Ponieważ gradient temperatury w obszarze między A i C równa się dT/dx, a więc różnica temperatur na odległości l wynosi (dT/dx)l, z tym że po prawej stronie od B mamy spadek temperatury równy (-dT/dx)l, po lewej stronie zaś wzrost równy (dT/dx)l. Jeżeli założymy, że przekrojowi B odpowiada temperatura T, to energię kinetyczną cząsteczki dochodzącej do B od lewej strony można wyrazić wzorem ![]()
a z prawej ![]()
m-masa cząsteczki
Oznaczając liczbę cząstek w jednostce objętości n, a ich prędkość średnią przez vŚR.. Wtedy energia przeniesiona w jednostce czasu przez jednostkową powierzchnię wyciętą z B wyrazi się wzorem: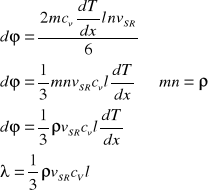
Transport masy - dyfuzja
Warunkiem wystąpienia procesu dyfuzji jest istnienie różnicy stężeń w różnych punktach obszaru zajmowanego przed dyfuzujące ciała
Gdyby cząsteczki gazów poruszały się bez zderzeń procesy dyfuzji zachodziły by bardzo szybko, tego jednak doświadczenia nie wykazują. Wskutek zderzeń międzycząsteczkowych każda cząstka gazu mimo, że przebiega w ciągu jednej sekundy drogę kilkuset metrów, to jednak ostatecznie w tym czasie mało się oddala od swego położenia początkowego. Im większa jest liczba zderzeń na sekundę, czyli im mniejsza jest średnia droga swobodna tym wolniej przebiega proces dyfuzji
Gęstość strumienia dyfuzji dφd=1/3(vśr)l(dc/dx)
D=1/3vśrl
Współczynnik dyfuzji jest proporcjonalny do średniej prędkości ruchu cieplnego gazu i do średniej drogi swobodnej
Transport pędu - lepkość
Niech laminarny przepływ gazu odbywa się w kierunku poziomym. W tych warunkach prędkość przepływu gazu w poszczególnych warstwach poziomych jest stała, zmienia się natomiast przy przejściu od warstwy do warstwy. Biorąc pod uwagę prędkość przepływu gazu w odległości średniej drogi swobodnej l po obu stronach c i uwzględniając fakt, że masy przenoszone w obu kierunkach przez jednostkową powierzchnie w jednostce czasu są jednakowe i równe 1/6 ρvśr to gęstość
strumienia pędu równa się:
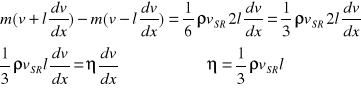
Współczynnika k lepkości gazów zależy od temperatury, gdyż vśr jest funkcją temp. Ze wzrostem temp. rośnie vśr i rośnie η
Równanie ciągłości strumienia masy ρ1v1s1=ρ2v2s2
Prawo Bernoulli'ego
Dotyczy przepływu cieczy doskonałej przez przewody o zmiennym przekroju. Wiąże ono ciśnienie i prędkość przepływów na poszczególnych przekrojach z powierzchniami tych przekrojów i ich wysokościami względem obranego poziomu odniesienia
p+ρgh+1/2(ρv2)=const
W przypadku szczególnym przepływu cieczy doskonałej przez przewód poziomy nie ma zmieny energii potencjalnej h=const więc p+1/2(ρv2)=const
Zastosowanie znalazło m.in. w pompie wodnej.
Zestawienie wielkości kinetycznych i dynamicznych w ruchu postępowym i obrotowym
Ruch postępowy Ruch obrotowy
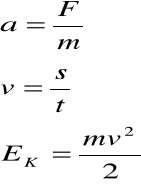
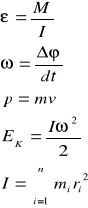
PODST. POJĘCIA TERMODYNAMICZNE
Układ termodynamiczny - zwany ciepłem roboczym np. gaz w zbiorniku zamknięty tłokiem.
Przemiana kołowa - stan początkowy i końcowy jest jednakowy
Przemiana otwarta - stan początkowy i końcowy jest różny ΔW=pSΔx=pΔV - rozprężanie gazu w cylindrze
Pracę uważamy za ujemną, jeżeli jest ona wykonana przez siły zewnętrzne na układzie, gdy układ wykonuje pracę dzięki działaniu sił wewnętrznych.
Jeżeli ΔQ=ΔW jest to tzw. obieg prosty (kosztem dostarczonego ciepła układ wykonuje pracę).
Jeżeli ΔQ i ΔW są ujemne jest to tzw. obieg odwrotny (kosztem dostarczonej pracy układ oddaje ciepło)
I zasada termodynamiki
W układzie zamkniętym, w którym zachodzą dowolne zjawiska mechaniczne, cieplne, elektryczne, magnetyczne, chemiczne lub przemiany jądrowe, nie można zmienić całkowitej energii układu U=const a więc ΔU=0
W układzie otwartym zmiana energii wewnętrznej tego układu ΔU może nastąpić albo pod wpływem ciepła Q lub pracy W ΔU=Q+W
Energia wewnętrzna układu U nazywamy sumę wszystkich rodzajów energii danego układu: energia kinetyczna cząstek układu, energii i oscylacji i rotacji cząstek, energii, wiązania, oddziaływań międzycząsteczkowych a nawet energii możliwych przemian jądrowych. Energia wewnętrzna jest to tzw. „funkcją stanu”, tzn. wielkością, której wartość określona jest jednoznacznie przez wartość parametrów stanu. Zmiany energii wewnętrznej są równe różnicy jej wartości w stanach końcowym 2 i początkowym 1 ΔU=U2-U1 Nie zależy ona od prowadzenia przemiany, czyli od drogi po której układ przeszedł od stanu 1 do 2
PRACA
Praca jest miarą zmiany energii. Praca wykonana nad doprowadzeniem układu do tego stanu(zmian energii) może być różna zależnie od sposobu jej wykonania, od drogi po której przebiega dany proces. Najczęściej spotykaną pracą jest praca objętościowa związana ze zmianą objętości układu. Jeżeli zmiana zachodzi przy stałym ciśnieniu zewnętrznym to praca W równa jest iloczynowi ciśnienia p przez zmianę objętości ΔV
W=-pΔV Ew> gdy V< stąd znak minus
CIEPŁO
Energia wewnętrzna zmienia się również, kiedy układ styka się z ciałem układem o innej temperaturze, wówczas następuje transport energii wewnętrznej z ciał układów o wyższej temperaturze do ciał układów o niższej temperaturze. Ten sposób wymiany energii wewnętrznej pod wpływem różnicy temperatur nazywa się ciepłem.
ENTROPIA
Entropię S definiuje się tak, że jej zmiana w procesie odwracalnym jest ilorazem ciepła Q przeniesionego w stałej temperaturze T i tej temperatury
![]()
Entropia jest dodatnia gdy ciału dostarczone jest ciepło(z otoczenia), entropia osiąga wartość max. w stanie równowagi
PROCESY ODWRAC. I NIEODWRACALNE
II ZASADA TERMODYNAMIKI
II zasada termodynamiki w jakimkolwiek procesie zachodzącym w układzie zamkniętym entropia nie może maleć. W procesach odwracalnych zmiana entropii jest równa stosunkowi ciepła Q do temperatury bezwzględnej To, a w procesach nieodwracalnych jest większa od tego stosunku.
Proces odwracalny jest to dowolny proces jeśli układ może go przebywać przechodząc przez te same stany zarówno w jednym jak i w drugim kierunku, przy czym po powrocie układu do stanu wyjściowego nie powstają żadne zmiany w otoczeniu układu (proces kołowy, ruch wahadła odbywający się bez tarcia)
Proces nieodwracalny są to wszystkie procesy rzeczywiste, tzn. nie dają żaden sposób cofnąć tak aby nie powstały jakieś zmiany w otoczeniu.
Wszystkie procesy zachodzące w przyrodzie samodzielnie przebiegają w jednym kierunku i są nieodwracalne.
Prawdopodobieństwo termodynamiczne - jest to liczba stanów mikroskopowych, które mogą realizować dany stan makroskopowy.
nazwę zjawiska fotoelektrycznego wewnętrznego tłumaczone jest w przejrzysty sposób pasmową teorią ciał stałych.
W temp. pokojowej pasmo walencyjne półprzewodników samoistnych jest praktycznie całkowicie zapełnione, zaś pasmo przewodnictwa puste. Padające promienie fotonu hν spełnia zależność
hν≥ΔE
ZJAWISKO COMPTONA
Polega na zmianie długości fali promieniowania rentgenowskiego przy zderzeniu się tego promieniowania z elektronem.
1
2
Wyszukiwarka