1. CELE ĆWICZENIA

Celem ćwiczenia jest sprawdzenie prawa Hook'a i wyznaczenie modułu Young'a przez pomiar wydłużenia drutu pod wpływem znanego obciążenia.

2. Wstęp teoretyczny

W fizyce niutonowskiej posługujemy się pojęciem punktu materialnego. Upraszcza to wiele zagadnień, tworząc matematyczny model zjawiska fizycznego. Nie należy jednak zapominać, że nawet najtwardsze materiały, takie jak diament czy widia (węglik żelaza) ulegają odkształceniom nawet pod działaniem stosunkowo niewielkich sił. Odkształcenia te mogą być nieznaczne (ciała stałe) lub większe (gazy, ciecze).

Ciało nazywamy sprężystym, jeżeli odkształcenia wywołane działającymi na nie siłami znikają zupełnie po ustąpieniu tych sił. Spójrzmy zatem na ten problem bardziej mikroskopowo. Istnienie równowagi trwałej między cząsteczkami ciała stałego (czyli węzłami sieci krystalicznej) wynika z faktu istnienia dwóch sił między cząsteczkami, odpychającej i przyciągającej i ich niejednakowej zależności od odległości między cząsteczkami. Przy czym siły odpychania rosną zawsze znacznie bardziej niż siły przyciągania. Dzięki temu przy pewnej odległości wzajamnej cząsteczek r0 siły te równoważą się, tworząc stan równowagi trwałej.

Siły przyciągania opisują następujące zależności:

, gdzie a,b zależą od budowy cząsteczki węzła sieci, a m jest zwykle rzędu 9, n zawiera sie w przedziale 2…7.

Duży wpływ na sprężystość ciał stałych ma również ich budowa, złożenie z wielu małych fragmentów kryształów.

Zadziałanie siłą osiową na pręt powoduje jego wydłużenie, a zarazem wzrost sił przyciągania między cząsteczkami poszczególnych warstw. Po przekroczeniu pewnej granicy cząsteczki nie powrócą już do poprzedniego stanu.

W rzeczywistości jednak proces odkształcania pręta w wyniku przemieszczania się cząsteczek nie przebiega tak prosto, jak by się to mogło wydawać. Towarzyszy mu również zmiana średnicy pręta.

Naprężeniem nazywamy wektor o wartości równej stosunkowi wartości siły do powierzchni, na którą ona działa, o kierunku i zwrocie zgodnym z kierunkiem siły:

Jednostką naprężenia jest Pascal [P], czyli takie naprężenie, jakie wywołuje jednostkowa siła działająca na jednostkę powierzchni.

Wyróżniamy zasadniczo 3 różne typy odkształceń, jakim ulegają ciałą:

odkształcenie jednostronne, l/l - odkształcenie względne,

odkształcenie wszechstronne, V/V - odkształcenie względne,

ścinanie, miarą jest kąt skręcenia ścianek 

Prawo Hooka formułuje zależność między naprężeniem, a odkształceniem. Jeżeli naprężenie w ciele jest dostatecznie małe, to wywołane przez nie odkształcenia względne są do nich wprost proporcjonalne.

Związek powyższy wyrażają wzory, których postać jest zależna od rozważanego odkształcenia, odpowiednio:

Współczynniki proporcjonalności 1/E, 1/K, 1/G nazywamy współczynnikami sprężystości, a ich odwrotności modułami odpowiednio: Younga, ściśliwości, sztywności. Są to stałe charakteryzujące dany rodzaj ciała, tzw. stałe materiałowe.

Wyprowadźmy zatem wzór, za pomocą którego będziemy obliczać wartość modułu Young 'a. Skorzystamy z prawa Hook 'a, wzoru na pole koła i definicji naprężenia:

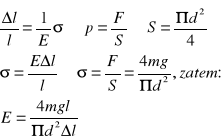
3. SPRAWDZENIE PRAWA HOOK 'A

Przed wykonaniem pomiarów mających na celu sprawdzenie prawa Hook'a i wyznaczenie modułu Young 'a badanego materiału - wyskalowaliśmy przyrządy pomiarowe. W tym celu zmierzyliśmy grubość wskaźników najpierw śrubą mikrometryczną, a potem w działkach mikroskopu.

To pozwoliło wyznaczyć z zależności w=q/q' wielkość działki przyrządu w milimetrach.

Średnia grubość wskaźnika gónego w milimetrach - 0,58mm ± 0,01,

a w dolnym 0,58m ± 0,01. Średnia grubość wskaźnika mikroskopu górnego w działkach mikroskopu - 2,2 a dolnego - 2,1. Po podstawieniu do w/w wzoru otrzymujemy, że w mikroskopie górnym wielkość działki wynosi 0,26 mm, a w dolnym 0,28 mm.

Sprawdzenie prawa Hook'a w tym ćwiczeniu polega na wykonaniu kilku pomiarów wydłużenia l stalowego drutu pod wpływem znanego obciążenia Q=mg i sporządzeniu wykresu l=f(Q).

Oto tabela otrzymanych wyników i wykres.

Q Odczyty na mikroskopach Wydłużenia l
[N] górny dolny góra dół [mm]
0 6.680 8.480 0 0 0
9.81 6.495 8.245 0.0481 0.0658 0.018
19.62 6.355 7.985 0.0845 0.1386 0.054
29.43 6.265 7.735 0.1079 0.2086 0.101
39.24 6.095 7.435 0.1521 0.2926 0.140
249.05 5.975 7.175 0.1833 0.3654 0.182
58.86 5.880 6.945 0.2080 0.4298 0.222

Błąd l obliczymy ze wzoru: (l )=w(a-b) = 0.02w ,ponieważ a=b=0.01

Tak więc w naszym przypadku (l )=0.006[mm]

Dołączony do sprawozdania wykres funkcji l=f(Q) na danym odcinku działających sił powinien być linią prostą. Jednak pomiar (1) i (2) obciążony jest błędem grubym. Dlatego wyznaczanie E przeprowadzę na podstawie pomiarów od 3 do 6, które w granicach błędu stosują się do prawa Hook 'a.

4. Wyznaczanie modułu Young 'a

Grubość drutu została zmierzona 10 razy w różnych miejscach i wynosi:

Nr pomiaru	Grubość [mm]	Średnia	Błąd d	Kwadraty błędów
1	0.89	0.892	0.002	4.00E-06
2	0.90		-0.008	6.40E-05
3	0.90		-0.008	6.40E-05
4	0.89		0.002	4.00E-06
5	0.89		0.002	4.00E-06
6	0.89		0.002	4.00E-06
7	0.89		0.002	4.00E-06
8	0.88		0.012	1.44E-04
9	0.89		0.002	4.00E-06
10	0.90		-0.008	6.40E-05
			Suma:	0.00036	Średni błąd kwadratowy:	0.002

Przy analizie błędu pomiaru d skorzystno z wyrażenia na średni błąd kwadratowy średniej:

Następnie zmierzyliśmy długość drutu za pomocą linijki, l=0,506 m ± 0,001 m

Obliczmy zatem E:

Należy teraz obliczyć błąd względny, stosując do wykorzystywanego wyżej wzoru metodę różniczki logarytmicznej.

Obliczymy teraz błąd bezwzględny otrzymanej wartości E:

5. Dyskusja BŁĘDÓW

W rachunku błędów czynniki o największym znaczeniu to przede wszystkim błąd pomiaru mikroskopem i błąd wyznaczania masy ciężarków. Na pewno duży wpływ na błąd pomiaru miała niestabilność układu pomiarowego. Na skutek skręcenia drutu przytwierdzone do niego wskaźniki odchylały się od płaszczyzny ostrości widzenia w mikroskopie, co powodowało duże problemy przy prowadzeniu odczytów. Aby poprawić dokładność wyznaczania modułu Young 'a w tym ćwiczeniu należałoby zadbać o takie prowadzenie drutu podczas pomiarów, aby nie było możliwości jego obrócenia. Niewątpliwie jakiś wpływ na błąd naszych obserwacji miała zmiana temperatury ( drut nagrzewał się od lamp podświetlających mikroskop ).Błąd ten możemy zaniedbać, ponieważ współczynnik rozszerzalności liniowej dla stali jest mały i wynosi: 0.000013 [1/K],a nasz pomiar i tak jest obciążony dużym błędem względnym ( 8.3% ).

6. Dyskusja WYNIKÓw i wnioski

Po porównaniu otrzymanego wyniku z odczytaną z tabeli wartością E dla stali ( wynosi ona
) stwierdzamy, że pomimo prostoty układu pomiarowego uzyskaliśmy wynik zgodny z danymi tablicowymi. Niemniej jednak duży błąd względny jak i duże uproszczenia przyjęte przy tej metodzie powodują, że nie można stosować jej np. przy zagadnieniach związanych z wytrzymałością materiałów. Najlepszym przykładem wielkości przyjętych uproszczeń jest fakt, że przy pomiarze założono stałość średnicy drutu. Na koniec warto dodać, że należałoby skrócić przymiar, tak aby można go było swobodnie przyłożyć do drutu i uniknąć błędu paralaksy.

---