3. Pole elektromagnetyczne w materii.

3.1. Równania Maxwella dla pola elektromagnetycznego

w materii .

Dotychczas rozpatrywaliśmy zachowanie się równań Maxwella w próżni. Materia zbudowana jest z atomów: dodatnio naładowanego jądra i krążących dookoła niego ujemnie naładowanych elektronów. Liczba ładunków jest bardzo duża, można więc wprowadzić podział na ładunki wewnętrzne i zewnętrze.

W rozdziale 2 wyprowadziliśmy równanie Coulomba:

gdzie ρ oznacza gęstość ładunku. Wprowadzając podział na ładunki wewnętrzne i zewnętrzne, gęstość ładunku zapisujemy jako:

(3.1)

Taki podział pozwala na zapisanie wektora polaryzacji:

(3.2)

oraz

(3.3)

W próżni równanie (3.3) przyjmowało postać :
. W materii pojawia się wektor polaryzacji:

Sumę wektorów
nazywamy wektorem polaryzacji.

Ładunki zewnętrzne
są ładunkami „swobodnymi”, ich wartość może ulegać zmianom (w zależności od proporcji ładunków swobodnych (-) i ładunków dodatnich, ciało może być naładowane dodatnio, ujemnie bądź obojętnie elektrycznie). Ładunki wewnętrzne
są ładunkami „związanymi”, oznacza to, że nie mogą „swobodnie” poruszać się wzdłuż ciała. Położenie ładunków może podlegać niewielkim wychyleniom od ich pierwotnego umiejscowienia. Ta właściwość ładunków wewnętrznych ma znaczny wpływ na zjawisko polaryzacji oraz wektora polaryzacji. W dielektrykach atomy uzyskują moment dipolowy, którego zwrot linii sił pola magnetycznego, działającego na to ciało. Wektor polaryzacji określa stopień polaryzacji dielektryka. Możemy go wyznaczyć badając wypadkowy moment dipolowy wszystkich cząstek.

W ośrodkach izotropowych, wektory
i
charakteryzują następujące zależności:

(3.4)

(3.5)

ε=1+ χ (w układzie SI) (3.6)

lub ε=1+4πχ (w układzie Gaussa) (3.7)

gdzie: ε - przenikalność elektryczna

χ - podatność elektryczna

Z równań Maxwella:

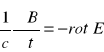
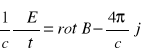
Podobnie jak w przypadku podziału ładunków na wewnętrzne i zewnętrzne, wprowadzamy podział na prąd zewnętrzny i prąd wewnętrzny:

(3.8)

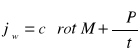
(3.9)

Moment dipolowy poszczególnych atomów oznaczaliśmy:

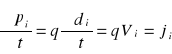
(3.10)

rozwijając (3.10):

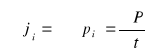
(3.11)

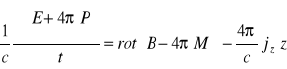
(3.12)

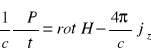
(3.13)

gdzie:

- momenty magnetyczne

3.2. Równania materialne. Makroskopowe równania

Maxwella.

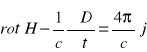
(3.14)

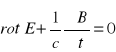
(3.15)

gdzie:

=indukcja elektryczna

=pole magnetyczne

=średnie momenty polaryzacji i magnetyczny

Ośrodek jednorodny izotropowy:

(prawo Ohma) (3.16)

(3.17)

(3.18)

(3.19)

(3.20)

Ośrodek nieizotropowy:

(3.21)

- tensor przenikalności elektrycznej

(3.22)

(3.23)

(3.24)

Cząsteczki dielektryków można rozpatrywać jako dwa przypadki: te które mają stały moment dipolowy (np. woda) oraz te które go nie mają (wynosi on zero). Pod wpływem zewnętrznego pola elektrycznego cząsteczki dipoli ustawiają się zgodnie z kierunkiem sił pola. Jest to cecha substancji polarnych. Inną własnością dielektryków, bez znaczenia na podział na ciała polarne i niepolarne, jest uzyskanie chwilowego momentu dipolowego (substancje polarne mają stały moment dipolowy) poprzez indukcję (wpływ). Indukowany moment dipolowy istnieje tylko w obecności pola elektrycznego i jest proporcjonalny do natężenia pola elektrycznego. Właściwości magnetyczne substancji można podzielić na trzy główne grupy:

- ferromagnetyki,

- paramagnetyki,

- diamagnetyki.

FERROMAGNETYKI. Wektor namagnesowania nie jest proporcjonalny do natężenia pola magnetycznego. Wzrost natężenia pola magnetycznego powoduje bardzo szybki wzrost namagnesowania ferromagnetyka, aż do pewnego momentu, nazywanego nasyceniem magnetycznym.

Cechą charakterystyczną ferromagnetyków jest to, że właściwości ferromagnetyczne występują tylko w stanie stałym. Uwarunkowane jest to krystaliczną budową struktury substancji oraz występowaniem domen. Domeny są obszarami, których momenty magnetyczne atomów ustawione są w tym samym kierunku. Przewaga jednego kierunku, mimo makroskopowej obojętności magnetycznej, nazywamy kierunkiem łatwego namagnesowania.

Własności domen przejawiają się tylko w pewnym zakresie temperatur, gdyż temperatura ma ogromny wpływ na energię cząstek, a zbyt duża energia niszczy „porządek” wśród domen. Każdy ferromagnetyk ma punkt granicznej temperatury, zwany punktem Curie, powyżej którego każdy ferromagnetyk traci swoje właściwości magnetyczne.

Kolejną cechą zarezerwowaną tylko dla ferromagnetyków jest histereza. Zjawisko to przejawia się w dwóch cechach ferromagnetyków: namagnesowanie ciała nie zależy tylko od natężenia pola magnesującego, ale również od namagnesowania próbki w chwili t=0. Powyższą sytuację można przedstawić na wykresie, tzw. pętli histerezy.

Włączając pole magnetyczne magnesujące próbkę. W czasie t=1, histereza osiąga swój szczytowy punkt A. Wyłączamy pole magnetyczne (punkt B). Można stwierdzić, że próbka jest namagnesowana, pomimo braku pola magnetycznego. Aby namagnesowanie próbki „zniknęło”, należy przepuścić przez zwojnicę prąd o przeciwnym zwrocie do prądu płynącego w zwoju od czasu t=0 do t=1.

DIAMAGNETYKI. Diamagnetykami są ciała, które poddane działaniu pola magnetycznego, są z niego wypychane. Można to zjawisko przedstawić w następującym doświadczeniu:

diamagnetyk	Ferromagnetyk

Diamagnetykami są substancje zbudowane z cząstek wykazujących moment magnetyczny tylko w obecności pola zewnętrznego. Diamagnetykami są: gazy, złoto, srebro, miedź, diament.

PARAMAGNETYKI. Atomy, z których zbudowane są paramagnetyki, mają nieskompensowane momenty magnetyczne. Duże energie dostarczane w formie wysokich temperatur niszczą to uporządkowanie.

RÓWNANIA FALOWE W MATERII:

Rozważmy równania (3.16), (3.17), (3.18), (3.19) oraz równania materialne (3.20) i (3.21):

/

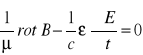
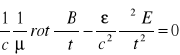
(3.25)

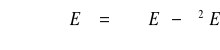
(3.26)

Z równania (3.26) wynika, że:

Równanie (3.25) przyjmuje postać (po uwzględnieniu powyższego równania):

(3.27)

Równanie fali elektromagnetycznej w ośrodku izotropowym wyrażamy wzorem:

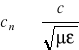
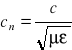
(3.28)

gdzie:
- współczynnik załamania światła w danym ośrodku ( dla próżni n=1)

Związek dyspersyjny dla fal można przedstawić następująco:

=>
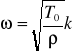
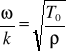
(3.29)

Fale, dla których związek dyspersyjny jest wartością stałą
, nie ulegają dyspersji. Natomiast dla fal ulegających dyspersji
zależy od długości fali. Fale sinusoidalne są falami ulegającymi dyspersji. Bardzo ważną cechą związku dyspersyjnego jest to, że zależy on od własności fal i od własności ośrodka, a nie zależy on od warunków brzegowych.

4. Teoria względności.

4.1. Narodziny nowej mechaniki (teorii względności).

Początek omawiania teorii względności na wykładzie z elektrodynamiki zawsze zaczyna się od pytań, z których jedno jest najważniejsze: co rozumiemy pod pojęciem „względność”? Odpowiedzi są różne i często błędne, czasami pada stwierdzenie, iż „wszystko jest względne”. Jedno jest pewne: po zakończeniu okresu przeznaczonego na naukę podstaw tej teorii, odpowiedzi studentów ulegały diametralnej zmianie.

W tworzeniu teorii względności, przełomem okazał się rok 1895 , kiedy H. Lorentz wyprowadził i zinterpretował wzory które łączą współrzędne w dwóch inercjalnych układach odniesienia, poruszających jeden względem drugiego z prędkością v. W 1898 to Poincarè, opublikował: „La mesure du temps”, w którym wytłumaczył sens transformacji czasu. Można wspomnieć oraz 5 czerwca, 30 czerwca i 23 lipca 1905 roku, kiedy ukazały się artykuły Poincarè oraz Einsteina, ostatecznie ustalających zarys tej teorii. Wielopokoleniowy przebieg prac nad tą teorią został przedstawiony poniżej. Szczegółowe porównanie prac Poincarè oraz Einsteina znajduje się w Dodatku D.

1864 - J.C. Maxwell - równania „Maxwella” wyrażające związki pomiędzy polami
i

oraz gęstością ładunku.

1879 - Michelson i Morley - prędkość światła (fal elektromagnetycznych) w próżni jest stała

i wynosi c.

1895 - H.A. Lorentz publikuje postać transformacji wiążącej współrzędne czasowe

z współrzędnymi czasowymi (transformacja Lorentza)

1897 - W. Kaufmann - zmiana wartości
wraz ze zmianą prędkości elektronu.

1898 - H. Poincarè - „La mesure du temps” ( Pomiary czasu ).

1898-1905 - Zaprzyjaźnieni Lorentz oraz Poincare „spierają się” o postać czasoprzestrzeni.

1900 - H. Poincarè - Obserwuje zależność dla odrzutu cząstek podczas promieniowania:

, która jest równoważna

podczas promieniowania.

1902 - H. Poincarè - „La Science et l'hypothèse” ( Nauka i hipoteza ).

1904 - H.A. Lorentz - „Electromagnetic phenomena in a system moving with any velocity

less than that of light” ( Zjawiska elektromagnetyczne w układach poruszających się

z prędkościami mniejszymi od prędkości światła ).

1904 - konferencja w St. Louis w trakcie której Poincare zaproponował, aby zasadę

względności dołączyć do pięciu klasycznych zasad fizyki:

". . . the principle of relativity, according to which the laws of physical phenomena should be the same, whether for an observer fixed, or for an observer carried along in a uniform movement of translation, so that we have not or could not have any means of discerning whether or not we are carried along in such a motion."(H. Poincarè)

5 czerwiec 1905 - H. Poincarè - Sur la dynamique de l'èlectron (Paris) (O dynamice

elektronu)

30 czerwiec 1905 - A. Einstein - Zur Elektrodynamik der bewegten Körper.

23 lipiec 1905 - H. Poincarè - Sur la dynamique de l'èlectron (Palermo) (O dynamice

elektronu)

5 maj 1920 - A. Einstein - L'èther et la teorie de la relativitè - konferencja w Leidzie.

4.2. Transformacja Lorentza.

Słuszność transformacji Lorentza jest bazą działania teorii względności. Wyraża ona związki między współrzędnymi przestrzennymi i czasowymi w rożnych układach odniesienia. Cechą transformacji Galileusza było założenie o absolutności czasu - czas „płynął” dla każdego układu jednakowo [patrz: rozdział 1. Układy inercjalne]. Teoria względności inaczej definiuje pojęcie czasu. Jego względność ujęta została w transformacji Lorentza.

Wzory na transformację Lorentza:

można uzyskać wykazując niezmienniczosc formy operatorów równania dla fali elektromagnetycznej w próżni dla układów L i L' ( □ i □'):

□ = □'

(4.3)

Startując z prawej strony równania (4.3) otrzymujemy dla dowolnej funkcji falowej U:

(4.4)

(4.5)

(4.6)

(4.7)

Podstawmy równości (4.6) i (4.7) do (4.3):

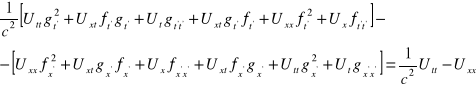
Porównując obie strony otrzymujemy:

(4.10)

(4.11)

(4.11.1)

(4.11.2)

(4.12)

Z (4.11.1) i (4.11.2) wynika, że funkcje
i
są liniowe

Wprowadźmy oznaczenie:

(4.8)

(4.9)

Uwzględniając (4.8) i (4.9) w (4.10)-(4.12) otrzymujemy:

(4.13)

=>
(4.14)

(4.15)

Przeskalowywując:


, gdzie
to prędkość jednego układu względem drugiego, otrzymamy (aby przybliżyć rozwiązanie problemu, przyjęliśmy:
oraz
):

(4.15a)

Układy cechuje pewna symetria, tak więc:
,
,
,
, oraz uwzględniając przeskalowanie:

(4.15b)

oraz

(4.15c)

Porównując (4.15b) oraz (4.15c) otrzymamy zależność:

(4.15d)

czyli ostatecznie transformacja przyjmuje postać:

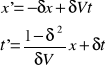
gdzie:

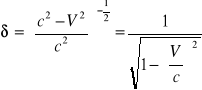
Transformacja Lorentza (dla ruchu w jednym wymiarze przestrzennym):

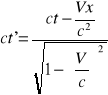
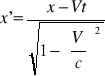
Transformacja Lorentza jest skutkiem działania teorii względności. Wiąże ona związki między współrzędnymi: przestrzennymi i czasowymi. Opisuje ona przeskalowanie współrzędnych jednego układu inercjalnego w drugi. W przypadku przestrzeni czterowymiarowej (trzy współrzędne położenia i współrzędna czasowa) mówimy o czterowektorze współrzędnych (ct,x,y,z).

4.3. Grupa Lorentza.

Zjawiska opisywane przez mechanikę klasyczną można przedstawić w przestrzeni rzeczywistej (euklidesowej), w której iloczyn skalarny definiujemy następująco:

(4.16)

W przestrzeni euklidesowej obowiązuje geometria kołowa. Oznacza to, iż iloczyn skalarny jest sumą iloczynów poszczególnych składowych dwóch wektorów (jak np. 4.16). W przestrzeni czterowymiarowej
, w która stanowi podstawę własności grupy Lorentza, iloczyn skalarny definiujemy jako:

(4.17)

co możemy zapisać również jako:

(4.18)

gdzie:

przy czym
definiujemy następująco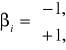

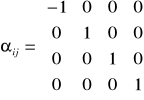
oraz:

Iloczyn skalarny wektorów czterowymiarowych, tak jak w przypadku trójwymiarowym, zachowuje się (ma tę samą wartość we wszystkich układach inercjalnych):

w 3D (4.18.a)

lub

w 4D (4.18.b)

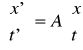
Czteroprzestrzeń, nazywanej również czasoprzestrzenią i oznaczaną jako
(3 współrzędne przestrzenne i czas), opisywana jest za pomocą geometrii hiperbolicznej. Geometria ta została wprowadzona przez znak minus w członie
, a to oznacza, iż nie można zrównywać współrzędnych przestrzennych ze współrzędną czasową. Powód: iloczyn skalarny (4.17), może przyjmować wartości:

(4.19)

wtedy mówimy, że
jest wektorem czasowym,

(4.19.a)

wtedy mówimy, że
jest wektorem przestrzennym,

(4.19.b)

wtedy mówimy, że
jest wektorem zerowym.

Zgodnie z postulatami mechaniki relatywistycznej, prędkość światła jest prędkością graniczną. Ciała materialne poruszają się z prędkością mniejszą od
, a to oznacza, ze spełnione jest równanie (4.19). Oznacza to, iż wektor
jest wektorem typu czasowego, który może przyjmować wartości dodatnie, gdy
lub ujemne, gdy
.

4.4. Stożek świetlny. Czasoprzestrzeń

Chcąc graficznie przedstawić ruch, np. fali elektromagnetycznej lub ciała materialnego, wygodnie jest posłużyć się tzw. „stożkiem świetlnym”, tj. wykreśleniem zależności położenia od czasu. Prędkość fali jest po prostu kątem nachylenia krzywej do osi ct.

Rys.4.1. Na rysunku, zgodnie z przyjętą konwencją, dokonano obrotu „stożka świetlnego” o kąt
.

W chwili t=0 badany obiekt znajduje się w początku układu współrzędnych. Stożek świetlny określa zachowanie się układu. Jak wiemy, górną granicą prędkości jest prędkość światła c. Światło na powyższym rysunku będzie rozchodzić się pod kątem 45^o do osi ct. Wszystkie inne ciała materialne poruszające się z prędkością mniejszą niż c, będą poruszać się pod kątem mniejszym niż 45^o, aż do kąta 0^o włącznie. Krzywą po której porusza się układ, czyli jego trajektorię ruchu, nazywamy linią świata. Odległości w stożku świata możemy wyrażać za pomocą odległości czasowych lub odległości przestrzennych. Są one równoważne.

Pomostem pomiędzy czasem a przestrzenią jest teoria względności. W przestrzeni trójwymiarowej pojawia się dodatkowa składowa - czas. Przestrzeń, na której określona jest składowa czasowa, nazywamy czasoprzestrzenią (czasoprzestrzenią Minkowskiego). Czasoprzestrzeń określamy za pomocą czterech współrzędnych (t,x,y,z), gdzie x,y,z są współrzędnymi kartezjańskimi, a t to wspomniana wyżej współrzędna czasowa. Rozważając przypadek stożka świetlnego, dla czasów dodatnich (t>0) mamy do czynienia z przyszłością, czas ujemny oznacza przeszłość. t=0 to chwila obecna. Powyższe stwierdzenie jest bardzo ważne, gdyż w przestrzeni Minkowskiego miarą odległości jest czas.

Referencje do rozdziału: 4. Teoria względności:

[1] Poincarè H., La mesure du temps, Revue de mètaphysique et de morale,1898.

[2] Poincarè H., La Science et l'hypothèse, Edition Flammarion, Paris, 1902.

[3] Poincarè H., Sur la dynamique de l'èlectron, Comptes rendus Acad. Sci. Paris, pages 1504-

1508, 5 Juin 1905.

[4] Poincarè H., Sur la dynamique de l'èlectron, Rendiconti del Circolo Matematico di Palermo, pages 129-175, 23 Juillet 1905.

[5] Lorentz H.A., Electromagnetic phenomena in a system moving with any velocity less than

that of light, Proc. Rogal Acad. Amsterdam, page 809, 1904.

[6] Einstein A., Zur Elektrodynamik der bewegten Körper, Annalen der Physik, pages 891 -921, 20 June 1905.

[7] Einstein A., L'èther et la teorie de la relativitè, konferencja w Leidzie, 1920.

[8] А. Пуанкаре, О науке, Издательство «Наука»,1983.

[9] S.B. Leble, S. P. Kszewiecki, Matematyczne metody teoretycznej fizyki, KGU, Kaliningrad 1995.

[10] M. Hammermesh, Teoria grup w zastosowaniu do zagadnień fizycznych, PWN, W-wa 1968.

[11] B. Thidé, Electromagnetic Field Theory, Upsilon Books Uppsala, Sweden 2004.

5. Fale elektromagnetyczne.

5.1. Odbicie fali elektromagnetycznej.

□

Rozważmy równania:

(5.1)

(5.2)

oraz

=>

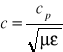
gdzie:

- prędkość światła (fali) w ośrodku

- prędkość światła (fali) w próżni

Z powyższych równań wynika zależność pomiędzy wektorami k, B i E, którą można przedstawić następująco:

(5.3)

Widzenie zawdzięczamy zjawiskom fizycznym: odbiciu i rozproszeniu światła na granicy ośrodków. Załamanie się światła jako fali elektromagnetycznej opisywane jest przez równania Maxwella.

Przedstawmy to na przykładzie:

Liczba falowa k odpowiada za kierunek propagacji fali.

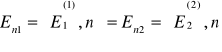
(5.4)

(5.5)

(5.6)

(5.7)

Rozważmy punkt graniczny r. Z równań (5.5) i (5.6) wynika zależność:

(przy dowolnym t)

~

Poddajmy analizie ośrodek izotropowy, gdzie:

(5.8)

(5.9)

(5.10)

(5.11)

będą warunkami brzegowymi.

Powyższy przypadek można opisać wzorami wyprowadzonymi wcześniej: (5.1) i (5.2):

(5.1)

(5.2)

5.2. Wyprowadzenie współczynników załamania.

(5.12)

gdzie:

- składowe wektora normalnego.

Załóżmy, że z=0 (analizujemy powyższe rysunki).

,
,

Pole w ośrodku 1 możemy opisać następująco:

(5.13)

,

gdzie:

- fala padająca

- fala odbita

Wykorzystując uzyskane dotychczas zależności otrzymujemy:

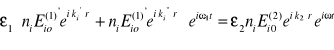
(5.14)

gdzie:

- rzut na wektor normalny

Równanie (5.14) musi być spełnione tożsamościowo (w czasie, w każdym miejscu musi być stałe). Oznacza to, że:

i

oraz współczynnik załamania

(5.15)

Przypomnijmy jeszcze raz równanie (5.14) w postaci:

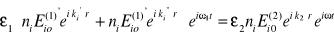
Nasuwa się pytanie: Kiedy równanie (5.14) jest prawdziwe?

Powyższa równość zachodzi tylko wtedy, gdy związki pomiędzy k i r można scharakteryzować następująco:

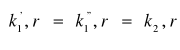
(5.16)

k i r muszą być proporcjonalne, oznacza to również, że kąty
i
( przedstawione na rysunku) są równe, tzn.:

(5.17)

PRAWO SNELIUSA

Gdy współczynnik załamania w ośrodku 2 jest większy niż w ośrodku 1, fala ulega załamaniu w kierunku do normalnej (sytuacja przedstawiona na rysunku). Gdy współczynnik załamania w ośrodku 2 jest mniejszy niż w ośrodku 1, fala ulega załamaniu w kierunku od normalnej.

Analizując równanie (5.14) oraz zależność (5.7), możemy zapisać:

(5.18)

gdzie:

- prędkości fali w ośrodku 1 i 2.

WSPÓŁCZYNNIK ZAŁAMANIA

Jak współczynnik załamania zależy od częstości
?

W myśl zasady korespondencji Bobra, teoria klasyczna i teoria kwantowa są sobie „bliskie” w przypadku, gdy energia atomu jest duża w porównaniu ze zmianą energii zachodzącą w badanym procesie, możemy wprowadzić następującą zależność:

mechanika klasyczna ~ mechanika kwantowa (zależna od czasu)

Zastosujmy teorię ruchu klasycznego do drgań elektronów w atomach. Chodzi nam o model:

Każdy elektron w atomie pod wpływem pola elektrycznego zmienia średnie współrzędne.

Schematyczny rysunek atomu przed włączeniem pola elektrycznego.	Schematyczny rysunek atomu po włączeniu pola elektrycznego.

Zgodnie z teorią Lorenza (teoria względności), atom z jednym elektronem możemy potraktować jako drgający oscylator harmoniczny a działające na niego pole elektryczne jako siłę wymuszającą.

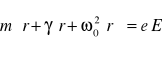
(5.19)

gdzie:

m - masa elektronu (zbliżona do spoczynkowej)

Równanie (5.19) możemy rozwiązać za pomocą transformacji Fouriera.

gdzie kierunek osi x jest taki sam jak kierunek pola E.

(5.20)

gdzie:

P- wektor polaryzacji dla fali płaskiej

Powyższy opis jest opisem kwaziklasycznym przedstawiającym model jednego elektronu.

W ośrodku izotropowym możemy zdefiniować następujące równania:

(5.21)

(5.22)

(5.23)

(5.24)

(5.25)

gdzie:

- podatność elektryczna

- częstość drgań każdego elektronu (
)

- oddziaływanie zależy od otoczenia

Rozwijając równanie (5.24) wykorzystując równość (5.20):

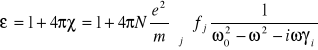
(5.26)

gdzie:

- współczynnik wprowadzony przez Lorenza oznaczający siłę oscylatora.

, gdzie Z jest ładunkiem jądra (tak jak w teorii atomów). Aby policzyć
trzeba zastosować mechanikę kwantową.

Wykres równania (5.26)

5.3. Plazma

Plazmą nazywamy zjonizowany gaz o odpowiedniej koncentracji swobodnych nośników ładunków elektrycznych w postaci jonów dodatnich i ujemnych elektronów. W skład plazmy wchodzą cząstki naładowane i obojętne elektrycznie. Sumaryczny skład ładunków plazmy jest stały, tak więc ilość ładunków przed i po jonizacji jest stała. Ruch cząstek wywołany głównie przez wysoką temperaturę może spowodować, iż wystąpią obszary o niejednorodnym rozkładzie ładunków elektrycznych. Nie mają one jednak wpływu na plazmę jako na całość. Plazmę możemy określić jako kwaziobojętną. Badając plazmę, spotkamy się ze zjawiskiem ekranowania. Ekranowanie cząstki polega na grupowaniu się wokół niej cząstek naładowanych przeciwnie. Każdą cząstkę z cząstkami ekranującymi można traktować jako elektrycznie kwazineutralną. Do opisu zjawiska ekranowania posługujemy się promieniem ekranowania (promieniem Debye'a):

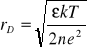
(5.27)

Promień Debye'a jest bardzo „wygodny” w opisie parametrów plazmy. Korzystając z jego własności możemy sformułować nową definicję plazmy:

Zjonizowany gaz o różnoimiennych ładunkach elektrycznych nazywamy plazmą, jeżeli promień Debye'a jest mały w stosunku do objętości zajmowanej przez gaz.

Parametry plazmy: (własności charakteryzujące plazmę)

- plazma jako pojedyncza cząstka:

- masa m

- ładunek q

- średnia objętość na jedną cząstkę

- średnia energia cząstki kT

- plazma (n cząstek):

- gęstość masy nm

- gęstość ładunku nq

- stopień jonizacji α

- gęstość energii kinetycznej nkT

Do opisu plazmy stosujemy następujące wielkości fizyczne:

- magnetyczna liczba Reynoldsa
, charakteryzująca stosunek indukcji magnetycznej pola prądów indukowanych do indukcji pola zewnętrznego

(5.29)

- liczba Alfΰena Al., która jest równa stosunkowi gęstości energii pola magnetycznego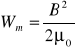
do gęstości energii kinetycznej
.

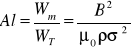
(5.30)

- liczba Stewarta

(5.31)

- liczba Hartmana

(5.32)

- parametr plazmowy

(5.33)

Dobrymi modelami „plazmy” mogą być:

- metale (swobodne elektrony)

- gazy (zjonizowane)

- promieniowanie zewnętrzne

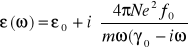
(5.34)

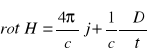
(5.35)

gdzie:

- określa ładunki swobodne

(prawo Ohma) (5.36)

(5.37)

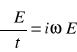
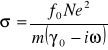
(5.38)

Rozważmy granicę dużych częstotliwości:

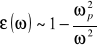
(5.39)

gdzie
- częstość plazmowa
(5.40)

oraz zależność
(5.41)

Rozpatrzmy przypadek jonosfery:

Na elektrony jonosfery można patrzeć jako na kwaziobojętną. Z równania (5.41) wynika, że k jest urojone przy
(oznacza to, że fala znika w warstwie).

Gdy
fala ma nieskończoną długość.

Otaczająca Ziemię jonosfera jest zbudowana głównie ze zjonizowanych cząsteczek
i
. Za stan jonizacji odpowiedzialne jest promieniowanie ultrafioletowe pochodzące głównie ze Słońca. Plazma jest elektrycznie obojętna, jednak mogą się tworzyć lokalne miejsca, gdzie znajduje się więcej ładunków jednoimiennych. Skutkiem tego jest słabe pole elektryczne, które działając na ładunki powoduje ich ruch. Ruch ładunków likwiduje lokalny nadmiar ładunków jednoimiennych.

Rozważmy plazmę zamkniętą w sześcianie:

Jedna ścianka jest naładowana dodatnio, druga ujemnie. Pomiędzy ściankami powstaje pole elektryczne, które możemy wyrazić wzorem:

(5.42)

gdzie:

S - powierzchnia ścianki

q - ładunek ścianki

Ruch ładunków powoduje powstawanie siły. Masa jonu dodatniego jest dużo większa od masy elektronu (minimum około 1800 razy), więc ruch elektronów bezie ruchem dominującym. Możemy więc przyjąć, że pod wpływem pola
poruszają się tylko elektrony.

Oznaczmy przez:

m - masa elektronu

e - ładunek elektronu (jednostkowy)

Siły działające w naszym układzie muszą się równoważyć:

(5.43)

Różnicę ładunków Q pomiędzy ściankami (+) i (-), powodowaną przez ruch ładunków, można opisać wzorem:

(5.44)

(5.45)

Podstawiając do równania (5.45) równanie (5.43) oraz różniczkując otrzymujemy rozwiązanie równania (5.45) w czasie:

(5.46)

oraz
- częstość oscylacji plazmy.

Jonosfera otaczająca Ziemię jest przykładem ośrodka, który ma własności dyspersyjne przy częstościach wyższych od częstości progowej. Dla częstości mniejszych od oscylacji plazmy (częstości progowej) ma własności reaktywne.

(5.47)

(5.48)

Plazma jako ośrodek reaktywny odbija fale a jako ośrodek dyspersyjny rozprasza (pochłania). Oscylacje plazmy są z zakresu 10-30 MHz.

5.4. Falowody

Falowód - walec metalowy wydrążony wewnątrz, bez przewodu wewnętrznego, którego przekrój poprzeczny może być dowolnego kształtu.

Pole magnetyczne jest obecne w falowodzie tylko w obszarze ograniczonym metalem. Posiada składowe poprzeczne i podłużne. Prędkość fazowa fali propagującej (może być większa od c) zależy od częstości (dyspersja).

Pole elektryczne o składowej podłużnej danej fali nazywamy falą elektryczną. Pole magnetyczne o składowej podłużnej danej fali nazywamy falą magnetyczną.

Fala elektryczna:
;
,

Fala magnetyczna:
;
.

Niezależnie od sposobu wzbudzenia monochromatycznego pola elektromagnetycznego w falowodzie, pole to jest zawsze sumą elektrycznych i magnetycznych fal (poza źródłami).

Pole na powierzchni i wewnątrz przewodnika.

Gdy pole się zmienia, cząstki „przeszkadzają” polu.

Rozważmy „dobry” ale nie doskonały przewodnik.

Pole w pobliżu powierzchni zachowuje się jak dla doskonałego przewodnika, ale wewnątrz przewodnika jest ono tłumione wykładniczo na pewną odległość. jest głębokością wnikania (w dobrych przewodnikach głębokość wnikania wynosi 1cm.).

Warunki brzegowe:

(5.49)

(5.50)

(5.51)

(5.52)

gdzie:

- oznacza ładunek powierzchniowy

- określa prąd powierzchniowy

Powyższe warunki brzegowe są warunkami ciągłości. Są one spełnione poza cienkim obszarem przejściowym przy powierzchni.

(5.53)

Prawo Ohma
traci ważność wskutek działania równania (5.50).

Zastosujmy metodę kolejnych przybliżeń:

1. Przy zewnętrznej stronie powierzchni występuje jedynie normalne pole elektryczne (dlatego zanika pole oraz przyspieszenie ładunków).

Przybliżenie: przewodnik idealny, składowa styczna znajduje się na powierzchni.

Na podstawie warunków brzegowych i równań Maxwella obowiązujących wewnątrz przewodnika znajdujemy pole warstwy przejściowej.

Problem: Skąd „wziąć” opis zaniku pola w przewodniku?

Rozwiązując równanie Maxwella wewnątrz przewodnika wykorzystamy właściwość, iż przestrzenne zmiany w kierunku normalnym do powierzchni są szybsze niż w stycznym. Oznacza to, że możemy „zaniechać” pochodne.

Jeżeli istnieje pole styczne do warunków brzegowych (5.53), to takie same warunki muszą istnieć pod powierzchnią.

(5.53) =>

(5.54)

Równanie (5.54) jest przybliżeniem, gdyż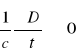
.

(5.55)

Równanie (5.55) możemy otrzymać z zależności:

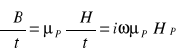
Niech
będzie wektorem skierowanym na zewnątrz. Wprowadźmy współrzędną ξ:

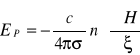
(5.56)

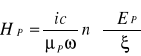
(5.57)

Wstawiając (5.56) do (5.57):

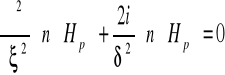
(5.58)

(5.59)

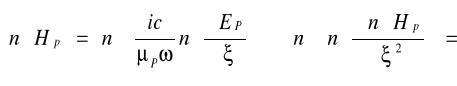
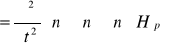
(5.60)

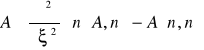
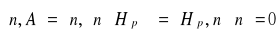
Głębokość wnikania:

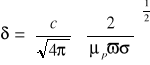
(5.61)

(5.62)

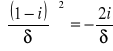
(5.63)

Uwzględniając warunki (5.62) oraz (5.63), równanie (5.56) będzie miało postać:

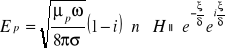
(5.64)

Własności powyższych równań:

-
,
,

- występuje różnica faz,

-
,

- pola w przewodniku są równoległe do powierzchni (równanie (5.65)).

Wzory dla pól wewnętrznych. Warunki ciągłości:

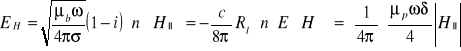
(5.65)

oznacza, że bierzemy pod uwagę pole wzdłuż falowodu.

FALOWODY CYLINDRYCZNE

Rozważmy przypadek metalowych cylindrów (pustych).

W przypadku gdy
mamy do czynienia z falowodem. Gdy długość l jest porównywalna z promieniem R, mówimy wtedy o rezonatorze.

Przyjmujemy pewne udoskonalenie powyższego falowodu. Otóż zakładamy, że jego ściany są doskonałymi przewodnikami. Straty energii są powodowane głównie skutkiem ogrzewania się falowodu. Kształt przekroju nie ulega zmianie.

Jednorodność falowodu na osi z pozwala pozbyć się pochodnych po z (pochodna ma wartość stałą).

W ośrodku stałym, izotropowym:

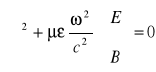
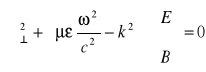
(5.66)

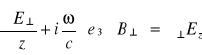
(5.67)

(5.68)

(5.69)

(5.70)

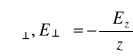
(5.71)

(5.72)

Rozważmy falę poprzeczną (TEM):

(5.73)

(5.74)

(5.75)

(5.76)

Równania (5.75) i (5.76) są rozwiązaniem dwuwyrazowego rozwiązania elektrostatycznego.

Wniosek:

1) Fale TEM nie mogą istnieć wewnątrz pojedynczego pustego cylindrycznego przewodnika o nieskończonym przewodnictwie. Powierzchnia przewodnika jest powierzchnią ekspotencjalną - pole wszędzie znika. Musimy zastosować kabel koncentryczny lub linię dwutransmisyjną.

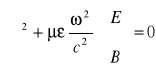
(5.77)

dla fal TEM

2)

3) dla fal płaskich

W pustych walcach:

dla

Warunki brzegowe:

(5.78)

1)
- wszędzie fale magnetyczne poprzeczne TM.

TM:
(5.79)

2) Fale podłużne TE.

(5.80)

dla obu fal zachodzi związek:

(5.81)

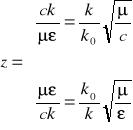
(5.82)

(5.83)

(5.84)

(5.85)

=>
(5.86)

Po przekształceniu równania (5.85) otrzymujemy:

(5.87)

FALOWODY DIELEKTRYCZNE (ŚWIATŁOWODY):

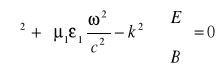
(5.88)

Warunki brzegowe:

W zmiennych walcowych:

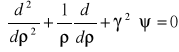
(5.89)

Równanie (5.89) jest rozwiązaniem funkcji walcowej.

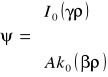
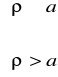
gdzie: A - pewna stała.

Wybór funkcji zależy od warunków brzegowych.

Dla fal TE:

(5.90) (5.91) (5.92)

(5.93) (5.94) (5.95)

Występuje symetria, więc pochodna po φ się zeruje. Oznacza to, że równania (5.90) i (5.93) są równe:

(5.96)

(5.97)

Równanie (5.96) można rozwiązać numerycznie lub graficznie:

5.5. Tłumienie falowodów

Tłumienie falowodów występuje na wskutek strat na ścianach falowodu o skończonym przewodnictwie.

(5.98)

(5.99)

(5.100)

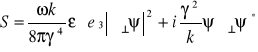
(5.101)

gdzie:

- wektor Poyntinga.

Wektor
jest wektorem przestrzennym.

A - przekrój poprzeczny

(5.102)

gdzie:

- potencjał,

- gradient poprzeczny.

Korzystamy z tożsamości Greena:

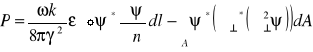
(5.103)

gdy: lub

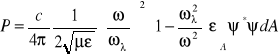
(5.104)

Energia pola niejednorodnego:

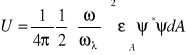
(5.105)

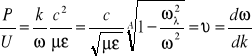
(5.106)

Jeżeli występuje przewodnictwo skończone (sytuacja rzeczywista) straty wynikają z prawa Ohma.

(5.107)

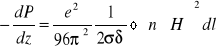
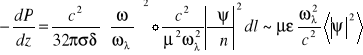
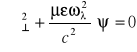
Z prawa Ohma
,
- głębokość wnikania.

Dla fal TEM, TE, TM:

istnieje pewna geometria (symetria),

warunki brzegowe są warunkami ciągłości.

5.6. Dyfrakcja fal

Rozważając dyfrakcję fal rozpatrujemy skończoną długość fal.

Tożsamość Greena:

Twierdzenie Greena:

(5.108)

Metoda Kirchoffa (skalarna)

każde równanie w próżni.

(5.109)

Równanie (5.109) jest równaniem Helmholza.

(5.110)

,
(5.111)

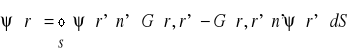
(5.112)

Wzór Kirchoffa:

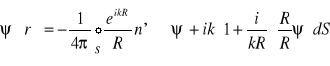
Zagadnienie dyfrakcji może być sformułowane w taki sposób:

Wzór Kirchoffa przyjmuje postać:

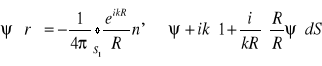
(5.113)

,

Przybliżenie:

1) poza otworami w

Wzór (6) daje:

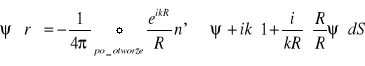
Rozpraszanie na małej kuli dielektrycznej:

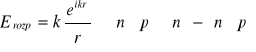
gdzie:

oraz

52

38

---