1. DEFINICJA DZIEDZINY FOTOGRAMETRIA I TELEDETEKCJA.
Zaktualizowany na XVI-ym Kongresie w Kioto w 1988 r. statut Międzynarodowego Towarzystwa Fotogrametrii i Teledetekcji podaje łączną definicję fotogrametrii i teledetekcji następująco: jest to dziedzina nauk technicznych zajmująca się pozyskiwaniem wiarygodnych informacji o obiektach fizycznych i ich otoczeniu drogą rejestracji pomiaru i interpretacji obrazów lub ich reprezentacji numerycznych otrzymywanych z sensorów nie będących w bezpośrednim kontakcie z tymi obiektami.Cechy:
*brak kontaktu z badanym obiektem
*szybki czas pozyskiwania informacji masowej
*niezalezna wielokrotna mozliwość opracowania danych(inf.punktowe i liniowe,wektorowe).
Technologie fotogrametryczne:
a)areorniangulacja: zagęszczenie osnów geodez.
b)ortofotomapa cyfrowa(mapa fotograficzna)
c)numeryczny model terenu DTM(NMT)
d)mapa numer.+aktualizacja.
2. PODZIAŁ FOTOGRAMETRII NA DZIAŁY I METODY OPRACOWANIA ZDJĘĆ.
Fotogrametria jest więc złożoną dziedziną posiadającą wiele różnych gałęzi, między innymi(metody opracow. fotogrametrycznego):
- fotogrametrię analogową - gałąź fotogrametrii, która zaczyna się, na zięciach, a kontynuowana jest na optycznych instrumentach,
- fotogrametrię analityczną - gałąź fotogrametrii, która zaczyna się, podobnie na zdjęciach i kontynuowana jest na skomputeryzowanych instrumentach,
- fotogrametrię cyfrową - gałąź, w której obraz nie jest rejestrowany fotogrametrycznie lecz przy pomocy elektroniki w postaci cyfrowej, gdzie następnie techniki komputerowe stymulują wizją i rozpoznawaniem.
Działy:
*lotnicza(aerofotogrametria)
*naziemna
*satelitarna(zobrazowania satelitarne)
+soft copy photogrametry(na nośnikach z oprogam.)
+hard copy photogrametry(z wyplotu)
# fotogram. bliskiego zasiegu :ze wzgled.na specyfike wykonywanych zdjęć
3.PROMIENIOWANIE ELEKTROMAGNETYCZNE WYKORZYSTYWANE DO REJESTRACJI OBRAZÓW FOTOGRAMETRYCZNYCH.
Promieniowanie elektromag.- emitowane przez rozbudzone cząsteczki i atomy:
*ultrafiolet
*widzialne(0,4-0,7 um)na nie skladają się :
-B(niebieska)0,4-0,5
-G(zielona)0,5-0,6
-R(czerwona)0,6-0,7
*bliska podczerwień(0,7-1,3)
*daleka podczerwień(7-15)
promieniowanie nadfioletowe wchodzi w skład widma elektromagnetycznego i zajmuje obszar falowy w granicach 10-400 nm. Chociaż nadfiolet przylega do widma widzialnego i na ten właśnie zakres promieniowania przypada maksimum uczulenia halogenków srebra, stanowiących podstawowy składnik światłoczułych materiałów fotograficznych, to jednak jest to jeden z najmniej zbadanych zakresów promieniowania elektromagnetycznego.
widmo widzialne, czyli światło. Metod, rejestrującą informacje otrzymywane w tym zakresie widma jest fotografia.Jak wiadomo, istnieje grupa związków chemicznych, w których pod wpływem działania światła następują zmiany w ich budowie Substancje te są określane jako światłoczułe a reakcje chemiczne wywołane pod wpływem światła nazywa się reakcjami fotochemicznymi
promieniowanie podczerwone obejmuje znaczną część widma elektromagnetycznego.Cały ten ogromny obszar podczerwieni podzielono umownie na trzy podzakresy. Pierwszy z nich obejmuje promieniowanie o długości fali 760-1500 μm, zwane podczerwienią bliską lub niekiedy podczerwienią fotograficzną, gdyż można ją rejestrować na odpowiednio uczulonym filmie fotograficznym. Drugi podzakres stanowi podczerwień środkowa, w granicach 1,5-10,0 μm. Wreszcie trzeci, od 10,0 do 1000 μm, to długofalowe promieniowanie podczerwone, zwane także podczerwienią daleką.
Mikrofale obejmują one zakres między długofalowym promieniowaniem podczerwonym a krótkimi falami radiowymi. Współczesna technika wykorzystuje jednakże tylko pewne przedziały tego zakresu promieniowania. W systemie pasywnym jest stosowane tylko promieniowanie o długości fali od 3 mm do 30 cm, natomiast w systemie aktywnym od 8,3 mm do 133 cm.
5. CECHY I WŁAŚCIWOŚCI OBIEKTYWU.
Najważniejszą częścią kamery lotniczej jest obiektyw. Składa się on z układu odpowiednio dobranych soczewek, które zapewniają powstawanie w płaszczyźnie tłowej (na matówce lub materiale światłoczułym), ostrego i odwzorowanego zgodnie z zasadami rzutu środkowego, obrazu powierzchni terenu. Obiektywy fotogrametryczne powinny być zatem wolne od dystorsji oraz odznaczać się wysoką zdolnością rozdzielczą. Cechy obiektywu:
- dł. ogniskowej(1/m=f/D-f),
- kąt widzenia(2β);tgβ=a/2f
- otwór wejściowy czynny(d) i względny (k),
- jasność obiektywu(J=En/E0 )
-zdolność rozdzielcza.
Ogniskowa obiektywu f' jest to odległość głównego ogniska obrazowego F' od głównego punktu obrazowego obiektywy.
Otwór względny obiektywu jest to stosunek średnicy otworu wejściowego obiektywu - d, do ogniskowej obiektywu - f'. (k=1/φ , k=d/f )
Kąt rozwarcia i kąt widzenia obiektywu wiąże się z polem obrazu i polem widzenia obiektywu. Polem widzenia obiektywu (rys) przyjęto nazywać podstawę stożkowej wiązki promieni, które tworzą obraz nieskończenie dalekiego przedmiotu.
Zdolność rozdzielcza obiektywu jest jedną z podstawowych wielkości cechujących jego układ optyczny. Polega ona na właściwości rozdzielnego przekazania obrazu dwóch jednakowo jasnych, blisko położonych punktów lub linii, a wartość jej jest wyrażana liczbą oddzielnie odwzorowanych linii, przypadających na l mm obrazu optycznego.
Aberracje obiektywów. Nawet najlepsze obiektywy są obarczone pewnymi wadami. Jedną z takich wad układów optycznych, polegającą na zniekształceniu przebiegu promieni świetlnych przez poszczególne elementy układu, jest dystorsja. Błąd dystorsji powstaje na skutek różnicy kątów padania promieni wchodzących do obiektywu i wychodzących z niego.
Aberracja sferyczna polega ona na tym, że wiązki światła symetryczne względem osi optycznej (równoległe do osi lub wychodzące z jednego punktu na osi) po przejściu przez obiektyw przecinają się nie w jednym punkcie (rys), lecz na pewnej powierzchni, nazywanej powierzchnią diakaustyczną. Zniekształcenie to jest spowodowane faktem, iż poszczególne strefy soczewek układu optycznego mają różne ogniska (strefy bliższe brzegu soczewki załamują promienie silniej, ponieważ mają krótszą ogniskową). W rezultacie promienie równoległe do osi obiektywu przecinają się w różnych płaszczyznach obrazowych, tworząc na matówce obraz o zróżnicowanej ostrości. Wpływ aberracji sferycznej redukuje się przez dobór odpowiednich soczewek i konstrukcję najkorzystniejszych ich układów.
Aberracja chromatyczna obiektywu (rys) jest spowodowana zróżnicowaniem współczynnika załamania promieni odpowiadających składowym barwom światła białego (najsilniej są załamywane promienie fioletowe, najsłabiej - czerwone). Rezultatem tego zjawiska jest przecięcie się promieni poszczególnych barw w różnych płaszczyznach obrazowych, co powoduje powstawanie na obrazie barwnych obwódek, a przez to zmniejszenie ostrości obrazu. Niekorzystny wpływ tej aberracji eliminuje się przez zastosowanie achromatycznych układów optycznych.
6. FORMATOWANIE I ZAPIS OBRAZU FOTOGRAFICZNEGO - PROCES NEGATYWOWY I POZYTYWOWY.
Przejście od obrazu utajonego do obrazu widocznego nazywa się wywoływaniem(redukcja z halogenkiem srebra).
Wywolywanie jest to poddanie naświetlonej emulsji działaniu pewnych odczynników chemicznych, w czasie którego naświetlone ziarenka halogenków srebra zmieniają się w srebro metaliczne. W miejscach, gdzie światło działało dłużej lub intensywniej, naświetlonych zostało więcej ziarenek halogenków srebra, mniej zaś w cieniach obrazu optycznego.Tak więc duże skupiska ziaren srebra tworzą obraz miejsc silnie naświetlonych, w postaci czarnych powierzchni (obserwacja w świetle przepuszczonym). Małe skupiska ziaren srebra tworzą obraz miejsc mniej naświetlonych, w postaci plam szarych o różnej tonacji. Tam gdzie nie powstał obraz utajony, nie ma też ziaren srebra pochłaniających światło i miejsca te są zupełnie jasne. Oglądany w takiej postaci obraz optyczny nazywa się negatywem, a to z powodu odwrócenia na nim walorów świetlnych rzeczywistego obrazu optycznego.
Przejście od obrazu negatywnego, do obrazu zgodnego z walorami świetlnymi oryginału, nazywa się procesem pozytywowym, a rezultat tego procesu pozytywem. Przejście od negatywu do pozytywu następuje na drodze kopiowania stykowego lub optycznego. Zarówno kopiowanie stykowe, jak i optyczne pozwala na uzyskanie z jednego negatywu dowolnej liczby pozytywów. Przy kopiowaniu stykowym skale negatywu i pozytywu są sobie równe. Przy kopiowaniu optycznym możliwe jest powiększenie lub pomniejszenie skali negatywu. Zazwyczaj jednak skala pozytywu jest większa od skali negatywu.
Proces negatywowy i pozytywowy składa się z tych samych grup czynności, a mianowicie : naświetlenia, wywołania, kąpieli przerywającej, utrwalenia, płukania i wysuszenia.
Proces negatywowy- polega na wytraceniu nienaświetlonych cząstek AgBr; do tego celu stosuje się wywoływacze(metol,soda);po wywołaniu negatyw się płucze i utrwala(biosiarczan sodowy)
Proces utrwalenia-nienaświet.AgBr są wypłukiwane(nie w H2o,bo w niej nie są rozp.)
Proces płukania-zmycie AgBr z warstwy nośnej mater. światłoczułego
Każdy wywoływacz składa się z czterech podstawowych substancji: redukującej, wywołującej, konserwującej, przyspieszającej i klarującej. Substancje te dobrane w odpowiednich proporcjach, są rozpuszczone w wodzie o temperaturze około 20'C.
*******************************************
Cechy sensynometryczne-związane z badaniem czułości mater.światłoczułych.
KRZYWA sensynometr.-charakteryzuje mater. światłoczuły:zwiazek między naświetleniem a zaczernieniem mat. fotograf.(D=f(lgH) H=E*t )
Czułość ogólna:SDIN ,SASA
Czułość(światloczułość)-zdolność warstwy światłoczułej po naświetl. I wywołaniu do wygenerowania określonej gęstości optycznej.Na czułość oolną istotny wpływ ma zastos.wywoływacz
Kontrastowość-charakteryzuje zdolność materiału fotograf. do rejestracji różnicowania luminacji obiektów
Czułość spektralna(barwnoczułość-Sλ)określa stopień reakcji na falę promieniowania elektromag. O określonej dł.λ
Ze względu na barwnoczułość materiały dzielimy na:
*nieuczulone „ślepe”-czule tylko na barwe niebieską
*pamchromatyczne-uczulone na zakres widzialny
*podczerwone-czułe na podczerwień
*barwne(rejestrują w zakresie RGB 0,4-0,7um)
*spekrostrefowe”false colour”
Współczynnik kontrastowości γ zależy od:
-rodzju mater. fotograf. i jego wieku
-rodzaju wywoływacza
-temp. wywoływ.
-czasu wywoł.
Zdolnośc rozdzielcza(R) -max liczba oddzielnie odfotograf. linii lub par linii na 1mm wywoływanego obrazu.Zależy od ziarnistości emulsji ,oświetlenia,kontrastu,rozproszenia światła .R=2000/P (l/mm)
Barwy substraktywne-żółty,magenta,cyjan
G+R=Y=W-B B+R=M B+G=C
10. KAMERY LOTNICZE DZIELIMY:
-kamery do wykonywania zdj. pojedynczych (migawkowe obejmujące zasięgiem ramki tłowe, wycinek fotografowanego obszaru)
-kamery szczelinowe (bez migawki), dostarczające ciągłego pasa terenu na przesuwającym się odpowiednio do prędkości lotu fil....
-kamery panoramiczne
Wg orientacji kamery dzielimy:
-kamery do wykonywania zdjęć pionowych lub prawie pionowych (w szeregach)
- kamery do wykonania zdj. perspektywistycznych (o widocznej linii horyzontu)
- kamery sprzężone - dwie kamery o wspólnym podwieszeniu o ustalonym kącie zbieżności
Zasięg pola widzenia
a) wąskokątna WK 100 - 200 600 mm
b) normalnokątna NK 500 - 750 300 mm
c) seminormalnokątna 210
d)szerokokątna SzK 850 - 950 150 mm
d) nadszerok. NSk 1100 - 1300 90 mm
Współczesne kamery lotnicze.
Przykład -RMK TOP ZEISSA - praktycznie wolna od dystorsji, jedno osobowa obsługa, spręrzone z GPS , automatyczna obsługa(urządzenie sterownicze i nawigacyjne, klawiatura).
RMK TOP 15 Ck = 30 cm
inne:
LMK 2000, LMK 300, ZEISS JENA
Elementy podstawowe:
Korpus kamery służy do pomieszczenia stożka obiektywowego, nazywanego również blokiem optycznym.
Kaseta (ładownik) - jest przeznaczona do pomieszczenia materiału światłoczułego i stopniowego przewijania go w czasie między kolejnymi ekspozycjami.
Podwieszenie służy do umocowania korpusu kamery do podłogi samolotu w ten sposób, aby obiektyw znalazł się nad otworem, przez który są wykonywane zdjęcia.
Stożek obiektywowy stanowi najważniejszy element kamery lotniczej. W dolnej części stożka jest umieszczony obiektyw, wewnątrz którego wmontowana jest przysłona i migawka aparatu
Urządzenie sterujące jest pomocniczym elementem kamery lotniczej, który reguluje rytm pracy i współdziałanie poszczególnych jej mechanizmów.
Etapami cyklu pracy kamery lotniczej są:
• przewinięcie błony fotograficznej,
• naciągnięcie migawki,
• wyrównanie błony fotograficznej w płaszczyźnie ramki tłowej,
• ekspozycja.
INTERWAŁ-czas między ekspozycjami
11. RODZAJE ZDJĘĆ LOTNICZYCH
a)Wg. Skali zdjęć:
- Małoskalowe 25 000 < Mz < 100 000
- Średnioskalowe 5 000 < Mz < 25 000
- Wielkoskalowe 500 < Mz < 5 000
b) ze względu na kąty nachylenia zdjęcia
- zdj. Pionowe v ≤ 3o - układ odniesienia - oś celowa kamery
- zdj. Nachylone v > 3o bez widocznego na zdjęciu horyzontu
- zdj. Ukośne z widocznego na zdjęciu horyzontem
12. ZDJĘCIA WYKONYWANE DLA OBSZARU POLSKI W RAMACH PROGRAMU PHARE.
W 1995 - 97(98) wykonywano w ramach programu PHARE zdjęcia lotnicze całej polski w skali 1:26 000, 1:5 000
1. 1:26 000 skala średnia - cała Polska pokryta tymi zdjęciami powstało konsorcjum firmy Eurosence + Polkart + Geokart. Zdięcia z 5 samolotów fotograficznych marki Cesna kamerami LMK 2000, LMK 3000, RC 20, RC 30 połączona z techniką GPS. Obróbka fotogrametryczna została opracowana w CODGiK. Zdjęcia z pokryciem p = 50% q = 33%. Kierunek nalotu Pu - Pd. Zdjęcia celowane ( naloty synchroniczne jako arkusz mapy 1:1000 w układzie 42 ). Kamery szerokokątne. Razem 30 000 zdjęć - aktualizacja mapy topograficzne.
2. 1:500 - dla obszaru 17 miast Polski (Olsztyn). Kamery z ogniskową normalnokątną (300 mm) i półnormalnokątną (200 mm) p = 60% q = 23 - 27%. Zdjęcia celowane, synchronizowane z krojem sekcyjnym mapy 1:1000 w układzie 92. Od 97r. wykonywano zdjęcia wraz z różnicowym pozycjonowaniem środka rzutu.
13. STEREOGRAM, SZEREG ZDJĘĆ, BLOK ZDJĘĆ?
Fotogram-pojedyncze zdjęcie
Stereogram - para odpowiednio pokrywających się zdjęć(typowa wartość:podlużne p=60-80%,poprzeczne g=20-40%), muszą one być wykonane z dwóch stanowisk -baz usytuowanych w podobnej odległości od obiektu, zdjęcia powinny być poprawnie zorientowane i nadające się do obserwacji sereoskopowej.
Szereg zdjęć - lotnicze zdjęcia pomiarowe wykonane szeregowo, pokrycie wzajemne dwóch zdjęć w szeregu stosuję się: 60% pokrycie podłużne (wzdłuż linii lotu) i 20-40% pokrycie poprzeczne (pomiędzy szeregami)
Blok zdjęć - minimum dwa szeregi.
14. PROJEKT NALOTU FOTOGRAMETRYCZNEGO
1) Skala zdjęć Mz = c √ Mp Mz=w/ck c- współczynnik Grubera
2) wysokość fotografowania w = ck Mz
3) wysokość absolutna fotografowania w = w + Zśr
4) Długość boku zdjęcia w terenie lz = lx (ly) Lz = lz Mz
5) Długość bazy (podłużnej) fotografowania przy p% Bx = Lz(1 - p% / 100)
6) Odległość między osiami szeregów przy q% As = Lz (1 - q% / 100) By=As (By - poprzeczna baza)
7) Baza fotografowania w skali zdjęcia bx = Bx / Mz
8) Odległość między osiami szeregów w skali zdjęcia as = As / Mz
9) Stosunek bazowy v = Bx / w
10) Powierzchnia użyteczna zdjęcia Pz = Lz2 = lz2 Mz2
11) Powierzchnia stereogramu Ps = (Lz - Bx) Lz
12) Powierzchnia stereogramu nowo utworzona PN = Bx As
13) Liczba szeregów w bloku ns = Q / As + 1 Q - szerokość bloku
14) ilość modeli w kolejnym szeregu nmi = S(i) / Bx + 1 Si - długość szeregu
15) Ilość zdjęć w kolejnym szeregu nz(i) = nm(i) + 1
16) ilość zdjęć w bloku nZB = ∑nZ(i)
17) Czas ekspozycji tmax \< kr Mz / V V-prędkość samolotu kr\<0.02 mm
18) Interwał fotografowania Δt = Bx [m] / V [m/s] >/ 2 s
19) Długość filmu LF = 1.1 ∑nZ(i) 22 cm (18x18) lub 28 cm (23x23)
20) Długość lotu L = 1.2 Po / As Po-powierzchnia obiektu
21) Czas lotu T = L / V
15. PARAMETRY FOTOGRAMETRYCZNEJ OCENY SZEREGU I BLOKU ZDJĘĆ LOTNICZYCH.
Po wykonaniu zdjęć lotniczych są one poddane kontroli. Kontrola jakości zdjęć dzieli się na ocenę jakości fotograficznej i fotogrametrycznej.
Ocena jakości fotograficznej powinna przebiegać na podstawie sensytometrycznych określeń wskaźników jakościowych trzech wybranych zdjęć (negatywów) z każdej błony filmowej. Są to zwykle zdjęcia początkowe, środkowe i końcowe. Pozostałe negatywy oceniane są wizualnie w porównaniu z trzema badanymi lub z negatywami wzorcowymi. Skala ocen : bardzo dobry, dobry, dostateczny i niedostateczny. Negatywy z ostatnią oceną nie powinny być dopuszczone do dalszego opracowania.
Ocena jakości fotogrametrycznej polega na sprawdzeniu : nieistnienia przerw fotogrametrycznych, prostolinijności osi szeregów, wartości kątów nachylenia zdjęć, odchylenia od zaprojektowanej wysokości fotografowania, wartości kątów skręcenia zdjęć, pokrycia podłużnego i poprzecznego.
Skręcenie zdjęć w stosunku do osi szeregu
Pokrycie zdjęć nie powinno się różnić od zadanego więcej niż ± 5%. Gdy Px<53% lub Py < 15%, to zdjęcia nie przechodzą do dalszego opracowania.
Kąty skręcenia zdjęć χ. w stosunku do osi szeregu nie powinny przekraczać ± 10°, przy dążeniu średniej wartości do 0. Systematyczne skręcanie zdjęć może spowodować choinkę (rys. 42), co jest zjawiskiem niepożądanym.
Odchylenie wysokości fotografowania W 'od zadanej nie powinno przekraczać 5%
Zdjęcia lotnicze (negatywy) o v > 3o są odrzucane, a liczba zdjęć o v > 2o nie powinna przekraczać 10%, ogólnej liczby wykonanych zdjęć.
Prostolinijność osi szeregu określana odchyleniem środka dowolnego zdjęcia od linii łączącej środki skrajnych zdjęć w szeregu nie powinna przekraczać 3% długości szeregu.
Zdjęcia z przerwami fotogrametrycznymi nie nadają się do dalszego opracowania. Zachodzi wtedy konieczność opracowania tradycyjnego - geodezyjnego lub powtórne wykonanie zdjęć.
17 UKŁADY WSPÓŁRZĘDNYCH STOSOWANE W FOTOGRAMETRII
układ współrzędnych tłowych płaski (x',y')
układ współrzędnych zdjęcia lotniczego
Rys. 2.1. Układy współrzędnych zdjęcia lotniczego: a) odniesiony do punktu głównego O', b) odniesiony do środka rzutów
- układ współrzędnych tłowych przestrzenny zdjęcia naziemnego (x',y', +- Ck=z')
- układ współrzędnych transformowanych (ukł. wsp tłowych zdjęcia po obrocie o kąty fi, kappa, omega, po którym osie są równoległe do osi lokalnego układu współrzędnych)
Układy współrzędnych terenowych O, X, Y, Z, transformowanych O'i, X'i , Y'i, Z'i i tłowych O', x', y'; ai— wektor wodzący z j ego składowymi
układy współrzędnych terenowych:
- układ współrzędnych geodezyjnych
- układ geocentryczny
lokalny układ współrzędnych XYZ
układ współrzędnych modelu
Rys. 2.8. Współrzędne modelu X', Y', Z' — układ odniesiony do osi kamery na lewym stanowisku lub X1 Y1 Z1 -odniesiony do bazy O1O2
- układ współrzędnych pikselowych
- układ współrzędnych fotogrametrycznych (zdjęcia naziemne)
19. UKŁAD WSPÓŁRZĘDNYCH TŁOWYCH
O'-punkt główny(rzut otogonalny środka rzutów na płaszczyznę tłową obrazu)
21. ELEMENTY ORIENTACJI WEWNĘTRZNEJ ZIĘCIA.
Elementami orientacji wewnętrznej zdjęcia lotniczego (rys) nazywamy wielkości umożliwiające określenie położenia środka rzutów O w stosunku do płaszczyzny zdjęcia. Elementami orientacji wewnętrznej są zatem:
* współrzędne tłowe głównego punktu zdjęcia O' (x'o, y'o lub też Δx0Δy0-poprawki do jego położenia)
*stała kamery ck (f) tj. odległość między głównym punktem obrazowym obiektywu kamery a płaszczyzną obrazu (płaszczyzną ramki tłowej). Jest ona odpowiednikiem odległości środka rzutu O od rzutni π.
*poprawka dystorsji radialnej (k0-kn ;wart. do 4um)
*popr. tangencjalnej (p0-pn ;do 2um)
22. WPŁYW CZYNNIKÓW GEOMETRYCZNO-OPTYCZNYCH NA JAKOŚĆ OBRAZU FOTOGRAFICZNEGO I CYFROWEGO (DYSTORSJA, BŁĘDY SZCZĄTKOWE OBIEKTYWU, DEFORMACJA PODŁOŻA, DEFORMACJA SENSORA CYFROWEGO, REFRAKCJA FOTOGRAMETRYCZNA, KRZYWIZNA ZIEMI)
A) Dystorsja - Jej eliminacja oparta jest na wykorzystaniu wielomianów. Krzywą dystorsji radialnej opisuje wielomian:
Δr= a0r + a1r3 + a2r5 + a3r7 + ... gdzie a - wsp. Określający kształt krzywej
Promienie radialne dla zdjęcia prawego i lewego 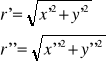
B) Szczątkowe wady obiektywów (aberacje, astygmatyzm) są we współczesnych obiektywach praktycznie zaniedbywalne
Korekcja współrzędnych tłowych zdjęcia Δrx' = x' (k0 + k1r'2 + k2r'4 + k3 r'6 + ...)
Δry' = y' (k0 + k1r'2 + k2r'4 + k3 r'6 + ...)
Gdzie![]()
C) Deformacja podłoża - np. błona negatywu może nie przylegać do płytek, lub uległa deformacji w procesie niewłaściwego przechowywania lub obróbki ( podobnie obróbka diapozytywów) mogą powodować miejscowe zniekształcenie obrazy
Eliminacja w procesie transformacji afinicznej (z wyrównaniem deformacji przypadkowych)
D) Deformacja sensora cyfrowego może powodować szumy obrazów cyfrowych. Eliminacja - filtr dolnoprzepustowy, medianowy
E) Refrakcja fotogrametryczna powoduje zwiększenie się promienia ra przy wykonywaniu zdjęć z (rys) dużych wysokości. Promienie świetlne przechodzą przez warstwy powierzchni o różnej gęstości, są odchylone (punkty przesuwają się na zewnątrz od pkt. głównego) jest to zniekształcenie radialne (w punkcie nadirowym = 0) jego wielkość wzrasta wraz ze wzrostem W i kąta α. Zarówno wpływ refrakcji jak i krzywizny ziemi uwzględnia się przy precyzyjnych opracowaniach zdjęć lotniczych.
F) Krzywizna ziemi powoduje zmniejszenie promienia ra jest to zniekształcenie zmniejszające (rys)
wymiary obrazy, przesuwające obraz punktów terenowych w kierunku punktu nadirowego.
Poprawki można wprowadzać do poszczególnych zdjęć lub modeli.
Zniekształcenie Δr proporcjonalne do wysokości lotu W, wielkość promienia radialnego r odwrotnie proporcjonalna do Ck
23. WPŁYW REFRAKCJI FOTOGRAMETRYCZNEJ I KRZYWIZNY ZIEMI.
Do grupy czynników fizycznych wpływających na zniekształcanie obrazu zdjęć lotniczych zaliczymy:
- zdolność rozdzielczą fotograficzną,
- dystorsje ,
- nieprzyleganie negatywu do płaszczyzny ramki tłowej oraz niepłaskość ramki tłowej,
- deformacje materiału światłoczułego,
- krzywiznę Ziemi,
- refrakcję fotogrametryczną.
Wpływ krzywizny Ziemi i refrakcji rozpatrywany jest łącznie. Krzywizna Ziemi powoduje zmniejszenie się promienia ra, refrakcja powoduje zwiększenie się promienia ra (rys. 77 i rys. 78). Przybliżony wzór na przesunięcie obrazu punktu terenowegoAna
Rys. 77. Wpływ krzywizny Ziemi na Rys. 78. Wpływ refrakcji na zniekształcenie zniekształcenie obrazu
zdjęciu lotniczym, z uwzględnieniem łącznego wpływu krzywizny Ziemi i refrakcji ma postać:
![]()
gdzie: R-promień kuli ziemskiej, W—wysokość fotografowania,f-stała kamery. ra -promień poprowadzony od punktu nadirowego do danego punktu zdjęcia.
Wpływ krzywizny Ziemi i refrakcji uwzględniany jest przy precyzyjnych opracowaniach zdjęć lotniczych
24. METRYKA KALIBRACJI KAMERY
Kalibracja kamer ma na celu dostarczenie charakterystyki metrycznej kamer fotogrametrycznych. Taka charakterystyka jest niezbędna do przeprowadzenia prac fotogrametrycznych i obejmuje następujące parametry:
1) odległość obrazowa kamery (stalą kamery — oznacza się przez ck lubf),
2) położenie punktu głównego kamery w stosunku do znaczków tłowych (xo , yo),
3) radialna i tangencjalna dystorsja obiektywu,
4) zdolność rozdzielcza obiektywu,
5) odległość pomiędzy znaczkami Iłowymi,
6) odchylenia ramki tłowej do płaszczyzny.
Ponadto, jeśli kamera zawiera siatkę reseau, muszą być również określone położenia znaczków „reseau" w stosunku do znaczków tłowych. Powyższe dane pozwalają na przeprowadzenie precyzyjnej geometrycznej rekonstrukcji wiązki promieni, która została zarejestrowana w kamerze podczas ekspozycji. Rekonstrukcji tej można dokonać graficznie, instrumentalnie i matematycznie.
Metody kalibracji można podzielić na polowe i laboratoryjne. Metody polowe wymagają budowy pola testowego lub wykorzystania wybranych gwiazd jako punktów o znanych współrzędnych. Do metod tych zalicza się metody statyczne i dynamiczne. Te ostatnie umożliwiają pozyskiwanie informacji do kalibracji kamer lotniczych w czasie lotu. Najczęściej stosuje się jednak metody laboratoryjne, oparte na wykorzystaniu kalibratorów wielokolimatorowych lub goniometrów, czyli kalibrację przeprowadza się metodą fotograficzną lub wizualną.
27. ELEMENTY ORIENTACJI ZEWNĘTRZNEJ ZDJĘCIA.
Elementy orientacji zewnętrznej zdjęcia lotniczego (rys) są to wielkości określające położenie kamery względem fotografowanego terenu. Umożliwiają one wyznaczenie orientacji przestrzennej wiązki promieni rzutujących w momencie wykonywania zdjęcia. Elementami tymi są:
* współrzędne przestrzenne środka rzutów Xo Yo Zo (w układzie współrzędnych prostokątnych, przyjętym do prac pomiarowych w terenie);
*ω-pochylenie poprzeczne(w poprzek osi nalotu fotograf.)
*φ-pochylenie podłużne
*κ-skręcenie zdjęcia
28. PUNKTY I LINIE SZCZEGÓLNE ZDJĘCIA.
• płaszczyznę terenu T;
• płaszczyznę zdjęcia π, nachyloną w stosunku do płaszczyzny terenu T pod kątem v;
• płaszczyznę horyzontu T, czyli płaszczyznę poziomą przechodzącą przez środek rzutów O i równoległą do płaszczyzny terenu T.
W celu wyznaczenia linii i punktów charakterystycznych poprowadzimy przez środek rzutów O płaszczyznę β, zawierającą promień główny (oś zdjęcia 00' = f ) i prostopadłą do płaszczyzny terenu T. Krawędź przecięcia płaszczyzny β i π utworzy linię charakterystyczną zdjęcia, nazywaną główną pionową zdjęcia v' v'. Jest ona jednocześnie linią największego spadku płaszczyzny zdjęcia π.
Krawędź przecięcia płaszczyzny T z płaszczyzną zdjęcia π jest nazywana linią horyzontu zz. Stanowi ona jednocześnie ślad zbiegu płaszczyzny terenu T. Prowadząc przez punkt główny zdjęcia O' prostą równoległą do linii horyzontu otrzymamy główną poziomą zdjęcia h' h', która jest prostopadła do głównej pionowej zdjęcia. Punktami szczególnymi zdjęcia lotniczego są:
• punkt główny zdjęcia O',
• punkt nadirowy zdjęcia N',
• punkt izocentryczny zdjęcia f',
• główny punkt zbiegu Z'.
Punkt główny zdjęcia O' jest rzutem prostokątnym środka rzutów O (głównego punktu obiektywu) na płaszczyznę zdjęcia. Ma on duże znaczenie praktyczne jako punkt wyjściowy w pomiarach fotogrametrycznych.
Punkt nadirowy zdjęcia N' jest punktem przebicia płaszczyzny zdjęcia prostą pionową, przechodzącą przez środek rzutu O. Punkt nadirowy nie odfotografowuje się na zdjęciach wykonanych zwykłymi kamerami lotniczymi. Jego położenie na zdjęciu można wyznaczyć sposobem analityczno-graficznym - na podstawie znajomości kąta nachylenia v i ogniskowej kamery f. W tym celu rozpatrzmy zależności w ∆OO'N' (rys):
![]()
gdzie O'O = f, stąd odległość punktu nadirowego od punktu głównego mierzona wzdłuż prostej największego spadku wynosi:
O'N' = ftgv
Punkt nadirowy N' jest punktem zbiegu wszystkich linii pionowych, a więc linii prostopadłych do płaszczyzny terenu T.
Punkt izocentryczny zdjęcia I' jest punktem przebicia płaszczyzny zdjęcia π prostą, dwusieczną kąta nachylenia zdjęcia v. Punkt izocentryczny nie odfotografowuje się na zdjęciach, a położenie jego można jedynie wyznaczyć metodą analityczno-graficzną, na podstawie następującej zależności (rys):
![]()
gdzie O'0 = f, zatem
![]()
Powyższy wzór pozwala na obliczenie odległości punktu izocentrycznego I'od punktu głównego O'. Odległość tę odmierzamy wzdłuż głównej pionowej zdjęcia (prostej największego spadku). Szczególną właściwością punktu izocentrycznego jest to, że kąty, których wierzchołki znajdują się w tym punkcie, mierzone w płaszczyźnie zdjęcia, są równe odpowiednim kątom mierzonym w terenie, natomiast kąty mierzone w innych punktach zdjęcia nachylonego nie odpowiadają kątom rzeczywistym, ponieważ są obarczone błędem, wynikającym ze zmienności skali zdjęcia.
Główny punkt zbiegu - Z' - to punkt przebicia płaszczyzny zdjęcia prostą prostopadłą do linii horyzontu zz i przechodzącą przez środek rzutów O. Punkt ten leży na głównej pionowej zdjęcia v'v'. Odległość głównego punktu zbiegu Z' od punktu głównego zdjęcia O' można wyznaczyć sposobem analityczno-graficznym, znając kąt nachylenia zdjęcia v. Z trójkąta OZO' (rys) wynika zależność:
![]()
gdzie 0'O=f,
stąd 0'Z = f*ctgv
Główny punkt zbiegu Z' stanowi punkt zbiegu wszystkich linii terenu, które są równoległe do prostokątnego rzutu osi zdjęcia na płaszczyznę terenu T.
Odległość głównego punktu zbiegu Z' od środka rzutów O jest wykorzystywana praktycznie w procesie przetwarzania zdjęć lotniczych na przetwornikach fotomechanicznych. Odległość tę można wyznaczyć ze związków zachodzących w trójkącie 00'Z', gdzie:
![]()
ponieważ O'Z' = f*ctgv,
![]()
25. OBRÓT ZDJĘCIA W PŁASZCZYŹNIE I PRZESTRZENI - MACIERZE OBROTU „DUŻA” I „MAŁA”
1.Obrót w płaszczyźnie
- wlaność macierzy obrotu R
- odwrotność macierzy obrotu R-1
własności:
- macierz obrotu R jest macierzą ortogonalną
- suma kwadratów elementów w wierszu lub kolumnie =1
- odwrotność macierzy R= jej transpozie (dzięki temu, że jest to macierz ortogonalna) R-1=RT
2.Obrót w przestrzeni
- W odniesieniu do x,y,z,
29. ZALEŻNOŚĆ ZNIEKSZTAŁCEŃ OBRAZU ZDJĘCIA LOTNICZEGO OD DENIWELACJI TERENU.
Deniwelacje terenu powodują radialne (w stosunku do punktu nadirowego N) przesunięcie obrazów punktów położonych powyżej lub poniżej płaszczyzny odpowiadającej średniej wysokości terenu T. W rezultacie punkty terenu A i B, których rzut ortogonalny na płaszczyznę T odpowiednio A0 i B0 odfotografowują się na zdjęciu jako punkty A' i B'. Położenie tych punktów należy więc skorygować o wartość Δr, doprowadzając do położenia A'0 i B'0. W przypadku punktu A, który leży poniżej płaszczyzny T, korekta będzie polegała na przesunięciu jego położenia o wielkość r'A w kierunku od punktu nadirowego, natomiast w przypadku punktu B, leżącego powyżej płaszczyzny T, na przesunięciu położenia o odcinek r'B skierowany do punktu nadirowego.
W celu wyznaczenia wielkości odchyłki Δr'B rozpatrzymy zależności na rysunku a. Z podobieństwa trójkąta BB1B0 wynika proporcja:
![]()
ponieważ ΔrB = Δr'Bm
gdzie:
m - mianownik skali zdjęcia, stąd:
![]()
a zatem
![]()
lub ![]()
gdzie: Δr'B - odchyłka (przesunięcie liniowe) położenia punktu B' spowodowana deniwelacją terenu,
r'B - odległość korygowanego punktu od punktu nadirowego lub od punktu głównego zdjęcia prawie pionowego, Δh - różnica wysokości punktu terenu w stosunku do płaszczyzny odniesienia T, H - wysokość fotografowania (w odniesieniu do płaszczyzny T).
Jak wynika z powyższego wzoru, wpływ deniwelacji terenu na położenie obrazu punktu Jest tym większy, im bardziej jest on oddalony od punktu nadirowego, im większe jest przewyższenie tego punktu w stosunku do średniej wysokości terenu oraz im mniejsza jest wysokość fotografowania. Minimalne zniekształcenia występują w przypadku terenów równinnych i w środkowej części użytecznego pola zdjęcia.
Należy zaznaczyć, że praktycznie, w przypadku zdjęć prawie pionowych, poprawkę r'B odkładamy na promieniu Δr'B wykreślonym z głównego punktu zdjęcia O', gdyż prawie pokrywa się on z punktem nadirowym N'. Wpływ tej nieścisłości na ostateczne położenie punktu jest znikomy i nie przekracza granic dokładności graficznej.
30. ZALEŻNOŚĆ ZNIEKSZTAŁCEŃ OBRAZU ZDJĘCIA LOTNICZEGO OD KĄTA NACHYLENIA ZDJĘCIA.
Odchylenie osi kamery lotniczej od pionu w momencie fotografowania (nachylenie zdjęcia) powoduje przesunięcie obrazu punktów, a w konsekwencji perspektywiczne zniekształcenie obrazu fotografowanego terenu.
W celu wyznaczenia wielkości przesunięcia obrazu punktu terenu A" na zdjęciu nachylonym (Z2) w stosunku do położenia na zdjęciu pionowym (Z1) należy przeanalizować zależności geometryczne między tymi zdjęciami, zakładając że zostały one wykonane z tego samego punktu O, oraz że płaszczyzny ich przecinają się wzdłuż prostej poziomej, przechodzącej przez punkt izocentryczny I' (rys a). Prostą zbiegu płaszczyzny Z1 w stosunku do płaszczyzny Z2 jest prosta w"w", natomiast punktem zbiegu - punkt W", odległy od środka rzutu o wielkość
![]()
Odcinek ten można określić jako promień obrotu środka rzutów. Przez punkt A' na zdjęciu Z1 poprowadzimy prostą równoległą do głównej pionowej v'v'. Przetnie ona linię poziomą h"1 h"1 w punkcie D'. Prostej A'D" odpowiada prosta D'W" w płaszczyźnie zdjęcia nachylonego Z2. W przecięciu tej prostej z promieniem rzutującym punkt A otrzymamy jego obraz A".
Dokonując obrotu płaszczyzny Z2 wokół osi h"1 h"1, aż do pokrycia z płaszczyzną Z1, otrzymamy sytuację geometryczną jak na rysunku b.
Przyjmując punkt I' za początek układu współrzędnych biegunowych, a prostą h''1 h''1 za kierunek początkowy, możemy oznaczyć współrzędne biegunowe rzutów punktu A następująco:
A'(r'A , φ'A)
A''(r''A , φ''A)
Oczywiste jest, że kąt φ'A = φ''A natomiast wielkość odpowiadająca różnicy długości promienia:
r'A- r''A = Δr''A
jest szukaną odchyłką (przesunięciem liniowym) położenia rzutu punktu, spowodowaną nachyleniem kamery (w dalszych rozważaniach oznaczono ją jako Δrv).
Z podobieństwa trójkątów I' W'' A'' oraz A'D'A" wynika proporcja:
![]()
Po wprowadzeniu odpowiednich wartości odcinków otrzymamy: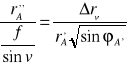
ale
r'A = r''v ,
stąd
skanery |
Format cm/cm |
Geometria zdj. piksel/cal |
Zdolnośc rozdzielcza |
DTP |
DIN A4/13 |
400-1200 |
8 bit (x3) |
Skanery mapowe |
60/90 |
400-1200 |
8 bit (x1-3) |
Skanery do zdjęć lotniczych |
26/26 |
3500 |
8 bit (x3) |
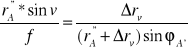
a po przekształceniu:
Δrv(f - r''Asin v * sin φ) = r''Asin v * sin φ
zatem ostatecznie
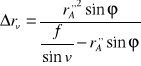
Powyższy wzór pozwala na obliczenie wartości odchyłki liniowej położenia punktu, spowodowanej nachyleniem zdjęcia. Wartość odchyłki jest minimalna (Δrv → 0) w przypadku, gdy punkt znajduje się na linii h'1h'1 lub w jej pobliżu (α = O, f/sin v → oo) oraz w przypadku bardzo małych wychyleń kamery (v → 0). Maksymalne wielkości zniekształceń występują w pobliżu linii horyzontu w"w"(φ→90°, r''A max, Δrv ± 00). Ogólnie, odchyłka Δrv, uwarunkowana nachyleniem osi optycznej kamery, powoduje zniekształcenia regularne o rozkładzie radialnym w stosunku do punktu izocentrycznego. Podobnie jak i odchyłka Δrh powoduje ona zniekształcenia odległości mierzonych na nachylonych zdjęciach lotniczych. W praktycznych obliczeniach odchyłki Δrv, gdy kąt nachylenia kamery v < 10°, stosuje się często wzór uproszczony:
![]()
W takim przypadku punkt izocentryczny zdjęcia można utożsamiać z punktem głównym, a błąd położenia punktu, wynikający z nachylenia osi kamery, eliminować w kierunku radialnym w stosunku do głównego punktu zdjęcia, odkładając poprawki w kierunku punktu głównego, gdy Δrv ma wartość dodatnią, bądź w kierunku od głównego punktu zdjęcia, gdy Δrv ma wartość ujemną. Znak odchyłki Δrv można ustalić obliczając skalę zdjęcia na przeciwległych jego krańcach. W tej części zdjęcia, gdzie skala jest mniejsza odchyłka Δrv ma wartość ujemną, natomiast tu gdzie większa - wartość dodatnią.
Zakładając określoną wielkość Δrv (wynikającą na przykład z technicznych warunków opracowania) można wyliczyć promień okręgu, w granicach którego przesunięcia liniowe punktów, wynikłe z nachylenia zdjęcia, nie będą przekraczały założonej wielkości. Obliczenie wykonujemy według wzoru:
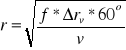
gdzie: f- ogniskowa kamery lotniczej, v - kąt nachylenia osi kamery od pionu (w stopniach), r - promień okręgu, w granicach którego zniekształcenia położenia punktów są mniejsze od Δrv.
Z powyższych rozważań wynika, że na położenia punktów na zdjęciu lotniczym wpływa zarówno nachylenie zdjęcia w momencie fotografowania, jak i rzeźba fotografowanego terenu. Łączny wpływ tych czynników powoduje, że błędy w położeniu punktów bądź sumują się, bądź też redukują. W związku z tym, jeśli nie ma możliwości uwzględniania wpływu tych czynników i wprowadzenia odpowiedniej poprawki, należy przy pomiarze odległości na podstawie zdjęć lotniczych wykorzystywać przede wszystkim ich część środkową, zwaną powierzchnią użyteczną, gdzie wpływ nachylenia zdjęcia i rzeźby terenu jest najmniejszy. Wielkość promienia powierzchni użytecznej zdjęcia można określić każdorazowo, stosownie do założonej maksymalnej wartości odchyłki sumarycznej, spowodowanej deniwelacją terenu i nachyleniem osi kamery:
Δrvh = Δrv + Δrh
Podstawiając przytaczane już wyrażenia, otrzymamy:
![]()
Wielkość promienia powierzchni użytecznej zdjęcia obliczyć można na podstawie wzoru:
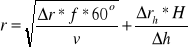
gdzie człon pierwszy wyraża dopuszczalną wielkość promienia ze względu ma odchylenie osi kamery, a człon drugi ze względu na deniwelację terenu odfotografowanego na zdjęciu.
Należy nadmienić, że zdjęcia lotnicze o kącie nachylenia v < 3°, obejmujące teren o deniwelacjach w granicach 80 m, mogą być wykorzystywane do celów interpretacji geograficznej bez konieczności wprowadzania korekty zniekształceń.
31. WYZNACZENIE ŚREDNIEJ SKALI ZDJĘCIA
- przy znajomości Ck i wys. lotu W
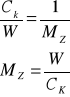
- gdy nie dysponujemy takimi samymi danymi wówczas musimy mieć mapę topograf. i porównujemy odcinki wyznaczane na zdj. Z tymi z mapy. One powinny być zorientowane wzdłuż prostych najw. spadku i gł. poziomej zdj. Wtedy:
![]()
D-dł odcinka z mapy topograf.
d-dł. odc. na zdjęciu
32. PRZEKSZTAŁCENIE RZUTOWE ZDJĘCIA NA PŁASZCZYZNĘ TERENU
Przekształcenie płaszczyzny obiektu (zdjęcia) XY (Z=0) uz płaszczyzna terenu . Wychodząc z równań warunku kolinearności po kolejnych przekształceniach otrzymujemy równania wiążące współrzędne tłowe ze wsp terenowymi (8 współczynników) ![]()
![]()
Dla takiego opracowania sytuacyjnego musimy mieć minimum 4 F pkt, aby wyznaczyć współczynniki transformacji. Każdy F pkt o znanych współrzędnych terenowych pomierzonych współrzędnych tłowych daje 2 równania.
33. TYPY SKANERÓW I ZASADA DIGITALIZACJI OBRAZU.
Typy skanerów
- mapowe - bębenkowe lub z linijką CCD
- skanery do zdjęć lotniczych
Ze względu na okres rejestrowanego promieniowania
- termalne (lub działające w podczerwieni) skanery liniowe (długa podczerwień)
- wielospektralne (widzialna i termalna część widma)
Ze względu na sposoby działania wyróżniamy skanery
- optyczno-mechaniczne - dokonują rejestracji terenu linią po linii - każdy piksel jest kolejno rejestrowany
- elektrooptyczny - równoczesna rejestracja wszystkich pikseli należących do jednej linii
Skanery
- kanałowe - posiada jeden detektor
- wielokanałowe - posiada 2 lub więcej detektorów
- skanery elektroopty. pow. CCD - zamiast linijki detektorów jest dwuwymiarowa matryca obr. CCD zaw. M linijek czyli N*N detektorów
Dygitalizować - uzyskiwać z analogowej reprezentacji wielk. fizycznej zbliżone wielkości w postaci cyfrowej
Skanery fotogram i skanowanie zdjęć
34. OBRAZ CYFROWY?
Jest to uporządkowany zbiór pikseli w postaci np. macierzy z przypisanymi do nich jasnościami spektralnymi lub poziomami szarości zapisanymi na nośniki danych najczęściej na stronę bajtową tzn. stopień szarości pojedynczego piksela jest opisywany cyfrowo w granicach 0 (czerń) do 2 55 (biel) tg 28 = 256 poziomów szarości, położenie piksela w obrazie oznaczają rzędy i kolumny macierzy tj. wsp. płaskie obrazu.
*zbiór odpowiedzi spektralnych uporządkowany,pomierzony na elementernych polach obiektu i zapisany komputerowo.
Cechy:
1)geometryczne-rozdzielczość(dpi-liczba pikseli na cal=25,4mm);wielkość matrycy obrazu(liniowo 5x5,kolumny i wiersze);wymiar piksela;uklad wspol. Pikselowych w lewym gornym rogu
2)radiometryczne-sposób zapisu obrazu odpowiednią liczbą bitów(6,8,24,32 bity);jasność i kontrastowość obrazu cyfrowego
3)spektralne-rejestracja może dotyczyć określanego ,wspolnego zakresu fal elektromagnetycznych
35. DYSKRETYZACJA I KWANTYZACJA (ZAPIS OBRAZU CYFROWEGO)
Dyskretyzacja - przedstawienie obrazu w określonej liczbie pikseli. Mówi o tym w ilu pikselach został zapisany dany obraz.
Kwantyzacja - przypisanie odpowiednim pikselom których położenie jest już zidentyfikowane w matrycy odpowiednich poziomów szarości. Obraz powinien być kwantyzowany przy jak największej liczbie k.
36. UKŁAD WSPÓŁRZĘDNYCH PISELOWYCH.
standardowo może być zdefiniowany tak, że początek układu współrzędnych jest w lewym górnym rogu matrycy
- jest prostokątny to trzeba uwzględnić jego wymiar przy przejściu od układu współrzędnych pikselowych na układ tłowy
Przejście z jednego układu do drugiego
x'=(x'-x'p)*psx
z kładu pikselowego do tłowego
y'=(y'p-y')*psy
psx-wymiar piksela wzdłuż osi odciętych
37. CECHY OBRAZU CYFROWEGO
Geometryczne - rozdzielczość powierzchniowa-wymiar piksela w terenie
określają geometrię obrazu
wymiar obrazu.
Liczbę pikseli na cal
Wymiar pxl
Układ wsp. pxl w lewym górnym narożniku
Radiomatyczne - rozdzielczość radiomatyczna-opisuję zasięg oraz dająca się wyróżnić liczbę określającą dyskretne wartości jasności
6 bit, 8 bitowy, 24 bit, 32 bi-czyli ilość bitów potrzebnych do zapisania obrazu cyfrowego
jasność obrazu cyfrowego
kontrastowość obrazu cyfrowego
Spektralne - rejestracja może dotyczyć określanego wspólnego zakresu fal elektromagnetycznych.
38. ANALIZA OBRAZU CYFROWEGO - HISTOGRAM OBRAZU
Histogram obrazu cyfrowego-jest to określenie z jaką częstotliwością występują piksele o określonym poziomie szarości. Przedstawiony w postaci wykresu, tabel (jest to statystyczny rozkład skali szarości w funkcji liczby pikseli)
Możemy go zmienić:
przez zastosowanie procesu wyrównania - histogram sprawdzamy przy wyrównaniu do stanu gdy częstotliwości występowania pikseli o podobnym stopniu szarości jest jednakowa. Zmienne są wartości poziomu szarości przypisane każdemu pikselowi
normalizacja histogramu - histogram jest sprawdzany do krzywej Gaussa - rozkład częstotliwości odpowiada krzywej Gaussa.
METODY POPRAWIENIA JAKOŚCI OBRAZU CYFROWEGO
- sprowadzenie ...... do krzywej Gaussa
- wyrównanie histogramu zakładamy pewien poziom szarości do wyrównania
- rozciągnięcie histogramu - poprawienie kontrastu;
- filtracja obrazu - np. w celu wyeliminowania szumów.
Interpretacja przez histogram:
obraz ciemny
b) obraz jasny
c) obraz kontrastowy
d) obraz małokontrastowy
40. FILTRACJA OBRAZU CYFROWEGO - RODZAJE FILTRÓW I ICH ZASTOSOWANIE.
Filtrowanie - ma na celu polepszenie jakości zdjęcia.
Przyczyny pogorszenia jakości obrazu:
zakłócenie w transmisji danych cyfrowych pracy sensora;
zła ostrość;
dodatkowe szumy;
błąd sensora.
Metody filtracji:
przestrzenne i częstotliwościowe.
liniowe i nieliniowe.
Najpopularniejszy podział filtrów:
dolnoprzepustowe - do eliminacji szumu na skutek digitalizacji, defektu poziomu szarości na skutek błędu szarości kamery - wygładzają szczegóły w obrazie, zmniejszają poziom kontrastu obrazu cyfrowego ( rozmazanie i nieostrość krawędzi), wygaszanie wysokich częstotliwości.
górnoprzepustowe - wzmacniają krawędzie i wyodrębniają ostre zmiany intensywności w obrazie, tłumi niskie częstotliwości.
środkowoprzepustowe - najrzadziej stosowane ( do wyodrębniania określonych szczegółów).
Filtry
obraz cyfrowy reprezentowany jest przez 3 wymiar ( wsp. pikselowe x, y i poziom szarości)
filtrem jest macierz o określonych wartościach przez które mnożymy obraz wyjściowy ( pierwotny)
Wyznaczana jest nowa wartość
wsp. 
jest to filtr uśredniający
filtrowanie jest procesem stratnym, bo ostatnia kolumna i ostatni wiersz po filtrowaniu są czarnymi pasami ale dzięki funkcji ob. cyfr. jest to eliminowane ;
filtr uśredniający - tłumaczenie częstotliwościowych zakłóceń oraz tłumaczenie poziomów szarości dla krawędzi o wysokim poziomie szarości - ten filtr ma małe znaczenie, średnia wartość z przedziału zmniejsza błędy, zmniejsza ostrość krawędzi;
gdy zakłócenie obejmuje pojedynczy piksel to możemy zastosować filtr:

- gdy zakłócenie jest linią poziomą to stosujemy filtr:

- gdy zakłócenie jest linią pionową to stosujemy filtr:

41. METODY INTERPOLACJI OBRAZU CYFROWEGO.
algorytmy zmieniające poziom szarości danego piksela w odpowiedni dla jego otoczenia ( interpolacja powoduje wygładzenie obrazu - przechodzimy ze strony pikselowej do półtonowej)
metoda najbliższego sąsiada - zaokrąglana jest współrz. danego piksela do najbliższego pełnego piksela ( piksel przejmuje jasność od najbliższego sąsiada)
bilinearna - realizowane jest sąsiedztwo 4 najbliższych pikseli. Nowy piksel ma nowy poziom szarości wynikający z 4 sąsiadujących pikseli (nie jest to śr. arytmetyczna )
bikubiczna - piksel otrzymuje nowy poziom szarości wynikający z sąsiednich 16 pikseli (4x4)
42. PIRAMIDY OBRAZÓW.
Piramida jednokrotna - obraz pierwotny zdegradowany
( została zmniejsz. Dla jego rozdzielczości)
Piramida obrazów - stopniowo zmniejsza się rozdzielczość obrazu pierwotnego, by uzyskać szybkość wyświetlania i pozycjonowania obrazów, Schemat:
3 2
6 4
1 2 8
2 5 6
proces tworzenia piramidy obrazu - hierarchiczna wielopoziomowa korelacja;
machting - dopasowanie obrazów
Metody tworzenia obrazów piramidalnych -służą do przyspieszania procesu pomiarowego i szybszego wyznaczania położenia obiektów:
* wysuwamy z obrazu pierwotnego co drugi wiersz i co drugą kolumnę obrazu cyfrowego;
* uśredniamy wartości sąsiednich wierszy i kolumn obrazu cyfrowego;
* zastosowanie jednej z czterech metod interpolacji;
* metody związane z wygładzaniem.
45. FIZJOLOGICZNE PODSTAWY STEREOSKOPOWEGO WIDZENIA.
Każde oko zajmuje inne położenie w przestrzeni i obrazy powstałe w każdym oku są różne. Właściwość kojarzenia takich dwoch obrazów w jeden obraz przestrzenny nazywamy zdolnością widzenia stereoskopowego. Widzenie takie, które jest niejako wcięciem w przód, umozliwia ocenę przedmiotów we wszystkich trzech wymiarach, a także pozwala oceniać odległości.
najdłuższa odległść R, przy której można jeszcze odróżnić położenie punktów dotyczące uszeregowania w głąb nazywamy promieniem nieuzbrojonego widzenia stereoskopowego jest on dla rozstawu oczu b0 = 65 mm, ostrości stereoskopowegowidz. ustalonej doświadcz. γ = 30'' wynosi Rmax (b0/γ)*Q = 450 m
minimalny kąt widzenia w płaszczyźnie pionowej wynosi 1500 , a w poziomej 1200,
120 mln prążków w oku reaguje na światło, ale nie rozpoznaje barw
plamka żółta posiada największą czułość;
punkt ślepy - przyczepiony do nerwu wzrokowego;
paralaksa - różnica odległości Pi'P' oraz Pi''P'';
akomodacja - zdolność oka do widzenia ostro w różnych odległościach;
rozdzielczość dla obserwacji monokularnych -1min., dla obserwacji dwóch linii 5-10 sek
widzenie stereoskopowe δi = γ-γi to jest równoznaczne z powstaniem różnicy, czyli paralaksy pi = Pi'P' - Pi''P''
paralaksa fizjologiczna waha się od 17-50 s, min. 10-25 sek.
Zdolność rozdzielcza ( przy odległości dobrego widzenia 250 mm) wynosi 0,07 mm
46. METODY OTRZYMYWANIA EFEKTU STEREOSKOPOWEGO
1. Sposób optyczny
Polega on na rozdzieleniu promieni biegnących od lewego zdjęcia do lewego oka i promieni biegnących od prawego zdjęcia do prawego oka za pomocą specjalnych układów optycznych. Najprostszym układem optycznym służącym dla wymienionego celu jest stereoskop zwierciadlany.
2. Sposób anaglifowy
Polega na połączeniu dwóch obrazów, tego samego obiektu, zabarwionych dopełniającymi się kolorami i obserwacji ich przez filtry optyczne (barwne) tak dobrane, aby każde oko widziało tylko jeden obraz.
3. Sposób wirujących przesłon
Polega na przemiennym rzutowaniu obrazu lewego zdjęcia i prawego zdjęcia. Do przemiennego rzutowania używane są dyski z wyciętymi rowkami.
4. Sposób polaroidów
Podobny do sposobu anaglifowego, z tym, że dla rozdzielenia obrazów - zamiast kolorowych filtrów - stosowane są polaryzatory optyczne. Działanie tych polaryzatorów polega na uporządkowaniu drgań fal świetlnych w jednej wybranej płaszczyźnie.
5. Sposób rastrów
Polega na równoczesnym rzutowaniu dwu zdjęć poprzez siatki linii równoległych, co prowadzi nie tylko do uzyskania modelu stereoskopowego, ale także linii na tym modelu, które są odpowiednikami warstwic.
6. Sposób holograficzny
Różni się zdecydowanie od wszystkich metod możliwością bezsoczewkowego uzyskania modelu stereoskopowego za pomocą światła spójnego.
47. MODEL STEREOSKOPOWY - WARUNKI OPTYCZNE I GEOMETRYCZNE SZTUCZNEGO EFEKTU STEREOSKOPOWEGO WIDZENIA
Uzyskanie modelu stereoskopowego uzależnione jest od pewnych czynników:
Czynniki związane z procesem fotografowania:
Wykonanie zdjęć z dwóch różnych punktów przestrzeni (baz fotografowania) - podobna odległość od obiektu,
Różnica skal między zdjęciami nie może przekraczać 15%)
Kąt pod, którym obserwowane są obrazy nie może być większy od 15º.
Pokrycie podłużne zdjęć 60%, poprzeczne 20 - 40%.
Czynniki ograniczające uzyskanie efektu stereoskopowego:
Konieczność prowadzenia obserwacji punktów modelu stereoskopowego w płaszczyznach rdzennych
Prowadzenie obserwacji zdjęć z odległości najlepszego widzenia
Odpowiednie ułożenie zdjęć do obserwacji (zdjęcie lewe stereogramu powinno być obserwowane lewym okiem, a prawe zdjęcie - prawym
max format zdjęć 18*18 cm
pomiar x', y', Px, Py
dokładność pomiaru współrzędnych tłowych ok. 10M m
znaczek pomiarowy wyobrażalny
max format 24*24 cm
dokł. ok. 3M m
pomiar x', y', Px, Py
transformacja przez podobieństwo (konforemna) transformacja Helmerta - zachowuje kąty w skali. Mamy do wyznaczenia 4 wsp, które opisują nam model korekcji tak, że musimy mieć 2 znaczki tłowe z pomierzonymi wsp tłowymi z uwzględnieniem kalibracji kamery. Możemy wtedy ułożyć 4 równania obserwacyjne rozwiązać je metodą podstawienia i wyznaczyć niewiadome: a0, b0, a, b. Zakładamy tu, że: osie układu są ortogonalne, zniekształcenia skali wzdłuż obu osi są jednakowe (2 pkt dostosowania)
Po bazie
Poprawne ułożenie negatywów lub diapozytywów na płytce szklanej (nośniki zdjęć), krzyżyki wyznaczają środki obrotów - punkty główne zdjęć
Za pomocą pokrętła x i y sprowadzamy lewy znaczek pomiarowy na pkt główny lewego zdjęcia
Posługując się pokrętłami x, p, q naprowadzamy znaczek pomiarowy na pkt główny prawego zdjęcia (wtedy ucieka lewy pkt główny)
Pokrętłem x naprowadzamy lewy znaczek pomiarowy na lewy pkt główny
Pokrętłem p w polu widzenia okularu naprowadzamy szczegół sytuacyjny
Po znaczkach tłowych
Pokrętłami x i y naprowadzamy lewy znaczek pomiarowy na pkt główny lewego zdjęcia
Pokrętłem x naprowadzamy znaczek tłowy nr 6 lub 8, widoczną paralaksę usuwamy pokrętłem (kappa)
Kontrolę poprawności orientacji przez powrót na lewy pkt główny
Wszystkie czynności powtarzamy dla prawego zdjęcia wykorzystując tylko prawą część układu optycznego
w punkcie a usuwa się paralaksę py przesuwem by''
1 - obrót κ''
4 - przesunięcie bz'' [ωL, φL, κL]
3 - obrót φ''
6 - nadkorekcja paralaksy obrotem ω''
powtórka czynności od 1 - 5 dopóki paralaksa nie zniknie na 5 punktach orientacji
kontrolę orientacji przeprowadza się punktem 5. Jeżeli występuje tam paralaksa tzn że nie usunięto jej dokładnie na poprzednich punktach.
ze znanych lub przyjętych dla pierwszego zdjęcia obrotów tworzymy macierz obrotów A i określamy następujące wielkości x', y', z', współrzędne wektora r'.
wybieramy wartości przybliżone dla drugiego zdjęcia 1by, 1bz, 1φ'', 1ω'', 1χ''.
obliczamy wartości 1x', 1y', 1z' za pomocą wartości z punktu 2.
obliczamy niewiadome dφ, dω, dχ, dbz, dby przez rozwiązanie minimum 5 równań.
obliczamy elementy pierwszej poprawionej macierzy 2A posługując się elementami obliczonymi w punkcie 4.
obliczamy macierz A=2A*1A. Elementy tej macierzy posłużą do obliczeń jak w punkcie 3.
powtarzamy obliczenia od punktu 3 do 6 dopóki dφ, dω, dχ, dbz, dby nie staną się dostatecznie małe aby je pominąć.
naturalna sygnalizacja (do opracowań map średnio i małoskalowych)
sygnalizowane sztucznie - przed nalotem
skali zdjęć
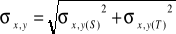
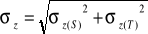
2D opracowanie
mierzymy współrzędne tłowe (x', y')
na ich podstawie i fotopunktów (min 4) wyznaczamy współrzędne X, Y w terenie
3D opracowanie np. aerotriangulacji
co najmniej 2 zdjęcia,
mierzymy na nich x', y', x'', y'',
musimy mieć też min 3 fotopunkty otrzymujemy X, Y, Z terenowe (geodezyjne)
istnieje możliwość dołączenia obserwacji geodezyjnych (np. pomierzonych długości między fotopunktami, obserwacji różnic wysokości, pomierzone azymuty, pomierzone kierunki) co czyni układ równań lepiej rozwiązywalnym,
można przyjąć do wyrównania obserwacje fikcyjne np. obserwacje zbiornika wodnego, przyjmujemy że powierzchnia wody jest w każdym punkcie taka sama,
możemy też wprowadzić dodatkowe parametry opisujące błędy systematyczne zdjęcia (dystorsja radialna, tangencjalna, deformacja negatywu). Można je opisać w postaci wielomianu
najdokładniejsza metoda rozwiązania aerotriangulacji dzięki temu, że zachodzi bezpośredni związek między współrzędnymi zdjęcia a współrzędnymi geodezyjnymi, wyrównanie przez równanie kolinearności (nie ma konieczności rozwiązania pojedynczego modelu jako etapu obliczeń)
jest możliwość wprowadzenia dodatkowych obserwacji geodezyjnych,
możliwość prowadzenia obserwacji GPS dla EOZ,
wprowadzenie obserwacji fikcyjnych (obserwacje np. punkty leżące na jednej prostej - linia przesyłowa wysokiego napięcia na wybranym odcinku),
możemy wprowadzić parametry dodatkowe opisujące błędy systematyczne kamery????????????????????????,
pozwala wyznaczyć obraz rastrowy dla autografów analitycznych i cyfrowych (bo otrzymujemy EOZ zdjęć),
pozwala rozwiązać zdjęcia o niekonwencjonalnych orientacjach
optyczno - mechaniczne urządzenie systemu projekcji,
komputer sterujący,
komputer aplikacyjny - funkcja kreślenia,
2 wózki, nośniki zdjęć,
komputer sterujący (transformacja w czasie rzeczywistym z układu współrzędnych zdjęcia do układu współrzędnych modelu - transformacja m' x(X) numeryczna
48. RODZAJE EFEKTU STEREOSKOPOWEGO
W zależności od ułożenia zdjęć względem siebie może być uzyskany jeden z trzech rodzajów efektu stereoskopowego:
- efekt ortoskopowy - przy którym model utworzony z pary zdjęć lotniczych ma ukształtowanie pionowe zgodne z naturalnym tzn. wzniesienia terenowe są skierowane w stronę obserwatora. Bazy fotografowania zajmuje położenie „do wewnątrz”.
- efekt pseudoskopowy - przy którym następuje zmiana ukształtowania pionowego, tzn. formy wypukłe obserwyje się jako wklęsłe, rzeki płyną grzbietami itp. Powstaje na skutek obserwacji zdjęcia lewego prawym okiem, a prawego lewym. Baza fotografowania na zdjęciach zajmuje położenie „na zewnątrz”.
- efekt zerowy - (minimalny), przy którym zanika wrażenie plastyki. Teren płaski. Zdjęcie lewe skręcone jest o 90o i obserwowane lewym okiem, a prawe jest także skręcone o 90o i obserwowane prawym okiem. Efekt zerowy stosowany jest wtedy, gdy przy obserwowaniu stereogramu niepożądana jest obserwacja przestrzennego ukształtowania terenu.
49. WIRTUALNY ZNACZEK POMIAROWY
Sposób pomiaru za pomocą znaczka wirtualnego nazywany jest także sposobem dwóch znaczków rzeczywistych wyobrażalnego. Ogólną zasadą pomiaru stereoskopowego za pomocą dwóch znaczków wyjaśnia rysunek. Jeżeli w polu widzenia każdego zdjęcia umieścimy znaczek pomiarowy, którego położenie względem zdjęcia może się zmieniać, to istnieje takie jedno położenie znaczka, przy którym jest on styczny do powierzchni modelu.
W położeniu wyjściowym - stosunkowo łatwo jest monokularne pokrycie jednego znaczka pomiarowego z obserwowanym punktem, np. a'. Równocześnie z tym drugi znaczek przemieszczany jest w płaszczyźnie drugiego zdjęcia (π2). Jeżeli ustawienie drugiego znaczka odpowiada położeniu 3, to przestrzenny znaczek pomiarowy znajdzie się pod powierzchnią widocznego modelu stereoskopowego. Dopiero dokładne naprowadzenie prawego znaczka na punkt a'' zdjęcia π2 - położenie 1 - prowadzi do styczności wyobrażalnego znaczka pomiarowego z mierzonym punktem A modelu. Doprowadzenie do styczności wyobrażalnego znaczka pomiarowego z obserwowanym punktem modelu, osiągnięte więc jest poprzez dokładne naprowadzenie znaczków rzeczywistych na jednoimienne punkty zdjęć π1 i π2. następnie na licznikach instrumentu wykonywane są odczyty położenia punktów na zdjęciach.
Wartość odczytu odpowiadającego położeniu znaczka pomiarowego na danym punkcie zdjęć jest funkcją tego punktu na powierzchni modelu stereoskopowego od bazy obserwacji.
50. INSTRUMENTY DO UPROSZCZONYCH OPRACOWAŃ STEREOFOTOGRAMETRYCZNYCH - STEREOSKOP ZWIERCIADLANY I STEREMIKROMETR.
Stereoskop zwierciadlany składa się z dwóch par luster, które ustawione są w stosunku do obserwowanych zdjęć pod kątem 45˚. Promienie biegnące od lewego zdjęcia widziane są jedynie lewym okiem, a promienie biegnące od prawego zdjęcia prawym okiem. Jeżeli obserwacje prowadzone są w płaszczyznach rdzennych, to obserwator odbiera efekt stereoskopowy modelu A, L, C. Model ten powstaje na przecięciach się przedłużeń promieni, jednoimiennych punktów, wpadających do oczu obserwatora. Baza obserwacji b0 zostaje powiększona do wielkości nb0, dzięki zastosowaniu rozstawionych zwierciadeł. W niektórych typach stereoskopów, oprócz zwierciadeł, umieszczone są także soczewki albo lunetki, których zadaniem jest dodatkowe powiększenie obrazu.
Stereomikrometr - śruba pararalaktyczna za pomocą, której mierzy się różnice paralaks. Składa się z 2 identycznych znaczków pomiarowych na płytkach szklanych, które ułożone na zdjęciu pod stereoskopem umożliwiają - za pomocą mikrometru - pomiar różnic paralaks.
53 STEREOKOMPARATORY - STEKOMETR 1818 I STEREOKOMPARATOR PRECYZYJNY STECOMETR C
„książka stereofotogrametria lotnicza2”M. Graliński str 39-46
stereokomparator- urządzenie do pomiaru współrzędnych tłowych lub paralaks stereogramu. Do pomiaru przyjnuje się równoległe pary zdjęć; układ odniesienia to oś „x” lub oś „y”, doprowadzany poziomą łącznicą lewego i prawego zdjęcia do równoległości z osią x stereokoparatora (lub pionową łącznicą do równoległości z osią y streokomp.).
Steco 1818
budowa: żeliwna rama z prowadnicami, po której przesuwa się wózek, licznik ze śrubą, zacisk dokujący, śruba „q” - do ustawiania paralaksy poprzecznej, „p”-paralaksy podłużnej, okulary, układ optyczny, włącznik oświetlenia.
Stecometr C
budowa: komputer, urządzenie do odczytu i transmisji danych, jednostka centralna: okulary o dużym powiększeniu, nośniki zdjęć na wózkach, korbki powodujące przesunięcie obydwu zdjęć (ruch „x”, lub ruchomych części układu optycznego - ruch „y”; korbki nośników zdjęcia prawego [Px=p] /prawe porusza się wzglllędem lewego/; korbki nośników zdjęci lewego [Py=q] /lewe porusza się wzglllędem prawego/) , 6 różnych znaczków pomiarowych.
54. CYFROWE EKRANOWE MONO I STEREOKOMPARATORY
VSD (videostereodigitizer) - cyfrowy autograf analityczny, może pracować jako monokomparator i jako stereokomparator. Pomiar odbywa się na ekranie monitora za pomocą znaczka pomiarowego (sterowanego myszą)
POPOS -dokładność porównywalna z dokładnością stereokomparatorów precyzyjnych rzędu ok. 0,1-0,3 piksela, monitor + odpowiednie oprogramowanie
56 REDUKCJA WSPÓŁRZĘDNYCH TŁOWYCH ZDJĘCIA I PIKSELOWYCH OBRAZU
x0,y0 - określa położenie środka rzutów w stosunku do układy współrzędnych tłowych na zdjęciu
(rys) xa = xa' - x0,
w procesie transformacji afinicznej dokonuje się redukcji współrzędnych tłowych i korekcja błędów systematycznych (min. 3 pkt dostosowania, najpierw odległość wsp. transformowanych, potem przeliczane są współrzędne)
(rys) przejście z układu pxl. do tłowego x' = (X' - Xp') px
x' = (Y' - Yp') py
Transformacja pomierzonych wsp pixelowych do układu wsp tłowych za pomocą transformacji afinicznej w VSD
Metody transformacji wsp tłowych zdjęcia i pxl obrazu
Deformacje spowodowane są tym, że nie zachowana jest oś odciętych, rzędnych przy skanerze. Otrzymujemy układ z nieprostopadłymi osiami, wówczas trzeba stosować transformacje, które powodują:
- redukcję układu
- wprowadzenie korekcji deformacji ze względu na błędy systematyczne podłoża fotograficznego (najczęstszym źródłem błędów systematycznych jest niedociskanie materiału fotograficznego w momencie ekspozycji oraz zniekształcenie spowodowane jego obróbką i przechowywaniem)
- największa jest deformacja materiału negatywowego
- błędy szczególne układu optycznego kamery fotograficznej (deformacja radialna i tangencjalna)
Do wprowadzenia korekcji systematycznych błędów wsp tłowych stosuje się następujące transformacje, które przekształcają pomierzone wsp tłowe na układ wsp wzorcowych
Sytuacja: mamy 4 znaczki tłowe i obserwując wsp tłowe jesteśmy w stanie ułożyć 8 równań:
x' = a0 + a1xs' - b1ys'
y' = b0 + b1xs' - a1ys' xs', ys' - w układzie stereokomparatora
2. pseudoafiniczna (bilinearna) - musimy wyznaczyć współczynnik, stąd potrzeba 4 znaczków tłowych. Stosowanie metod ścisłych jest utrudniona, ponieważ brak tu obs nadliczbowych, tzn układ równań jest słabo określony. Transformacja ta nie powinna być stosowana w przypadku kamer z 4 znaczkami tłowymi, jajlepiej stosować ją dla kamer semimetrycznych ... ponieważ tutaj jest dużo obs nadliczbowych.
x' = a0 +a1xs' + a2ys' + a3xs'ys'
y' = b0 + b1xs' + b2ys' + b3xs'ys'
3. afiniczna - zakłada wyznaczenie 6 współrzędnych opisujących ten model transformacji. Musimy tu mieć 3 znaczki tłowe i na ich podstawie ułożyć 6 równań poprawek dla współczynnika. Dzięki niej można obliczyć mx, my (wsp zmiany skali wzdłuż osi) oraz kąty między osiami układu. Metoda uwzględnia nieprostopadłość osi układu i różnoskalowe zniekształcenia wzdłuż osi układu wsp. Mimo że nie zachowuje kształtu, linie równoległe po transformacji pozostają równoległe. Oprócz poprawienia skurczu za pomocą wsp skalujących, transformacja poprawia również przesunięcie początku układu współrzędnych z układu wsp komparatora xs, ys do układu wsp tłowych zdjęcia x, y oraz stosuje obrót o kat skręcenia obydwu układów.
x' = a0 +a1xs' + a2ys' + a3xs'ys' => x' = x0 + Rx'
y' = b0 + b1xs' + b2ys' + b3xs'ys'
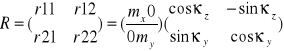
Etapy: I - określenie wsp a i b wykorzystując pkt, które znane są w obydwu układach
II - przeliczenie wszystkich pkt z układu xs, ys na układ x, y wykorzystując obliczone współczynniki. W celu wprowadzenia poprawek można napisać 2 równania typu (wyżej) dla każdego znaczka tłowego, czyli dla 4 znaczków tłowych 4 równania Mz współrzędnych x i 4 dla y. Dla określenia współczynnika a potrzeba tylko 3 równań dla wsp x, podobnie jak dla współczynnika b wystarczają 3 równania Mz wsp y. Dlatego równoczesne rozwiązanie tych równań met najmniejszych kwadratów zwiększa dokładność wyznaczanych niewiadomych.
57D WARUNEK KOLINEARNOŚCI
(rys)
Zdjęcie w położeniu pozytywowym
Wektor rb - wektor obrazowy wychodzący ze stanowiska naświetlenia zdjęcia D do pkt obrotu b
Wektor Rb - wektor przedmiotowy wychodzący ze stanowiska środka rzutów O do pkt przedmiotu B
Wektory te są kolinearne tzn jeden jest skalarny wielokrotnością drugiego, zatem rb = kaB i punkt przedmiotu B, środek rzutów O i pkt obrazu b leżą na jednej prostej. Warunek ten może być zakłócony, gdyż zniekształcenie obrazu spowodowane dystorsją obiektywu, refrakcją atm itp mogą spowodować odchylenie promienia od kolinearności - można je wyeliminować za pomocą poprawek
58. ANALITYCZNE WYZNACZENIE EOZ ZDJĘCIA - x0, y0, z0, ω, φ, κ
a) Wyznaczenie EOZ na podstawie przekształcenia rzutowego na podstawie odpowiednich wzorów , mając 8 pkt oraz interpretacyjnie
b) z warunku kolinearności (wcięcie wstecz) We wzorach warunku kolinearności występuje 9 niewiadomych x0, y0, Ck, Xs, Ys, fs, ω, φ, κ (5 fotopunktów) lub jeśli znane są EOW (3 F)
Jeśli EOW są znane i przyjmujemy przybliżone wartości EOZ i poprawki do nich to mając obserwacje nadliczbowe można ułożyć równania poprawek ( ) macierzowo w postaci V=AX-L L-macierz wartości stałych MIN. V - macierz poprawek wsp tłowych, A- macierz współczynników mij występujących przy niewiadomych.
Rozwiązanie układu równań metodą iteracyjną x - macierz niewiadomych poprawek do przyjmowania na początku wartości przybliżonych.
c) Przestrzenne wcięcie wstecz do wyznaczenia Xs, Ys, Zs mając 3 Fotopunkty. Porównuje się kąty α, β, γ określone odpowiednio równaniami zawarte między kierunkami do F pkt-ów w przestrzeni przedmiotowej i ich obrazów na zdjęciu . .. w przestrzeni obrazowej. Przyjmuje się przybliżone wartości Xs, Ys, Zs i iteracyjnie wyznacza poprawki do nich (dopóki poprawki nie staną się bliskie 0)
58A METODY ORIENTACJI ZDJĘĆ NA STEREOKOMPARATORACH
59. PARA ZDJĘĆ. ELEMENTY ORIENTACJI WZAJEMNEJPARYZDJĘĆ:
Δφ - różnica między kątami nachylenia podłużnego, określona w płaszczyźnie x2z2
Δω - różnica między kątami nachylenia poprzecznego, określona w płaszczyźnie y2f
Δκ - różnica między kątami skręcenia, określona w płaszczyźnie drugiego zdjęcia π''
![]()
Kąt nachylenia bazy względem przyjętego układu odniesienia ( oś pierwszego zdjęcia pionowa zatem płaszczyzna x1y1 pozioma )
![]()
Kąt zwrotu bazy w stosunku do przyjętego układu x1y1z1 dla pierwszego zdjęcia
88888888888888888888888888888888888888888888888
PIKSEL
Określenie piksel jest skrótem angielskiego wyrażenia określającego element obrazu (picture element). Piksel jest zatem najmniejszą częścią obrazu cyfrowego. Zobrazowania rastrowe mają strukturę siatki, której każda komórka reprezentuje piksel. Dlatego piksel często nazywany jest komórka siatki.
Piksel jest pojęciem o szerokim znaczeniu, używanym do określenia dwóch poniższych przypadków:
• wartości pliku danych - piksel określa pojedynczą wartość (radiometryczna - przyp. wyd.) danej na zobrazowaniu (piksele pliku - file pixels)
• miejsca oczka siatki na ekranie monitora lub na wydruku (piksel zobrazowania - display pixels)
Zazwyczaj jeden piksel w pliku odpowiada jednemu pikselowi na ekranie monitora lub na wydruku. Zobrazowanie może być jednak powiększane i zmniejszane, co powoduje, że jeden piksel pliku nie odpowiada już jednemu pikselowi zobrazowania lub wydruku. Na przykład, jeśli zobrazowanie jest wyświetlane ze współczynnikiem powiększenia równym 2, wtedy jeden piksel pliku zajmuje na ekranie monitora 4 (2 x 2) komórki siatki.
Wyświetlając obraz, piksel pliku reprezentujący jedną lub więcej wartości, musi zostać przetransformowany na piksel monitora w taki sposób, aby mógł być widoczny - muszą więc być przetworzone jego jasność i kolor. Ponieważ piksel pliku ma takie wartości, które odpowiadają danym (takim jak długość fali promieniowania odbitego), piksel wyświetlony na ekranie musi mieć określony kolor lub poziom szarości odpowiadający wartościom pliku danych.
60. WYZNACZENIE ELEMENTÓW ORIENTACJI WZAJEMNEJ- PRZYPADEK NIEZALEŻNEJ I ZALEŻNEJ PARY ZDJĘĆ
I) niezależna orientacja wzajemna przeprowadzana sposobem kolejnych przybliżeń wykorzystuje 6 pkt rozmieszczonych standardowo. Punkty te nazywane są punktami orientacji - pkt 1 i 2 są rzutami pkt lewego i prawego zdjęcia, a pkt 3, 4, 5, 6 leżą w czterech narożach modelu stereoskopowego w jednakowej odległości na prostych prostopadłych do łączącej punkty 1 i 2 (bazy modelu)
1) czynności przygotowawcze
2) usunięcie paralaksy podłużnej - zmianą wysokości ekranu stolika
3) eliminuje się paralaksę poprzeczną: - usuwa się paralaksę py w pkt 1 obrotem κ'' prawego projektora
- usuwa się paralaksę py w pkt 2 obrotem κ' lewego projektora
- usuwa się paralaksę py w pkt 3 obrotem φ'' prawego projektora
- usuwa się paralaksę py w pkt 4 obrotem φ' lewego projektora
- wprowadza się połowę występującej w pkt 5 lub 6 paralaksy py w kierunku przeciwnym jej występowaniu obrotem ω któregokolwiek projektora
- powtarza się czynności wyżej wymienione dopóki nie zostanie usunięta całkowicie paralaksa na tych 5 punktach. Szósty punkt służy do kontroli poprawności wykonania orientacji wzajemnej.
II) Zależna orientacja wzajemna jest wykorzystywana wtedy, gdy jeden z projektorów nie może zmieniać swojego położenia. Wówczas wykorzystuje się przesunięcia i obroty ω, φ, κ, by i bz tylko drugiego projektora. Najpierw dokonuje się eliminacji px, a później py. Jeżeli lewy projektor ma zostać nienaruszony, to kolejność eliminacji jest następująca:
Znając wartości pomierzonych paralaks py w sześciu punktach można ułożyć 6 równań dla 5 elementów orientacji, które zostaną wykorzystane do ustawienia na podziałkach autografu. Po ustawieniu obliczonych wartości na przyrządzie dokonuje się ponownego pomiaru paralaks i obliczeń poprawek do elementów orientacji.
61. WARUNEK KOMPLAMARNOŚCI
Dwa środki rzutów O1 i O2, pkt przedmiotu A oraz dwa obrazy tego punktu a' i a'' na zdjęciu stereogramu leżą na wspólnej płaszczyźnie - jest to podstawowy warunek orientacji wzajemnej i fotogrametrycznego wcięcia w przód. Warunek ten określa funkcja Fi, która jest iloczynem mieszanym trzech wektorów Fi = B R1i x R2i = 0
Jedno równanie określające komplemarność trzech wektorów B, R1, R2 można zapisać dla każdego punktu przedmiotu.
(rys)
62. PRZYBLIŻONA METODA WYZNACZENIA ELEMENTÓW ORIENTACJI WZAJEMNEJ.
Zakłada się tu że każdy z fotogramów tworzących stereogram jest wychylony o wartości kątowe EOZ ωL, φL, κL, oraz ωP, φP, κP. Tworzy się układ równań dla 6 pkt standardowych znajdujących się na obszarze podwójnego pokrycia. Metodę tę stosuje się dla układu definiowanego przez poziomą bazę, czyli gdy para zdjęć jest niezależna.
Wychodząc z ogólnego równania poprawek, dzięki temu że możemy ustawić współrzędne dla punktów standardowych, równanie upraszcza się . Poprzez kolejne redukcje możemy wyznaczyć EO wzajemnej, ale tylko kątowe.
Metody tej nie stosuje się do wyrafinowanych procedur analityczno-numerycznych. Stosuje się ją, gdy np. wykonujemy pracę na autografie i aby przyspieszyć proces strojenia, gdy pomierzymy paralaksę i ze wzorów wyliczymy EO wzajemnej.
63. ŚCISŁA METODA WYZNACZANIA ELEMENTÓW ORIENTACJI WZAJEMNEJ - METODA SCHUTA
Metodę tę stosuje się, gdy układ zdefiniowany jest tu umownie (BxF')*F''=0 pozornym lewym zdjęciem. Początkowo punkty przestrzeni przedmiotowej powinny znajdować się w płaszczyznach rdzennych (komplementarności). Na początku zakładamy dla lewego zdjęcia, że φ', ω', χ' = 0, poprawki dla współrzędnych tłowych x', x'' = 0, natomiast poprawki dla y', y'' różnią się znakami, a więc redukują się. Niewiadomymi w równaniu są: by, bz i współrzędne x'', y'', z'' będące współrzędnymi promienia rzutującego r'' określonymi pomierzonymi na zdjęciu wspólrzędnymi x'', y'', CK, φ'', ω'', χ''. Dlatego poszukiwanymi niewiadomymi są: by, bz, φ'', ω'', χ''.
Kolejność obliczeń:
Pięć punktów musi być rozmieszczone jak przy punktach standardowych ze względu na pow. krytyczne gdy mamy więcej niż 5 punktów niewiadome (punkt 4) obliczamy wyrównaniem. Równanie błędów rozwiązujemy metodą najmniejszych kwadratów.
64. ORIENTACJA BEZWZGLĘDNA MODELU METODĄ TRANSFORMACJI PRZESTRZENNEJ PRZEZ PODOBIEŃSTWO
Polega ona na przetransformowaniu układu lokalnego (układu współrzędnych modelu) do układu współrzędnych terenowych. Początkiem lokalnego układu współrzędnych jest środek rzutów lewego zdjęcia a oś celowa lewego zdjęcia pokrywa się z osią układu współrzędnych. Zależność między tymi dwoma układami opisana jest wektorami. Wektor x0 opisuje odległość wektorową między układem współrzędnych geodezyjnych a środkiem rzutów układu współrzędnych modelu; wektor xS opisuje położenie punktu w układzie współrzędnych geodezyjnych, a wektor x - w układzie modelu.
Sposób zapisu wcięcia w przód: xS=x0+mRx
Otrzymujemy tu zespół równań z 7 parametrami transformacji x0, y0, z0 (składowe przesunięcia wektora translacji) elementy kątowe φ, ω, χ macierzy obrotu oraz współrzędne zmiany skali m. Może być tak, że współczynnik zmiany skali wzdłuż każdej osi jest inny (mx, my, mz) i wtedy mamy 9 niewiadomych. Aby obliczyć 7 parametrów w sposób ścisły trzeba mieć min 7 obserwacji ??????????????.
Jednak najczęściej stosuje się 3 pełne fotopunkty, z czego można ułożyć 9 równań. Układ poprawek rozwiązujemy metodą najmniejszych kwadratów i w konsekwencji otrzymujemy parametry transformacji przestrzennej. Parametry te otrzymujemy w procesie iteracyjnym. Teraz korzystając z tych równań obliczamy x, y, z, każdego punktu, który nie jest w danym modelu fotopunktem.
66. BUDOWA MODELU METODĄ WIĄZEK.
Pomiar wykonuje się w układzie poziomej bazy. Jest to metoda jednoczesnego wyznaczenia wszystkich niewiadomych. Muszą być znane współrzędne punktów. Im dokładniej są wyznaczone tym maleje liczba iteracji. Wyznaczamy tu elementy orientacji zewnętrznej x0, y0, z0, φ, ω, χ bazując na warunku kolinearności.
67. RODZAJE I ROZMIESZCZENIE PUNKTÓW W PROCESIE BUDOWY SZEREGU LUB BLOKU AEROTRIANGULACJI - FOTOPUNKTY, PUNKTY WIĄŻĄCE PUNKTY KONTROLNE.
Stereogram - para zdjęć umożliwia obserwacje stereoskopowe. Gdy zdjęcia są silnie zbieżne to nie można wykonywać obserwacji (kąt zbieżności > od 15˚)
Stereogram zdjęc lotniczych - położenie punktów standardowych
+3 +4
+1 +2
+5 +6
12 - baza
12=15=24=26=a' powinna być jak największa aby maksymalnie opisać obszar podwójnego pokrycia
Punkty okołostandardowe - są w obszarze (1 - 1,5 cm) wokół punktów standardowych.
Szereg zdjęć lotniczych
▲Punkty dowiązania (fotopunkty) sygnalizowane w terenie:
na obszarze lotu rozmieszczone co 2 bazy
1) Punkty wyszukiwane przed nalotem i przyjęte do geodezyjnego i fotogrametrycznego wyznaczenia (np. właz do kanału, trójmiedza, pojedynczy krzak, przecięcie dróg polnych)
punkty nawiązania - są o klasę wyżej niż punkty które wyznaczają (dla celów gospodarczych wyznaczamy osnowę III klasy wtedy punkty nawiązania są punktami II klasy)
Punkty wiążące - są w pasach potrójnego pokrycia (obszar wspólny dla 3 kolejnych zdjęć). Muszą być rozmieszczone ~ w środku, u góry i na dole pasa potrójnego pokrycia.
Punkt nowo-wyznaczany - punkty dla których wyznaczane są współrzędne X, Y, Z na drodze fotogrametrycznej ( punkty nowowyznaczanej osnowy III klasy i pomiarowej, punkty katastralne - narożniki działek, punkty sytuacyjne i wysokościowe)
Punkty masowe - były to kiedyś punkty nowowyznaczane.
Punkty kontrolne - punkty, które w procesie rozwiązania i wyrównania areotriangulacji pełnią rolę punktu kontrolnego, są traktowane jako punkty nowo wyznaczane Xgeod - Xfotogr = ∆X (Y analogicznie). Powinny być w najsłabszych miejscach bloku aerotriangulacji (2-3 daleko położone, 1-2 blisko) na obrzeżach lub w środku bloku.
Punkty pomiarowe - wszystkie punkty mierzone w bloku zdjęć fotogrametrycznych.
Punkty standardowe - do numerycznej orientacji wzajemnej pojedynczego modelu.
Technologiczne aspekty wyrównania aerotriangulacji dla bloku zdjęć - rozmieszczenie fotopunktów, wielkość i kształt bloku zdjęć, dokładność wyznaczenia współrzędnych punktów obiektu i elementów orientacji zdjęć.
Metoda Schmida - odpowiada matematycznej realizacji rzutu środkowego. Fotopunkty na obszarze bloku, (jeżeli para zdjęć to 3 fotop. tworzą trójkąt równoboczny).
Dokładność dla metody wiązek (gdy punkty obserwowane są punktami osnowy sygnalizowanej w terenie przed nalotem):
błąd wyanaczenia współrzędnych płaskich:
σ'x,y =6um
σz' = 0,06 %o W-wysokość lotu (SK, WK)
σz' = 0,08 %o W (NSK)
zdjęcia w skali 1:5000
σx,y = 5000x6um
W = MzxCK 300 mm
Wielkość sygnalizowania zależy od
- kąta rozwarcia kamery fotogrametrycznej
Dokładność dla punktów sygnalizowanych naturalnie:
- najdokładniejsze są pokrywy kanałów studzienki /4-6 cm(x,y), 1-3 cm(z)/,
- mniej dokładne są narożniki budynku, płoty /x,y - 7-12 cm, z - 8-15 cm/,
- tereny rolne- narożniki pól /x,y- 20-100 cm, z- 10-20 cm/,
- pojedyncze krzaki, drzewa / x,y- 20-100 cm, z- 20-100 cm/
Błąd długości odcinka w fotogrametrii nie zależu od długości odcinka: ![]()
Metoda niezależnych modeli
- modele są przesunięte, odwrócone i zniekształcone,
- modelem matematycznym rozwiązania jest przestrzenna trassformacja,
- dokładności gorsze niż w metodzie wiązek (plus: jest to metoda etapowa /sekwencyjna/ - 1. orientacja wzajemna, 2. budowa pojedynczego modelu, 3. orientacja bezwzględna; umożliwia rozłączenie wyrównania sieci płaskiej i wysokościowej; minus: występuje problem dołączenia kolejnych modeli).
68. PRZYGOTOWANIE DANYCH FOTOGRAMETRYCZNYCH I GEODEZYJNYCH ORAZ PRZEBIEG ROZWIĄZANIA SZEREGU AEROTRIANGULACJI METODĄ WIĄZEK - NA PRZYKŁADZIE WYRÓWNANIA PROGRAMU AEROSYS.
AeroSys służy do rozwiązania i wyrównania aerotriangulacji metodą wiązek rozwiązanie met. DLT, możliwość samokalibracji, różnych transformacji.
Parametry wejściowe to: współrzędne tłowe w układzie stereokomparatora precyzyjnie zredukowane do punktu głównego; współrzędne fotopunktów i ich dokładności; CK i poprawki kamery dotyczące dystorsji itp; współrzędne znaczków tłowych.
Na początku przygotowujemy pliki: 1. bezename.txt - ze współrzędnymi tłowymi w układzie stereokomparatora. Średnie z wielokrotnego pomiaru, 2. bezename.cal - są tu informacje o: liczbie znaczków tłowych, CK, skalibrowane współrzędne punktu głównego, współrzęne dla określenia dystorsji radialnej, 3. bezename.bdl - plik dzięki któremu program odnajdzie plik tekstowy. Zawiera on: liczbę zdjęć w szeregu, ilość kamer, CK, ilośc znaczków tłowych, 4. bezename.ctl - współrzędne fotopunktów oraz ich dokładności.
Możemy aerotriangulacje obliczyć tu automatycznie lub w sposób etapowy z podglądem. Wynikiem aerotriangulacji są: współrzędne geodezyjne wyrównane nowowyznaczanych punktów; oceny dokładnośći wyznaczenia tych punktów; EOZ; poprawki do obserwacji; wartości średnie dla x, y, z z wyłączeniem lub z włączeniem punktów nawiązania (fotopunktów).
69. AEROTRIANGULACJA METODĄ WIĄZEK
Warunki redukcji do aerotriangulacji:
- w bloku zdjęć odpowiednie punkty dowiązania (fotopunkty). Dla jakości rozwiązania warunkiem koniecznym jest posiadanie punktów nawiązania w narożnikach bloku,
- warunek pokrycia podłużnego szeregu zdjęć (ok 60%), pokrycie poprzeczne 20-30%,
- położenie punktów wiążących (3 pary punktów wiążących w strefak okołostandardowych)
Punkty nowowyznaczane:
punkty wiążące (mogą być to punkty posiłkowe i punkty zagęszczenia osnowy III klasy),
punkty sytuacyjne i wysokościowe numerycznego modelu rzeźby terenu (wyznaczenie punktów osnowy III klasy i punktów osnowy pomiarowej),
punkty sytuacyjne i wysokościowe składające się na mapę numeryczną,
punkty graniczne i punkty załamania granic i punkty określające położenie użytków.
Aerotriangulacja - służy do wyznaczenia współrzędnych przestrzennych punktów (x, y, z) na drodze analitycznej lub analityczno - numerycznej na podstawie pomierzonych na zdjęciu współrzędnych tłowych. Punkty te będą punktami zagęszczenia osnowy III klasy lub osnowy pomiarowej. Jednocześnie służy do wyznaczenia punktów dowiązania w procesie orientacji bezwzględnej modelu.
Punkty nowowyznaczane po rozwiązaniu aerotriangulacji stają się fotopunktami wykorzystywanymi w procesie opracowania zdjęć na autografach.
Na podstawie pojedynczego zdjęcia:
Cechy metody wiązek:
Minusy:
- problem nieliniowości (trzeba linearyzować równania poprawek)
- wymaga pracochłonnych metod obliczeń wartości przybliżonych dla wszystkich niewiadomych,
- jest to metoda o dużym nakładzie obliczeń,
- stanowi rozwiązanie przestrzenne, a więc nie jest możliwe rozdzielenie wyrównania sytuacyjnego i wysokościowego.
Plusy:
70. METODA WIĄZEK Z DODATKOWYMI OBSERWACJAMI I GPS
Obserwacjami dodatkowymi mogą być kąty zenitalne, azymuty, odcinki, kąty poziome, obserwacje fikcyjne, proste pionowe, poziome, dowolnie zorientowane. Można dodatkowo też ułożyć równania ppoprawek do liniowych i kątowych EOZ i EOW.
Równania błędów do tych obserwacji można zapisać w postaci macierzowej i dołączyć do wyrównania metodą najmniejszych kwadratów (pośredniczącą).
Można też dołączyć obserwacje GPS -> współrzędne środków rzutów zdjęć. Jednak nie są one bezbłędne, gdyż w związku z ruchem samolotu są niewielkie rozbieżności pomiędzy rzeczywistymi a rejestrowanymi współrzędnymi GPS. W związku z tym również podlegają one wyrównaniu.
Zarówno obserwacje geodezyjne jak i fotogrametryczne i GPS otrzymują odpowiednie wagi w procesie wyrównania. Obserwacje GPS do nawigacji kamery (samolotu), wyznacają środek rzutów ?????????????????
Obserwacje dodatkowe to dołączenie obserwacji z GPS
I - obserwacje fotogrametryczne - z warunku kolinearności mamy wielkości bezpośrednio obsrewowane czyli 2 współrzędne tłowe każdego punktu pomiarowego.
II - obserwacje geodezyjne - obserwacje fotopunktów, pomierzone odcinki między punktami, azymuty, wysokości
Przy wyrównaniu aerotriangulacji metodą wiązek możemy dołączyć wektor dodatkowy parametrów opisujących EOW oraz parametry opisujące deformacje systematyczne na zdjęciu (dystorsje radialną, tangencjalną, spiralną, ∆x', ∆y', ∆CK).
Dokładność wyznaczenia współrzędnych z samokalibracją:
m'x,y = ± 3um
m'z = ± 0,03 %o W(sk, wk)
Bez zastosowania samokalibracji wyniki są 2x gorsze.
Technika samokalibracji w wyrównaniu bloku zdjęć.
Stosowanie samokalibracji do zdjęć lotniczych pozwala poprawić dokładność opracowania. Potrzeba tu sieci fotopunktów o dużej gęstości i dokładności. Fotopunkty muszą występować na krawędziach bloku, jak i w środku, preferowane jest duże pokrycie poprzeczne, przez co zwiększa się liczba obserwacji nadliczbowych. Jeśli wprowadzimy wielomiany n-tego rzędu ze zbyt dużą liczbą parametrów, to możemy prze parametryzować układ i wówczas spadnie dokładność. Dla każdego fotopunktu możemy otrzymać dodatkowe równanie, mierząc odległości między punktami, kąty, azymuty, obserwacje GPS.
72. AUTOGRAFY ANALITYCZNE - BUDOWA I ZASADA DZIAŁANIA.
Autografy analityczne - autografy precyzyjne, brak ograniczeń spowodowanych paramertami technicznymi instrumentu, realizowana jest projekcja numeryczna.
Budowa:
Systemy obserwacji modelu: binokularny optyczny system obserwacji przestrzennej, 2 rzeczywiste (1 przestrzenny znaczek pomiarowy).
System pomiarowy:
- wprowadzenie danych x: korby ręczne, tarcza nożna, mysz,
- A/D przetwornik (JGR, koder liniowy, tablet
79. NUMERYCZNY MODEL TERENU NMT - PRZEDMIOT I ZAKRES OPRACOWANIA.
NMT - zbiór współrzędnych obrazujących powierzchnię terenu z określoną metodyką obliczeń niezbędną do przetworzenia tych danych. Zbiór wszystkich informacji tworzących NMT przechowuje się w pamięci maszyny lub na odpowiednich nośniku informacji pozwalających na wprowadzenie ich do pamięci.
Punkty, które służą do odtworzenia terenu rozmieszczone są w wybranych punktach charakterystycznych terenu albo leżą na charakterystycznych liniach terenowych (warstwicach, największego spadku, skarpach, itp.) lub też mogą znajdować się w węzłach regularnych siatek.
Na podstawie NMT można rozwiązywać następujące zadania pomiarowe:
- obliczenie wysokości z punktu o zadanym położeniu (x,y),
- obliczenie współrzędnych punktów przekrojów,
- obliczenie objętości bryły ograniczonej powierzchnią terenu i płaszczyznami o danych równaniach,
- obliczenie współrzędnych punktów przebicia powierzchni terenu przez prostą o danym równaniu,
- odliczenie współrzędnych X, Y położenia punktów na warstwicy i określać warstwice
Wyróżniamy NMT rzeźby terenu i NMT sytuacji.
80. NMT - METODA ANALITYCZNA.
Metoda pomiaru:
- regularna siatka kwadratów (oczka rostra zależą od deniwelacji terenu),
- przekroje (x lub y stałe).
Pomiar statyczny rastra i profili (np. wzdłuż określonego azymutu).
Pomiar dynamiczny: np. warstwic, profilowanie dynamiczne.
Zamierzone współrzędne poddano wyrównaniu metodą wiązek.
Interpolacja warstwic i wykreowanie NMT sytuacji dla punktów sygnalizowanych:
σ'x,y =6um
σz' = 0,06 %o W-wysokość lotu (SK, WK)
σz' = 0,08 %o W (NSK)
dochodzi błąd identyfikacji:
łącznie ![]()
![]()
szacunkowe:
pomiar dynamiczny: σz = ±0,25%o W
pomiar statyczny: σz = 0,1 - 0,15 %o W
Fotopumkty - na obrzezach lotu powinny być rozmieszczone co dwie bazy czyli co 2 szeregi. Stosuje się zasade lokalizacji ich w gniazdach. Fotopunkty zawsze zaznaczone na lewym zdjeciu. Sa to punkty osnowy drugiej klasy o znanych wsp. Geodezyjnych (x,y,z)F , P(x,y), Z
Punkty wiazace - min. 3 w pasie potrojnego pokrycia czyli min. 9 procz 1, 2, n-1, n zdjecia w szeregu. Sluzy do powiazania poszczegolnych ukladow.
Punkty nowo wyznaczane - musi być wizura miedzy nimi oraz zachowane odleglosci. Punkty osnowy geod. Widziane z gory na min. 2 kolejnych zdjeciach. Wyznaczamy tu wspol x,y,z metoda fotogrametryczna.
Punkty kontrolne - fotopunkty traktowane jako punkty nowo wyznaczane umieszcz się je w tych miejscach gdzie spodziewamy się najwiekdzych bledow, na obrzezach lub w srodku bloku
Punkty masowe - często się z nich rezygnuje i dopiero w procesie obserwacji tworzy się je wcieciami. Sa to punkty szczegolow sytuacyjnych.
****************************************************
Barwy addytywne, subtraktywne , komplementarne. ADDYTYWNE tworzenie barw : światła o barwach podstawowych są rzutowane i mieszane na wspólnym białym ekranie , tworzą nowe barwy
Filtr |
Barwy |
Nowy kolor |
B G R |
G+R B+R B+G |
Yellow = W-B Magenta = W-G Cyan = W-R |
SUBTRAKTYWNE tworzenie barw : odejmowanie składanych świateł barwnych od światła białego tak, aby otrzymać
W - Y = B W - M = G W - C = R |
B + Y = W G + M = W R + C = W
Y + M + C = Black |
KOMPLEMENTARNE tworzenie barw ( uzupełniające ):
W = Y + B
W = M + G
W = C + R
W = B + G + R
K = C + M + Y
Wyszukiwarka