Opracowanie:

Teresa Malik

Gimnazjum w Rybnej

Jak stosuję czynnościowe nauczanie matematyki w mojej pracy w gimnazjum?

Matematyka- ^..to w mniejszym stopniu wiedzieć, co umieć działać

Servais

Z teorii czynnościowego nauczania

Rozwój myślenia zaczyna się od czynności konkretnych, od działania w rzeczywistości materialnej. Interioryzacja czynności konkretnej prowadzi do czynności wyobrażeniowej. Dziecko może już wykonywać pewne czynności w myśli, ale związane są one ściśle z konkretną sytuacją. Proces interioryzacji prowadzi dalej do myślenia abstrakcyjnymi operacjami. Operacje są to czynności umysłowe już niezależnie od działań wykonywanych na przedmiotach.

Świadome organizowanie sytuacji sprzyjających procesowi interioryzacji to jedna z zasad koncepcji czynnościowego nauczania matematyki. Podczas przygotowania propozycji opracowania danego pojęcia w sposób czynnościowy należy zaplanować takie ćwiczenia. które pozwolą uczniowi przebyć drogę od czynności konkretnych, poprzez wyobrażone do abstrakcyjnych. Myślenie matematyczne to specyficzne działanie, to „świadome posługiwanie się stopniowo przyswajanymi operacjami” (1). Operacje te są rezultatem długiego rozwoju myśli dziecka.

Stosowanie metody czynnościowej w procesie planowania procesu kształtowania pojęć matematycznych powinno polegać na kolejnym przejściu trzech etapów pracy:

etap I - Analiza teoretyczna czynności istotnych dla nowego pojęcia.

Najpierw nauczyciel musi sobie uświadomić, jaki ciąg czynności i w jakiej kolejności należy przeprowadzić, aby skonstruować nowe pojecie. Musi dokonać matematycznej analizy operacji tkwiących w tym pojęciu.

etap II - Ogólny plan kształtowania nowego pojęcia.

Aby pojecie zostało prawidłowo i w pełni przyswojone przez dziecko, należy mieć na uwadze przechodzenie dziecka przez kolejne stada rozwoju intelektualnego: przedoperacyjne, operacji konkretnych i operacji formalnych. W każdym stadium procesowi nauczania mają odpowiadać innego rodzaju ćwiczenia.

etap III- Dobór zadań.

W zależności od poziomu nauczania, na którym nauczyciel kształtuje dane pojęcie, musi on dobrać konkretne zadania, prowadzące do pożądanych czynności ucznia.

Dobór zadań jest niezwykle ważny. „Uczeń tworzy sobie taką koncepcję matematyki, jaka mu się ukazuje przez pryzmat rozwiązywanych przez niego zadań” (1).

W metodzie czynnościowej stosuje się następujące typy ćwiczeń:

1. Ćwiczenia wprost, w których uczeń ma wykonywać prostą czynność lub ciąg czynności.

2. Ćwiczenia odwrotne do poprzednich, wymagające wykonywania czynności lub ciągu czynności odwrotnych do poprzednich.

3. Ćwiczenia tej samej czynności myślowej na różnych materiałach, w różnych położeniach, z zastosowaniem różnych zmiennych, w różnych sytuacjach.

4. Ćwiczenia prowadzące do różnych ciągów czynności o tym samym rezultacie, różne sposoby rozwiązania ,wybór najbardziej ekonomicznej drogi.

5. Ćwiczenia w słownym opisie czynności, konstruowanie planów postępowania opisujących wykonanie czynności.

6. Ćwiczenia prowokujące konflikt myślowy, kontrprzykłady, skrajne przypadki, zadania z błędami uwypuklające istotne warunki definicji i założeń twierdzeń.

7. Ćwiczenia w różnych formach przedstawiania, ilustrowania lub zapisu tego samego zadania, opisy tradycyjne, drzewka, tabele.

Jak stosuję czynnościowe nauczanie matematyki w gimnazjum?

Przy wprowadzaniu nowych pojęć (zwłaszcza w klasach młodszych) organizuję konkretne działania, a nie poprzestaję tylko na pokazie przedmiotów będących ilustracją nowego obiektu. Zamiast wprowadzać wzory i ćwiczyć je w zadaniach, stosuję czynności konkretne. Niektórzy uczniowie wręcz potrzebują czynności konkretnych. Tego typu aktywność jest czasem nieodzowna na moich lekcjach matematyki.

1. Wprowadzanie liczby π.

By przekonać uczniów, ze długość okręgu i długość jego średnicy są wielkościami wprost proporcjonalnymi, odwołuję się do praktycznych ćwiczeń.

Uczniowie przygotowują kilka „okrągłych” przedmiotów, np. monety, puszki, szklanki, a następnie za pomocą nitki, paska papieru lub metra krawieckiego mierzą ich obwód i średnicę. Dzielą długość okręgu przez długość średnicy używając kalkulatorów. Uzupełniają tabelkę i porównują otrzymane wyniki:

Przedmiot	Obwód	Średnica	obwód średnica

2. Objętość ostrosłupa.

Na zadanie domowe polecam uczniom zbudować modele graniastosłupa i ostrosłupa o przystających podstawach i równych wysokościach. Na lekcji uczniowie wypełniają model ostrosłupa piaskiem i przesypują jego zawartość do graniastosłupa. Powtarzają tę czynność tyle razy, by zapełnić graniastosłup. Aby odkryć wzór na objętość ostrosłupa uczniowie sprawdzają ile razy objętość graniastosłupa jest większa od objętości ostrosłupa o takiej samej podstawie i wysokości.

3. Symetria względem prostej.

Na początku uczniowie wykonują ćwiczenia manualne: odbijanie kleksów, przekłuwanie złożonej kartki, wycinanie serwetek, oglądanie rysunku w lusterku. Aby wprowadzić pojęcie osi symetrii polecam uczniom zgiąć kartkę wzdłuż prostej , a następnie wyciąć figurę z podwójnie zgiętej kartki, Tak otrzymane figury mają oś symetrii.

Z kolorowego papieru przygotowuję figury o różnych kształtach. Uczniowie znajdują osie symetrii zginając modele tych figur.

4. Przesunięcie równoległe.

Wprowadzając pojęcie przesunięcia równoległego wykonuję z uczniami następujące ćwiczenia:

• Przykładamy ekierkę do linijki i zaznaczamy końce przeciwprostokątnej. Następnie przesuwamy ekierkę i znów zaznaczamy końce przeciwprostokątnej. W wyniku tego doświadczenia otrzymujemy ilustrację geometryczną przesunięcia równoległego punktu.

• W drugim doświadczeniu rysujemy całą przeciwprostokątną. W ten sposób przesuwamy równolegle odcinek. Kolejne doświadczenia mogą polegać na przesuwaniu innych figur. Mogą to być figury wycięte z kartonu.

5. Wprowadzenie twierdzenia Talesa.

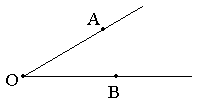
Uczniowie kreślą pewien kąt AOB.

Odkładają na ramieniu OA odcinek OK. o długości 2 cm , a następnie odcinek KL długości 5 cm, na ramieniu OB odcinek OM długości 4 cm. Prowadzą prostą KM, a następnie przez punkt L kreślą prostą równoległą do prostej KM. Oznaczają przez N jej punkt przecięcia z ramieniem OB. Mierzą długość odcinka MN.

Sprawdzają ile razy długość odcinka KL jest większa od długości odcinka OK., a ile razy długość odcinka MN jest większa od długości odcinka OM.

6. Walec.

Uczniowie przygotowują dwie kartki papieru formatu A4. Pierwszą kartkę zwijają w rulon, łącząc ze sobą krótsze boki prostokąta, a drugą zwijają tak by połączyły się krótsze boki. Sprawdzają czy otrzymali powierzchnie boczne takich samych walców. Wyznaczają wymiary przekrojów osiowych obu walców z dokładnością do 1 mm i obliczają ich pola.

Czynności ucznia są związane z modelami figur, z konkretnymi przedmiotami. Uczeń przez manipulowanie dochodzi do istotnych cech pojęcia matematycznego. Czynnościom konkretnym towarzyszą takie aktywności matematyczne jak celowa obserwacja, naśladowanie, dostrzeganie analogii i prawidłowości, schematyzowanie. Konkretne doświadczenie ucznia zostaje intuicyjnie uogólnione, a o to właśnie chodzi w czynnościowym nauczaniu matematyki. To, co uczeń pierwotnie wykonywał konkretnie, będzie wykonywał w myśli.

1. Wiązanie operacji prostych i odwrotnych.

Celowe organizuję dwie przeciwnie skierowane aktywności, wówczas uczeń wykonuje czynności w obu kierunkach.

Przykład:

Wzory zapisujemy w dwóch kierunkach, w dwóch kierunkach je odczytujemy i w dwóch kierunkach stosujemy.

(a + b)² = a² + 2ab + b² i a² + 2ab + b² = (a + b)²

a^{n .} bⁿ = (a ^. b)ⁿ i (a ^. b)ⁿ = a^{n .} bⁿ

Niekiedy stosowanie wzoru „w drugą stronę” wyraźnie ułatwia wykonywanie obliczeń, np. (- 0,2) ^{12 .} 5¹²

Stosowanie wzorów skróconego mnożenia „w drugą stronę” może z kolei usprawnić obliczanie wartości wyrażeń algebraicznych, np. : Oblicz sprytnie wartość wyrażenia : x² + 4x + 4 dla x = 98.

Zmieniając rolę danych z poszukiwanymi, otrzymuję również pary ćwiczeń odwrotnych. Często uczeń rozwiązuje zadania schematycznie. Przy rozwiązywaniu zadania odwrotnego wymagam od ucznia odwrócenia schematu. A to już nie takie łatwe.

Przykłady:

• Ćwiczeniu: „Oblicz pole prostokąta, gdzie dane są długości 4 i 9 jego boków” towarzyszy ćwiczenie: „ Jakie są długości boków prostokąta, którego pole jest równe 36?”. Uczniowie są zaskoczeni tym, że droga odwrotna do tej, którą przebyli poprzednio, nie prowadzi do jednoznacznej odpowiedzi.

• Z zadaniami na obliczanie objętości ostrosłupa powinny być związane zadania typu: „Jaka jest wysokość ostrosłupa o objętości 1dm³ ,jeśli w podstawie jest kwadrat o boku 20 cm.”

• Obliczając z uczniami objętość prostopadłościanu możemy zaproponować im zadanie: „Zaprojektuj pudełko o pojemności 1 litra.

• Z prostym ćwiczeniem, w którym uczeń rysuje wykres danej funkcji liniowej połączymy zadanie: „Wyznacz wzór funkcji, której wykres jest prostą przechodzącą przez punkty A(2,1) i B(-3,-4).”

• Odwrotne rozumowanie potrzebne jest także przy rozwiązywaniu problemu:

„Ułóż treść zadania do układu równań:
.”

Celowo zatem organizuję dwie przeciwnie skierowane czynności - pojęcia matematyczne są wtedy dla uczniów bardziej zrozumiałe i trwalej przyswojone

2. Kontrastowanie.

Na liście zadań kształtujących dane pojęcie umieszczam także kontrprzykłady, które mają na celu kontrastowanie istotnych warunków definicji i twierdzeń.

Oto przykładowe pytania, na które uczeń udzielając odpowiedzi szuka kontrprzykładu, rysując figurę:

1. Definicja osi symetrii figury.

1. Czy osią symetrii figury jest prosta, która dzieli figurę na przystające części?

2. Czy osią symetrii figury jest prosta, która dzieli pole tej figury na połowy?

2. Definicja wielokąta foremnego.

1. Czy prostokąt jest wielokątem foremnym?

2. Czy romb jest wielokątem foremnym?

Uzasadniając odpowiedzi uczeń zwraca uwagę na to, by obydwa warunki definicji były spełnione.

3. Definicja kątów przyległych.

1. Czy kąty przyległe mają być wypukłe, czy to jest warunek konieczny?

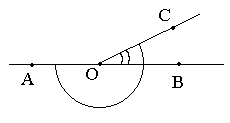
Pytania nauczyciela powinny doprowadzić ucznia do podania rysunkowego kontrprzykładu:

Czy to są kąty przyległe? Który warunek definicji nie jest spełniony?

4. Twierdzenie o stosunku pól figur podobnych.

Zadania wymagające obliczenia obwodu i pola prostokątnej działki o podanych wymiarach oraz podania obwodu i pola działki dwukrotnie większej.

1. Działka ma wymiary 8m x 7m. Ile siatki musisz kupić na jej ogrodzenie?

2. Na jednym metrze kwadratowym (1m²) można posadzić jeden krzak porzeczki. Ile krzaków zmieści się na tej działce?

3. Sąsiad ma działkę o bokach dwa razy dłuższych. Ile siatki potrzebuje na jej ogrodzenie?

4. Ile krzaków porzeczek może zmieścić sąsiad na swojej działce?

Myślę, że jest to dobry przykład wprowadzający ucznia w dosyć trudne twierdzenie.

5) Zadania z błędami.

Stawiam uczniów wobec takich zadań, które wywołują niepokój i prowadzą do dyskusji. W dyskusji uczniowie wyjaśniają, gdzie jest źródło konfliktu.

1. Uczniowie znający twierdzenie Pitagorasa rozwiązują zadanie:

Oblicz wysokość trójkąta o bokach 12cm, 5cm, 5cm.

Niczego nie podejrzewając, kreślą schemat trójkąta i próbują iść przetartym szlakiem. Pojawia się sytuacja konfliktowa. Uczniowie próbują ją wyjaśnić.

2. Dobrym przykładem zadania, w którym także wracamy do nierówności trójkąta może być następujące zadanie:

Obwód trójkąta wynosi 14cm. Długości boków mają się do siebie jak 1:2:4. Oblicz długości boków trójkąta.

3. Rozumienie definicji funkcji sprawdzimy rozwiązując z uczniami zadanie: „Dana jest funkcja, która każdej liczbie całkowitej większej od -2 i mniejszej od 3 przyporządkowuje liczbę do niej odwrotną. Wyznacz zbiór wartości tej funkcji.”

III. Algorytmizacja.

Uczniowie na moich lekcjach poznają matematykę rozwiązując zadania. Posługują się najczęściej schematami i poznanymi algorytmami. Nie zawsze rozumieją sens wykonywanych operacji matematycznych, często nie zastanawiają się nad treścią zadania. Ze względu na dużą ilość algorytmów i pewne podobieństwa między nimi uczniowie zapominają części algorytmu i nie potrafią rozwiązać zadania do końca. Jednak opanowanie podstawowych algorytmów arytmetyki i algebry jest konieczne. Uczniów przyzwyczajam do jasnego i jednoznacznego planowania rozwiązania zadania. Konstruowanie rozwiązań problemów w postaci algorytmów zmusza ich do bardzo ścisłego wyrażania swych myśli.

Klasyczne zadania konstrukcyjne są właśnie takimi problemami, których rozwiązanie przedstawiamy w postaci algorytmu - po analizie zadania i odkryciu sposobu konstrukcji uczniowie sporządzają opis konstrukcji wymieniając kolejne kroki. W ten sposób ukierunkowuję ucznia na informatyczne myślenie.

Algorytmicznie podchodzę do wielu tematów. Oto niektóre z nich:

• podstawowe działania w podzbiorach zbioru liczb rzeczywistych,

• wyznaczanie wartości bezwzględnej liczby,

• zaznaczanie punktu w układzie współrzędnych,

• sporządzanie wykresu funkcji liniowej,

• rozwiązywanie równań i nierówności pierwszego stopnia,

• rozwiązywanie układów równań liniowych metodą wyznaczników,

• rozwiązywanie nierówności liniowej z dwiema niewiadomymi.

IV. Racjonalny wybór schematu.

Czasami rozwiązuję zadanie z uczniami, odrywając się od schematu. Robię to tam gdzie do rozwiązania można dojść różnymi drogami.

1. „W ogrodzie mandaryna były bażanty i króliki. Miały one razem 35 głów i 94 nogi. Ile było bażantów, a ile królików?”

Na ogół uczniowie rozwiązują to zadanie za pomocą układu równań, tymczasem metoda niealgebraiczna jest prostsza. Załóżmy, że wszystkie zwierzęta usiadły na dwóch łapach. Wówczas będą widoczne 94 - 2^.35 = 24 nogi, przy czym będą widoczne jedynie nogi królików. Zatem królików będzie 24 :2 =12, a bażantów 35 - 12 = 23.

2. Oto prosty przykład sprawdzający umiejętność odejmowania pisemnego: „Ile to będzie 10101010 - 9999?” Wykonując to działanie sposobem pisemnym można nie obliczyć tej różnicy za pierwszym podejściem. Tymczasem wystarczy w pamięci odjąć 10000, a następnie dodać 1.

Zakończenie

Metoda czynnościowa pomaga mi w aktywizowaniu ucznia, zachęca do podejmowania działania. Wtedy uczeń zdobywa wiedzę operatywną, ucząc się przez działanie. Jest stroną aktywną na lekcji. Ja pełnię rolę organizatora procesu nauczania, przewodnika, doradcy, wychowawcy - stwarzam warunki do uczenia się. Kładę zatem duży nacisk nie tylko na wiadomości, ale przede wszystkim na umiejętności. Staram się indywidualizować pracę każdego ucznia. Stosuję pracę w grupach, związaną z wykonywaniem doświadczeń i przekazywaniem ich wyników.

Wyjaśnienie:

Przykłady zadań są albo mojego pomysłu, albo pochodzą z różnych zbiorów

i podręczników, albo poznawałam je na różnych formach doskonalenia.

Nie uzurpuję sobie prawa do bycia ich autorem.

PUBLIKACJE CYTOWANE

1.Z.Krygowska,”Zarys dydaktyki matematyki”,cz.1,W-wa 1969, PZWS

1

6

---